Другие задания смотри здесь...
![]()
Задание 351.
35 • 0 < 23 • 1
84 - 0 = 84 • 1
44 • 1 < 44 + 1
45 - 1 < 45 • 1
63 + 0 > 63 • 0
74 • 0 < 74 - 1
Задание 352. В одной корзине а кг винограда, а в другой — в 2 раза меньше. Весь виноград разложили в четыре ящика поровну. Сколько килограммов винограда в одном ящике?
Решение.
а : 2 (кг) – винограда в другом ящике.
а + а : 2 (кг) – весь виноград.
(а + а : 2) : 4 (кг) – винограда в одном ящике.
Ответ: в одном ящике (а + а : 2) : 4 килограмм винограда.
Задание 353. Из 35 кг абрикосов получили 5 кг кураги. Сколько килограммов кураги выйдет из 63 кг абрикосов?
35 кг абрикосов – 5 кг кураги
63 кг абрикосов - ? кг кураги.
Решение.
35 : 5 = 7 (кг) – абрикосов для получения 1 кг кураги.
63 : 7 = 9 (кг) – кураги выйдет.
Ответ: выйдет 9 кг кураги.
Составь подобную задачу по схеме.
□ : (□ : □)
Из 27 кг винограда получили 9 кг изюма. Сколько килограмм изюма выйдет из 63 кг винограда?
Задание 354*. Если каждому своему ребёнку мама даст по 7 конфет, то у неё останется ещё 8 конфет, а если по 9 конфет, то конфет не останется. Сколько конфет у мамы?
Решение.
1 способ.
9 – 7 = 2 (к.) – на столько меньше конфет получит каждый ребёнок, если мама даст по 7 конфет.
8 : 2 = 4 (д.) – количество детей.
9 • 4 = 36 (к.) – конфет у мамы.
2 способ.
Пускай х – количество детей. Тогда 7х (к.) – конфет у всех детей, когда мама дала по 7 шт., 9х (к.) – конфет у всех детей, когда мама дала по 9 шт. Сложим уравнение
9х - 7х = 8
2х = 8
х = 8 : 2
х = 4 (д.) – детей у мамы.
9х = 9 • 4 = 36 (к.) – конфет у мамы.
Ответ: у мамы было 36 конфет.
Задание 355.
64 • 0 + 28 = 28 58 - 34 • 1 = 58 – 34 = 24 24 • 1 • 0 = 0
39 • 1 – 24 = 39 – 24 = 15 (45 + 36) • 0 = 0 72 : 9 • 1 = 8 • 1 = 8
Задание 356. 36 кг макарон расфасовали в 9 одинаковых пакетов. Сколько нужно таких пакетов, чтобы расфасовать ещё 28 кг макарон?
Решение.
36 : 9 = 4 (кг) – масса 1 пакета.
28 : 4 = 7 (п.) – нужно таких пакетов.
Ответ: нужно 7 таких пакетов.
Задание 357. (Устно.)
8 • 1 • 4 = 32 7 • 0 • 6 = 0 3 • 0 + 7 = 7 34 • 1 = 34
6 • 0 + 3 = 3 8 • 4 • 0 = 0 6 • 2 • 1 = 12 34 – 1 = 33
Задание 358. Из каждого выражения на умножение и его значения составь по два равенства с делением.
3 • 7 = 21 4 • 5 = 20 6 • 2 = 12 9 • 4 = 36
21 : 3 = 7 20 : 4 = 5 12 : 6 = 2 36 : 9 = 4
21 : 7 = 3 20 : 5 = 4 12 : 2 = 6 36 : 4 = 9
Задание 359.
4 • 1 = 4 6 • 1 = 6 7 • 1 = 7 3 • 1 = 3
4 : 1 = 4 6 : 1 = 6 7 : 1 = 7 3 : 1 = 3
4 : 4 = 1 6 : 6 = 1 7 : 7 = 1 3 : 3 = 1
Задание 360.
4 • 6 + 18 : 1 = 24 + 18 = 42
4 • 6 - 18 • 1 = 24 - 18 = 6
3 • 7 + 7 : 7 = 21 + 1 = 22
8 : 1 + 6 • 0 = 8 + 0 = 8
8 • 1 - 8 : 8 = 8 - 1 = 7
5 : 5 + 5 • 4 = 1 + 20 = 21
Задание 361. Купили 6 м шёлка, сатина — в 2 раза больше, а сукна — на 3 м меньше, чем шёлка и сатина вместе. Сколько метров сукна купили?
Решение.
6 • 2 = 12 (м) – сатина купили.
6 + 12 = 18 (м) – шёлка и сатина вместе купили.
18 – 3 = 15 (м) – сукна купили.
Ответ: купили 15 м сукна.
Составь обратную задачу, чтобы найти число 3.
Купили 15 м сукна, 6 м шелка, а сатина — в 2 раза больше, чем шелка. На сколько меньше приобрели сукна, чем сатина и шёлка вместе?
Решение.
6 • 2 = 12 (м) – сатина купили.
6 + 12 = 18 (м) – сатина и шелка купили вместе.
18 – 15 = 3 (м) – на столько меньше приобрели сукна, чем сатина и шелка вместе.
Ответ: сукна приобрели на 3 м меньше, чем сатина и шелка вместе.
Задание 362. Составь задачи по кратким записям.

В первом рулоне 4 м ткани. Во втором рулоне ткани у 3 раза больше, чем в первом. В третьем рулоне ткани на 2 м больше, чем во втором рулоне. Сколько ткани в третьем рулоне?
Решение.
В парке растёт 4 берёзы, клёнов у 2 раза больше, чем берёз. Сколько дубов в парке, если их на 3 меньше, чем клёнов?
Задание 363*. Построй прямоугольник, ширина которого в 3 раза меньше длины и равна 2 см. Подели его на три равных квадрата. Сравни периметр этого прямоугольника и полученного квадрата.
Решение.
2 • 3 = 6 (см) – длина большего прямоугольника.
Р1 = (2 см + 6 см) • 2 = 16 см – периметр прямоугольника.
Р2 = 2 см • 4 = 8 см – периметр квадрата.
16 : 8 = 2 (раза) – во столько раз больше периметр прямоугольника, чем квадрата.
16 – 8 (см) – на столько больше периметр прямоугольника, чем квадрата.
Ответ: периметр прямоугольника в 2 раза больше периметра квадрата; периметр прямоугольника на 8 см больше, чем периметр квадрата.
Задание 364. Реши уравнение.
|
45 : х = 1 х = 45 : 1 х = 45 45 : 45 = 1 |
42 : x= 42 х = 42 : 42 х = 1 42 : 1 = 42 |
x : 34 = 1 х = 34 • 1 x= 34 34 : 34 = 1 |
х – 34 = 34 х = 34 + 34 х = 68 68 – 34 = 34 |
|
38 • х = 38 х = 38 : 38 х = 1 38 • 1 = 38 |
36 - х = 1 х = 36 – 1 х = 35 36 – 35 = 1 |
х • 54 = 54 х = 54 : 54 х = 1 1 • 54 = 54 |
24 + х = 24 х = 24 – 24 х = 0 24 + 0 = 24 |
Задание 365. На одном участке растёт 15 кустов сирени, на втором — на 3 куста меньше, а на третьем — в 3 раза меньше, чем на первом и втором вместе. Сколько кустов сирени растёт на третьем участке?
Решение.
15 – 3 = 12 (к.) – кустов сирени на втором участке.
15 + 12 = 27 (к.) – кустов сирени вместе на первом и втором участках.
27 : 3 = 9 (к.) – кустов сирени растёт на третьем участке.
Ответ: на третьем участке растёт 9 кустов сирени.
Задание 366. (Устно.)
0 • 5 • 3 = 0 7 • 0 • 4 = 0 6 • 2 • 0 = 0 8 : 1 • 0 = 0
1 • 0 + 3 = 3 27 : 9 • 0 = 3 • 0 = 0 34 + 8 • 0 = 34 72 : 8 – 0 = 9
Задание 367.
4 • 0 = 0 0 • 7 = 0 8 • 0 = 0
0 : 4 = 0 0 : 7 = 0 0 : 8 = 0
0 : а = 0
Внимание: делить на нуль невозможно!
Задание 368. Составь и вычисли возможные выражения а • b и а : b, если а и b могут приобретать значения: 2, 3, 4, 0, 6, 12.
|
2 • 3 = 6 2 • 4 = 8 2 • 0 = 0 2 • 6 = 12 2 • 12 = 24 3 • 4 = 12 3 • 0 = 0 3 • 6 = 18 3 • 12 = 36 4 • 0 = 0 4 • 6 = 24 4 • 12 = 48 0 • 6 = 0 0 • 12 = 0 6 • 12 = 72 |
4 : 2 = 2 6 : 2 = 3 6 : 3 = 2 12 : 2 = 6 12 : 3 = 4 12 : 4 = 3 12 : 6 = 2
0 : 2 = 0 0 : 3 = 0 0 : 4 = 0 0 : 6 = 0 0 : 12 = 0
|
Задание 369. На одной полке стояло 9 книг, а на второй — в 2 раза больше. Взяли 6 книг с обеих полок. Сколько всего книг осталось на обеих полках? Реши задачу разными способами.
Решение.
1 способ.
9 • 2 = 18 (к.) – книг стояло на второй полке.
9 – 6 = 3 (к.) – книг осталось на первой полке.
18 – 6 = 12 (к.) – книг осталось на второй полке.
12 + 3 = 15 (к.) – книг осталось на обеих полках.
2 способ.
9 • 2 = 18 (к.) – книг стояло на второй полке.
9 + 18 = 27 (к.) – книг стояло на двух полках.
6 • 2 = 12 (к.) – книг забрали с обеих полок.
27 – 12 = 15 (к.) – книг осталось на обеих полках.
Ответ: на обеих полках осталось 15 книг.
Задание 370. 1) Составь и реши задачи и сравни их.
а) I — 16 м
II — на 8 м меньше
III — ?, в 4 раза меньше, чем I и II вместе
Первой швее дали 16 м ткани, второй швее – на 8 м меньше, чем первой. Сколько метров ткани получила третья швея, если ей дали ткани в 4 раза меньше, чем первой и второй швее вместе?
Решение.
16 – 8 = 8 (м) – ткани получила вторая швея.
16 + 8 = 24 (м) – ткани получили первая и вторая швея вместе.
24 : 4 = 6 (м) – метров ткани получила третья швея.
Ответ: третья швея получила 6 м ткани.
б) I — 16 м
II — в 8 раз меньше
III — ?, на 4 м меньше, чем I и II вместе
Первой швее дали 16 м ткани, второй швее – в 8 м меньше, чем первой. Сколько метров ткани получила третья швея, если ей дали ткани на 4 м меньше, чем первой и второй швее вместе?
Решение.
16 : 8 = 2 (м) – ткани дали второй швее.
16 + 2 = 18 (м) – ткани дали первой и второй швее вместе.
18 – 4 = 14 (м) – ткани получила третья швея.
Ответ: третья швея получила 14 м ткани.
2) Составь задачи о птицах-долгожителях по таблице.
|
Птица |
Максимальная продолжительность жизни |
|
Кондор |
80 лет |
|
Беркут |
80 лет |
|
Ворон |
70 лет |
|
Страус |
50 лет |
|
Лебедь |
25 лет |
|
Дрозд |
20 лет |
Решение.
Птица кондор живёт 80 лет, а дрозд 20 лет. На сколько больше лет живет кондор, чем дрозд?
Кондор и беркут живут по 80 лет, ворон живёт 70 лет. Сколько вместе лет живут кондор, беркут и ворон?
Кондор живёт 80 лет, лебедь – 25 лет, дрозд – 20 лет. На сколько лет меньше живут лебедь и дрозд вместе, чем кондор?
Страус живёт 50 лет, а лебедь – 25 лет. На сколько лет больше живёт страус?
Задание 371*. На двух кустах сидело 10 воробьёв. После того как на первый прилетело ещё 5 воробьёв, а на второй — ещё 3, на обоих кустах воробьёв стало поровну. Сколько воробьёв было на каждом кусте сначала?
Решение.
10 + (5 + 3) = 18 (в.) – воробьёв стало всего.
18 : 2 = 9 (в.) – воробьёв стало на каждом кусте.
9 – 5 = 4 (в.) – воробьёв было сначала на первом кусте.
9 – 3 = 6 (в.) – воробьёв было на втором кусте.
Ответ: сначала было на первом кусте 4 воробья, на втором – 6 воробьёв.
Задание 372.
54 : 9 • 0 = 0 54 - 9 • 0 = 54 (36 + 0) • 1 = 36
42 • 0 : 7 42 • (0 : 7) = 0 (36 + 1) • 0 = 0
Задание 373°. В одну вазу поставили 15 цветков, во вторую — в 3 раза меньше, а в третью — на 4 цветка больше, чем во вторую. Сколько всего цветков в трёх вазах?
15 : 3 = 5 (ц.) – цветка во второй вазе.
5 + 4 = 9 (ц.) – цветков в третьей вазе.
15 + 5 + 9 = 29 (ц.) – цветков в трёх вазах.
Ответ: в трёх вазах 29 цветков.
Дополнительные упражнения
Упражнение 1. Запиши все двузначные числа, в которых количество десятков и количество единиц отличается на 2.
20, 31, 42, 53, 64, 75, 86, 97, 13, 24, 35, 46, 57, 68, 79
Упражнение 2. Запиши все двузначные числа, в которых сумма количества десятков и количества единиц равна 9.
18, 27, 36, 45, 54, 63, 72, 81, 90
Упражнение 3. Восстанови равенства, подобрав числа и знаки.
|
9 • □ = 18 9 • □ = 72 |
81 □ □ = 9 81 □ □ = 72 |
4 • □ + 8 = 28 (18 + □) : 4 = 5 |
9 • 2 = 18
9 • 8 = 72
81 : 9 = 9
81 - 9 = 72
4 • 5 + 8 = 28
(18 + 2) : 4 = 5
Упражнение 4. Запиши последовательно выражения, чтобы достичь вершины пирамиды: число вверху является суммой двух чисел под ним.
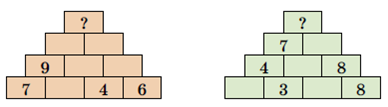
Решение.
|
|
|
|
31 |
|
|
|
|
|
|
|
15 |
16 |
|
|
||
|
|
9 |
6 |
10 |
|
|||
|
7 |
2 |
4 |
6 |
||||
|
|
|
|
|
|
|
|
|
|
|
|
|
17 |
|
|
|
|
|
|
|
7 |
11 |
|
|
||
|
|
4 |
3 |
8 |
|
|||
|
1 |
3 |
1 |
8 |
||||
|
|
|
|
|
|
|
|
|
Упражнение 5. Весенние каникулы начались 24 марта и закончились 31 марта. Сколько дней они длились?
31 – 24 + 1 = 8 (д.) – дней длились каникулы.
Упражнение 6. Вика начала утреннюю зарядку в 7 ч 30 мин и закончила через 15 мин. У котором часу девочка закончила зарядку?
7 ч 30 мин + 15 ми = 7 ч + (30 мин + 15 мин) = 7 ч + 45 мин.
Упражнение 7. Полёт первого лётчика-космонавта Юрия Гагарина начался в 9 ч 7 мин, а закончился в 10 ч 55 мин. Сколько времени длился полёт?
1 способ.
10 ч 55 мин – 9 ч 7 мин = (10 ч – 9 ч) + (55 мин – 7 мин) = 1 ч 48 мин.
2 способ.
_10 ч 55 мин
9 ч 07 мин
1 ч 48 мин
Упражнение 8. Посеяли 9 кг гороха, а собрали на 36 кг больше. Во сколько раз больше собрали гороха, чем посеяли?
Решение.
9 + 36 = 45 (кг) – гороха собрали.
45 : 9 = 5 (раз) – во столько раз больше собрали гороха, чем посеяли.
Ответ: собрали в 5 раз больше гороха, чем посеяли.
Упражнение 9. Бобёр может не дышать под водой 15 мин, а кашалот — в 4 раза дольше. На сколько больше времени может находиться под водой кашалот, чем бобёр?
Решение.
15 • 4 = (10 + 5) • 4 = 40 + 20 = 60 (мин) – столько времени может находиться под водой кашалот.
60 – 15 = 45 (мин) – на столько времени больше может находиться под водой кашалот, чем бобер.
Ответ: кашалот может находиться под водой на 45 минут больше, чем бобёр.
Упражнение 10. В одном пансионате отдыхало а человек, а в другом — в 4 раза больше. На сколько меньше человек отдыхало в первом пансионате, чем во втором?
Решение.
а • 4 (чел.) – человек отдыхало в другом пансионате.
а • 4 – а (чел.) – на столько меньше человек отдыхало в одном пансионате, чем в другом.
Ответ: в одном пансионате отдыхало на а • 4 – а человек меньше, чем в другом.
Упражнение 11.
|
28 : х = 7 х = 28 : 7 х = 4 28 : 4 = 7 |
х : 6 = 9 х = 9 • 6 х = 54 54 : 6 = 9 |
9 • х = 63 х = 63 : 9 х = 7 9 • 7 = 63 |
|
28 – х = 7 х = 28 – 7 х = 14 28 – 14 = 7 |
х – 6 = 9 х = 9 + 6 х = 15 15 – 6 = 9 |
9 + х = 63 х = 63 – 9 х = 54 9 + 54 = 63 |
Упражнение 12. В первый день выставку детских рисунков посетили а человек, что в 2 раза меньше, чем во второй день. Сколько всего человек посетило выставку за два дня?
Решение.
а • 2 (чел.) – человек посетили выставку во второй день.
а + а • 2 (чел.) – человек посетили выставку за два дня.
Ответ: за два дня выставку посетило а + а • 2 человек.
Упражнение 13. По блок-схемам составь и вычисли выражения.
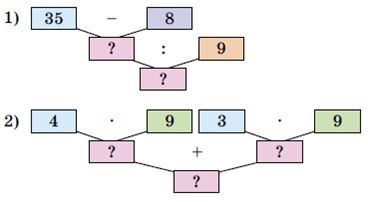
1) (35 – 8) : 3 = 27 : 3 = 9
2) (4 • 9) + (3 • 9) = 36 + 27 = 63
Упражнение 14. По рисунку выпиши множество: 1) Треугольников. 2) Четырёхугольников. 3) Квадратов.
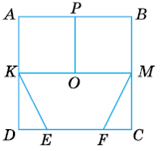
1) DKE, FMC.
2) KAPO. OPBM. KABP. DKMC, DABC.
3) KAPO, OPBM, DAPC.