Другие задания смотри здесь...
![]()
Задание 751. Из произведений составь равенства с делением на 100 и сделай вывод.
4 • 100 = 400 6 • 100 = □ 8 • 100 = □
400 : 100 = 4 600 : 100 = □ □ : 100 = □
Розв'язання:
4 • 100 = 400 6 • 100 = 600 8 • 100 = 800
400 : 100 = 4 600 : 100 = 6 800 : 100 = 8
Чтобы разделить на 100 число, которое заканчивается нулями, надо в нём справа закрыть два нуля.
Задание 752.
80 • 10 : 100 = 800 : 100 = 8
900 : 10 : 10 = 90 : 10 = 9
100 • 5 : 10 = 500 : 10 = 50
100 • 7 : 10 = 700 : 10 = 70
60 – 100 : 100 =60 – 1 = 59
1 • 1 • 1 + 100 = 1 + 100 = 101
Задание 753. Спортсмен пробежал на коньках 1000 м за 1 мин 40 с. Сколько метров в секунду он пробегал?
Решение.
1 мин 40 с = 1 • 60 с + 40 с = 100 с, тогда
1000 : 100 = 10 (м) – расстояние за секунду пробежал.
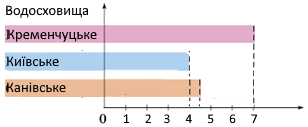
Задание 754. (Устно.) Используя диаграмму продолжительности жизни животных, составь и реши задачи.
Собака живёт 24 года, а мышь – 2 года. На сколько дольше живёт собака, чем мышь?
Решение.
24 – 2 = 22 (года) – на столько дольше живёт собака, чем мышь.
Ответ: собака живёт на 22 года дольше, чем мышь.
Шпак живёт 12 лет, а мышь – 2 года. Во сколько раз дольше живёт шпак?
Решение.
12 : 2 = 6 (раз) – во столько раз дольше живёт шпак, чем мышь.
Ответ: шпак живёт у 6 раз дольше, чем мышь.
Задание 755*. Рыбак поймал щуку, которая весит 2 кг и ещё треть своей массы. Какова масса щуки?
Решение.
1 способ.
Поскольку щука составляет три части, а две части весят 2 кг, тогда
2 : 2 = 1 (кг) – весит одна часть.
1 • 3 = 3 (кг) – весит щука (3 части).
2 способ.
Поскольку 2/3 щуки уже составляет 2 кг, тогда
2 : 2 • 3 = 3 (кг) – весит щука.
Ответ: масса щуки 3 кг.
Задание 756°.
5 • 2 • 10 = 10 • 10 = 100
600 : 100 = 6
60 : 10 = 6
500 : 100 = 5
100 • 7 • 1 = 700
6 • 100 : 1 = 600
63 – 9 • 7 : 1 = 63 – 63 = 0
(63 – 9) : 9 = 54 : 9 = 6
Задание 757°. Зимой легковой автомобиль на 1 км пути расходует 87 г бензина, а летом — 80 г. На сколько грамм бензина меньше расходует автомобиль летом на 100 км пути, чем зимой?
Решение.
1 способ.
87 – 80 = 7 (г) – на столько меньше бензина израсходует летом на 1 км пути.
7 • 100 = 700 (г) – на столько меньше бензина израсходует летом на 100 км пути.
2 способ.
87 • 100 = 8700 (г) – бензина израсходует на 100 км зимой.
80 • 100 = 8000 (г) – бензина израсходует на 100 км летом.
8700 – 8000 = 700 (г) – на столько меньше бензина израсходует летом на 100 км пути.
Ответ: на 100 км пути летом автомобиль израсходует на 700 г меньше бензина, чем зимой.
Умножение и деление разрядных чисел на однозначное число
Задание 758. (Устно.)
5 : 5 + 5 = 6 100 : 10 + 10 = 20 0 • 6 + 4 = 4
100 • 1 + 0 = 100 900 : 10 – 1 = 89 8 : 8 – 1 = 0
Задание 759. Пользуясь образцом, найди частные и объясни способ вычисления.
80 : 8 = 10 700 : 7 = 100
8 дес. : 8 = 1 дес.7 сот. : 7 = 1 сот.
Решение.
90 : 9 = 10
9 дес. : 9 = 1 дес.
40 : 4 = 10
4 дес. : 4 = 1 дес.
600 : 6 = 100
6 сот. : 6 = 1 сот.
500 : 10 = 50
5 сот. : 1 дес. = 5 дес.
Задание 760. Из 24 кг сахарной свёклы получили 4 кг сахара. Сколько килограммов сахара можно получить из 600 кг такой свёклы?
Решение.
24 кг свёклы – 4 кг сахара.
600 кг свёклы – ? кг сахара.
24 : 4 = 6 (раз) – у столько раз меньше сахара получится.
600 : 6 = 100 (кг) – сахара можно получить.
Ответ: из 600 кг свёклы можно получить 100 г сахара.
Составь обратную задачу, чтобы найти число 600.
Из 24 кг сахарной свёклы получили 4 кг сахара. Сколько килограммов свёклы надо взять, чтобы получить 100 кг сахара?
Решение.
24 кг свёклы – 4 кг сахара.
? кг свёклы – 600 кг сахара.
24 : 4 = 6 (раз) – у столько раз больше свёклы надо взять.
100 • 6 = 600 (кг) – свёклы надо взять.
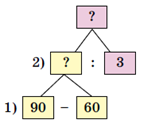
Задание 761. В швейной мастерской было 90 м шёлка. Когда сшили несколько платьев, расходуя на каждое по 3 м, то осталось ещё 60 м. Сколько сшили платьев? По схеме составь план решения и запиши решение.
Решение.
90 – 60 = 30 (м) – шёлка использовали на платья.
30 : 3 = 10 (п.) – платьев сшили.
Ответ: сшили 10 платьев.
Задание 762. Запиши в виде равенств такие утверждения.
1) Число 680 меньше числа а на 140.
2) Число b больше числа 6 в 3 раза.
Решение.
|
1) 680 – а = 140 а + 140 = 680 680 + 140 = а |
2) b : 6 = 3 b : 3 = 6 6 • 3 = b |
Задание 763*. В трёх пакетах было поровну орехов. Когда из каждого пакета взяли по 6 орехов, то в них стало столько орехов, сколько было раньше в двух пакетах. Сколько орехов было в каждом пакете сначала?
Решение.
1 способ.
Пускай х (ор.) – орехов в одном пакете, тогда х – 6 (ор.) – орехов стало в каждом пакете. Составим уравнение:
3 • (х – 6) = 2х
3х – 18 = 2х
3х – 2х = 18
х = 18 (ор.) – орехов в каждом пакете сначала.
2 способ.
6 • 3 = 18 (ор.) – орехов взяли всего (орехов в третьем пакете).
Ответ: в каждом пакете было 18 орехов.
Задание 764.
(37 + 33) : 10 = 70 : 10 = 7
(37 + 13) : 5 = 50 : 5 = 10
50 – 20 : 5 = 50 – 4 = 46
50 – 20 : 10 = 50 – 2 = 48
(50 – 20) : 10 = 30 : 10 = 3
500 – 200 : 2 = 500 – 100 = 400
Задание 765. В магазин привезли 100 кг муки. 80 кг муки было в мешке, остальная — в пакетах, по 2 кг в каждом. Сколько было пакетов с мукой?
Решение.
100 – 80 = 20 (кг) – муки в пакетах.
20 : 2 = 10 (п.) – пакетов с мукой.
Ответ: было 10 пакетов с мукой.
Задание 766. Замени числа произведениями по образцам.
30 = 3 • 10
300 = 3 • 100
60 = 6 • 10
90 = 9 • 10
700 = 7 • 100
500 = 5 • 100
Задание 767. Используя законы умножения, найди произведения удобными способами.
4 • 10 • 3 = (4 • 3) • 10 = 12 • 10 = 120
6 • 5 • 10 = 30 • 10 = 300
2 • 100 • 3 = (2 • 3) • 100 = 6 • 100 = 600
100 • 4 • 2 = 100 • (4 • 2) = 100 • 8 = 800
Задание 768. Объясни, как находили произведения и частные.
30 • 3 = 90
3 дес. • 3 = 9 дес.
200 • 4 = 800
2 сот. • 4 = 8 сот.
60 : 3 = 20
6 дес. : 3 = 2 дес.
900 : 3 = 300
9 сот. : 3 = 3 сот.
Задание 769. Два ученика по-разному нашли произведение 3 • 20. Объясни, как рассуждал каждый из них.
Решение.
1-й ученик: 3 • 20 = 20 • 3 = 60 (переместительный закон умножения).
2-й ученик: 3 • 20 = 3 • 2 • 10 = 6 • 10 = 60 (сочетательный закон умножения).
Задание 770. (Устно.)
2 • 4 = 8 9 : 3 = 3 10 : 2 = 5 5 • 2 = 10
20 • 4 = 80 90 : 3 = 30 100 : 2 = 50 50 • 2 = 100
200 • 4 = 800 900 : 3 = 300 1000 : 2 = 500 500 • 2 = 1000
Заданий 771.
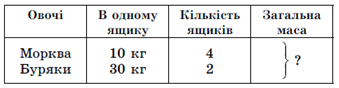
В магазин завезли 4 ящика моркови по 10 кг в каждом ящике, 2 ящика свёклы по 30 кг в каждом ящике. Общая масса овощей?
Решение.
10 • 4 = 40 (кг) – масса моркови.
30 • 2 = 60 (кг) – масса свёклы.
40 + 60 = 100 (кг) – общая масса овощей.
Ответ: общая масса овощей 100 кг.
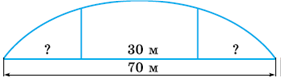
Задание 772. Через реку построен мост длиной 70 м. У него 3 прогона. Длина среднего прогона 30 м. Найди длину крайних прогонов, если они равны между собой.
Решение.
70 – 30 = 40 (м) – длина двух крайних прогонов вместе.
40 : 2 = 20 (м) – длина крайнего прогона.
Ответ: длина крайнего прогона 20 м.
Измени вопрос, чтобы в решении добавилось ещё одно действие.
Во сколько раз длина крайнего прогона меньше, чем среднего.
Решение.
70 – 30 = 40 (м) – длина двух крайних прогонов вместе.
40 : 2 = 20 (м) – длина крайнего прогона.
40 : 20 = 2 (раза) – во столько раз меньше длина крайнего прогона, чем среднего.
Ответ: длина крайнего прогона у 2 раза меньше, чем среднего.
Задание 773.
|
х • 4 = 800 х = 800 : 4 х = 200 200 • 4 = 800 |
600 : x = 100 х = 600 : 100 х = 6 600 : 6 = 100 |
x : 3 = 200 х = 200 • 3 х = 600 600 : 3 = 200 |
Задание 774*. Найди сумму всех трёхзначных чисел, сумма цифр в записях которых равна 3.
Решение.
102, 120, 111, 201, 210, 300
102 + 120 + 111 + 201 + 210 + 300 = (102 + 111 + 201) + (300 + 120 + 210) =
= 414 + 630 = (400 + 600) + (14 + 30) = 1044
Задание 775. Взрослый прошёл на лыжах 900 м за 3 мин, а мальчик — 400 м за 2 мин. На сколько больше метров проходил за 1 мин взрослый, чем мальчик?
Решение.
900 : 3 = 300 (м) – расстояние взрослого за 1 мин.
400 : 2 = 200 (м) – расстояние мальчика за 1 мин.
300 – 200 = 100 (м) – на столько больше метров за 1 мин прошёл взрослый, чем мальчик.
Ответ: взрослый за 1 мин проходил на 100 м больше, чем мальчик.