ГДЗ Ответы Математика 3 класс Богданович М В, Лишенко Г П 851 – 875 задания, 133

Задание 851.

Делимое	28	80			6	60	100	90
Делитель	4	40	12	20			5
Частное			5	5	3	30		30

Решение.

Делимое	28	80	12 • 5 = 60	20 • 5 = 100	6	60	100	90
Делитель	4	40	12	20	6 : 3 = 2	60 : 30 = 2	5	90 : 30 = 3
Частное	28 : 4 = 7	80 : 40 =2	5	5	3	30	100 : 5 = 20	30

Задание 852. Рассмотри записи и объясни способ вычисления.

70 • 8 = 560

7 дес. • 8 = 56 дес.

420 : 6 = 70

42 дес. : 6 = 7 дес.

Задание 853. (Устно.)

30 • 8 = 240

90 • 3 = 270

640 : 8 = 80

350 : 7 = 50

120 : 6 • 5 = 100

400 : 5 : 10 = 8

240 – 180 : 3 = 180

540 + 60 • 6 = 900

Задание 854. Посеяли 60 кг проса, ячменя — в 3 раза меньше, чем проса, а кукурузы — в 2 раза больше, чем ячменя и проса вместе. Сколько посеяли кукурузы?

Решение.

60 : 3 = 20 (кг) – ячменя посеяли.

60 + 20 = 80 (кг) – вместе ячменя и проса посеяли.

80 • 2 = 160 (кг) – кукурузы посеяли.

Ответ: посеяли 160 кг кукурузы.

Задание 855. Запиши все значения буквы х, при которых неравенства истинны.

1) х - 20 < 7;

Решим уравнение

х – 20 = 7

х = 7 + 20

х = 27

27 – 20 = 7

Тогда можно записать

х – 20 < 27 – 20

Разность меньше, если уменьшаемое меньше

х < 27

2) 15 - х > 10

Решим уравнение

15 – х = 10

х = 15 – 10

х = 5

15 – 5 = 10

Тогда можно записать

15 – х > 15 – 5

Разность больше, если вычитаемое меньше

х < 5

3) х • 3 < 20.

х • 3 < 20

Метод подбора.

6 • 3 = 18, 18 < 20

7 • 3 = 21, 21 > 20

х < 7

1 м = 10 дм = 100 см = 1000 мм

1 дм = 10 см = 100 мм

1 см = 10 мм

Задание 856. Спиши, вставляя пропущенные числа.

8 м 6 дм = 86 дм 30 мм = 3 см

6 дм 4 см = 64 см 140 см = 1 м 40 см

Задание 857*. За 1 с звук преодолевает в воздухе расстояние в 330 м. Какое расстояние преодолеет звук за 3 с?

Решение.

330 • 3 = 990 (м) – расстояние преодолеет звук за 3 с.

Ответ: за 3 с. звук преодолеет расстояние 990 м.

Задание 858. Масса масла в кедровых орехах составляет четвёртую часть массы орехов. Сколько масла можно получить из 120 кг этих орехов?

Решение.

120 : 4 = 30 (кг) – масла можно получить.

Ответ: из 120 кг кедровых орехов можно получить 30 кг масла.

Задание 859°. В парке 50 каштанов, клёнов — в 4 раза больше, чем каштанов, а тополей — в 3 раза больше, чем клёнов. Сколько вместе каштанов, клёнов и тополей в парке?

Решение.

50 • 4 = 200 (д.) – клёнов в парке.

200 • 3 = 600 (д.) – тополей в парке.

50 + 200 + 600 = 850 (д.) – всего деревьев в парке.

Ответ: всего деревьев в парке.

Задание 860°

80 • 6 – 250 = 480 – 250 = 230

480 : 6 + 250 = 80 + 250 = 330

40 • 7 + 320 = 280 + 320 = 600

280 : 4 + 481 = 70 + 481 = 551

360 : 4 • 9 = 360 : 36= 10

90 : 6 : 5 = 15 : 5 = 3

Задание 862. (Устно.)

15 • 3 = 45

6 • 12 = 72

72 : 9 = 8

45 : 5 = 9

9 • 4 = 36

1 + 14 = 15

8 : 8 = 1

360 : 6 = 60

60 : 10 = 6

36 • 10 = 360

Задание 863. Объясни способ вычисления:

320 • 3 = (300 + 20) • 3 = 300 • 3 + 20 • 3 = 900 + 60 = 960.

При умножении однозначного числа на трёхзначное можно сначала трёхзначное число разложить на разрядные слагаемые, а потом однозначное число умножить отдельно на слагаемые и результаты прибавить.

Задание 864.

180 • 3 = (100 + 80) • 3 = 100 • 3 + 80 • 3 = 300 + 240 = 540

240 • 2 = (200 + 40) • 2 = 200 • 2 + 40 • 2 = 400 + 80 = 480

150 • 5 = (100 + 50) • 5 = 100 • 5 + 50 • 5 = 500 + 250 = 750

210 • 4 = (200 + 10) • 4 = 200 • 4 + 10 • 4 = 800 + 40 = 840

Задание 865. Суточная порция кухонной соли для одной коровы составляет 65 г. Сколько граммов соли нужно двум коровам на неделю?

Решение.

1 способ. Выражение (65 • 7) • 2

65 • 7 = 455 (г) – соли нужно 1 корове на неделю.

455 • 2 = 910 (г) – соли нужно 2 коровам на неделю.

2 способ. Выражение (65 • 2) • 7

65 • 2 = 130 (г) – соли нужно 2 коровам на один день.

130 • 7 = 910 (г) – соли нужно 2 коровам на неделю.

3 способ. Выражение 65 • 7 • 2 или 65 • 2 • 7

65 • 7 • 2 = 65 • 2 • 7 = 910 (г) – соли нужно 2 коровам на неделю.

Ответ: двум коровам на неделю нужно 910 г кухонной соли.

Задание 866. Составь задачу, подобную предыдущей, зная, что суточная порция соли для коня составляет 32 г.

Суточная порция кухонной соли для одного коня составляет 32 г. Сколько граммов соли нужно двум коням на неделю?

Задание 867. Периметр треугольника DЕК 150 см. Длина стороны ЕК равна 30 см. Сторона DК равна стороне DЕ. Найди длину стороны DЕ. (На рисунке треугольник БЕК уменьшен.)

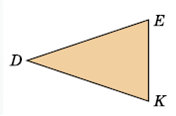
Решение.

150 – 30 = 120 (см) – длина сторон DЕ и DК вместе.

120 : 2 = 60 (см) – длина стороны DЕ.

Ответ: сторона DЕ равна 60 см.

Составь обратную задачу.

Периметр треугольника DЕК 150 см. Длина стороны DЕ равна 60 см. Сторона DК равна стороне DЕ. Найди длину стороны ЕК.

Решение.

60 + 60 = 120 (см) – длина сторон DЕ и DК вместе.

150 – 120 = 30 (см) – длина стороны Ек.

Ответ: длина стороны Ек равна 30 см.

Задание 868*. Три девочки нашли 90 орехов. Они разделили орехи так: старшая взяла на 10 орехов меньше, а младшая — на 10 орехов больше, чем средняя. Сколько орехов взяла каждая девочка?

Решение.

1 способ.

Если 10 орехов младшей сестры отдать старшей, тогда у всех девочек будет поровну орехов.

90 : 3 = 30 (ор.) – орехов в средней девочки.

30 – 10 = 20 (ор.) – орехов у старшей сестры.

30 + 10 = 40 (ор.) – орехов у младшей сестры.

2 способ.

Пускай х (ор.) – орехов у средней сестры, тогда х – 10 (ор.) – орехов у старшей сестры, х + 10 (ор.) – орехов у младшей сестры. Составим уравнение.

х + (х – 10) + (х + 10) = 90

3х = 90

х = 90 : 3

х = 30 (ор.) – орехов у средней сестры.

30 – 10 = 20 (ор.) – орехов у старшей сестры.

30 + 10 = 40 (ор.) – орехов у младшей сестры.

Ответ: у старшей сестры 20 орехов, у средней сестры 30 орехов, у младшей сестры 40 орехов.

Задание 869.

480 • 2 = (400 + 80) • 2 = 400 • 2 + 80 • 2 = 800 + 160 = 960

60 • 10 – 70 • 6 = 600 – 420 = 180

800 : 40 = 20

4 м : 5 = 40 дм : 5 = 8 дм

330 • 3 = 990

100 – 22 • 4 = 100 – 88 = 12

80 : 40 = 2

4 м – 5 дм = 40 дм – 5 дм = 35 дм

Задание 870. Один насос накачивает 640 вёдер воды за 8 мин, а второй — 420 вёдер за 6 мин. Сколько вёдер воды накачают оба насоса за 1 мин?

Решение.

640 : 8 = 80 (в.) – вёдер воды выкачивает один насос за 1 мин.

420 : 6 = 70 (в.) – вёдер воды выкачивает второй насос за 1 мин.

80 + 70 = 150 (в.) – вёдер воды выкачают два насоса вместе.

Ответ: оба насоса за 1 мин выкачают 150 вёдер воды.

Задание 871.

а	800	120	48
b	600	60	30
(а – b) • 4	800	240	72

А	600	80	240
B	200	80	120
(а + b) : 4	200	40	90

Задание 872. Для пошива 5 кепок нужно 15 дм сукна. Сколько таких кепок можно сшить из 12 м сукна?

Решение.

12 м = 120 дм

15 : 5 = 3 (дм) – сукна нужно на 1 кепку.

120 : 3 = 40 (к.) – таких кепок можно сшить.

Ответ: можно сшить 40 таких кепок.

Задание 873. Купили 6 кг яблок по 7 грн и 10 кг картофеля по 2 грн. О чём можно узнать, вычислив выражения?

Решение.

7 • 6 = 42 (грн) – стоимость яблок.

2 • 10 = 20 (грн) – стоимость картофеля.

10 – 6 = 4 (кг) – на столько больше купили картофеля, чем яблок (на столько меньше купили яблок, чем картофеля).

7 – 2 = 5 (грн) – на столько больше цена яблок, чем картофеля (на столько меньше цена картофеля, чем яблок).

7 • 6 + 2 • 10 = 42 + 20 = 62 (грн) – стоимость покупки.

7 • 6 – 2 • 10 = 42 – 20 = 22 (грн) – на столько больше заплатила за яблока, чем за картофель (на столько меньше заплатила за картофель, чем за яблока).

Задание 874.

230 • 4 – 300 = (200 + 30) • 4 – 300 = 800 + 120 – 300 = 620

110 • 5 + 320 = 550 + 320 = 870

240 • 2 : 6 = (200 + 40) • 2 : 6 = (400 + 80) : 6 = 480 : 6 = 80

400 – 40 • 4 = 400 – 160 = 240

210 – 210 : 7 = 210 – 30 = 180

170 • 3 – 200 = (100 + 70) • 3 – 200 = 300 + (210 – 200) = 310

2 м : 5 = 20 дм : 2 = 10 дм

2 м - 5 см = 200 см – 5 см = 195 см

2 м : 1 дм = 20 дм : 1 дм = 20

Составь задачу по выражению 230 • 4.

Длина дрота в катушке 230 м. Сколько дрота в 4 таких катушках?