Другие задания смотри здесь...
![]()
Задание 876*. Из бумаги в клетку вырежи прямоугольник шириной 2 см, чтобы его периметр был равен 20 см.
Решение.
20 : 2 = 10 (см) – половина периметра (сумма длины и ширины прямоугольника).
10 – 2 = 8 (см) – длина прямоугольника.
Следует вырезать прямоугольник длиной 8 см и шириной 2 см.
Задание 877. За период своего роста одно растение кукурузы испаряет 200 л воды. Сколько вёдер воды испаряют 5 таких растений? (Ведро вмещает 10 л воды.)
Решение.
1 cпособ
200 • 5 = 1000 (л) – литров воды испаряют 5 таких растений.
1000 : 10 = 100 (в.) – вёдер воды испаряют 5 таких растений.
2 способ
200 : 10 = 20 (в.) - вёдер воды испаряет за период своего роста одно растение кукурудзы.
20 • 5 = 100 (в.) - вёдер воды испаряют 5 таких растений.
Ответ: 5 таких растений испаряют 100 вёдер воды.
Напомним, что 1 кг = 1000 г, 1 час = 60 мин, 1 мин = 60 сек, 1 м = 10 дм = 100 см, 1 дм = 10 см
Задание 878.
1 кг – 200 г = 1000 г – 200 г = 800 г
1 кг : 2 = 1000 г : 2 = 500 г
2 хв – 20 с = 2 • 60 с - 20 с = 120 с – 20 с = 100 с
2 год – 2 хв = 2 • 60 хв - 2 хв = 120 хв – 2 хв = 118 хв
2 м – 2 дм 2 см = 2 • 100 см - (2 • 10 см + 2 см)= 200 см – 22 см = 178 см
2 м – 2 см = 2 • 100 см - 2 см = 200 см – 2 см = 198 см
Деление суммы на число. Деление вида 39 : 3, 72 : 6
Задание 879. 18 синих и 12 желтых слив отец разделил поровну между тремя сыновьями. Сколько слив получил каждый сын? (Реши задачу двумя способами по данным планам.)
Решение.
1-й способ:
1) Сколько всего было слив?
18 + 12 = 30 (с.) – слив было всего.
2) Сколько слив получил каждый сын?
30 : 3 = 10 (с.) – слив получил каждый сын.
2-й способ:
1) Сколько синих слив получил каждый сын?
18 : 3 = 6 (с.) – синих слив получил каждый сын.
2) Сколько жёлтых слив получил каждый сын?
12 : 3 = 4 (с.) – жёлтых слив получил каждый сын.
3) Сколько всего слив получил каждый сын?
6 + 4 = 10 (с.) – слив получил каждый сын.
Ответ: каждый сын получил по 10 слив.
Задание 880. Раздели сумму на число в соответствии с порядком выполнения действий у выражениях со скобками.
(16 + 8) : 3 = 24 : 3 = 8
(18 + 30) : 8 = 48 : 8 = 6
(18 + 12) : 3 = 30 : 3 = 10
Задание 881. 1) Рассмотри, как можно разделить сумму на число другим способом. (18 + 12) : 3 = 18 : 3 + 12 : 3 = 6 + 4 = 10
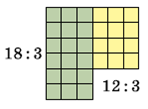
Чтобы разделить сумму на число, можно разделить на это число каждое слагаемое и найденные частные прибавить.
2) Вычисли двумя способами: (24 + 12) : 4.
3) Вычисли удобным способом: (36 + 54) : 6.
Решение.
1) (24 + 12) : 4 = 36 : 4 = 9
(24 + 12) : 4 = (24 : 4) + (12 : 4) = 6 + 3 = 9
2) (36 + 54) : 6 = (36 : 6) + (54 : 6) = 6 + 9 = 15
Задание 882. 20 грузовых и 12 легковых автомобилей разместили на железнодорожных платформах по 4 автомобиля на каждую. Сколько было платформ? (Реши задачу двумя способами.)
Решение.
1 способ. Выражение (20 + 12) : 4
20 + 12 = 32 (ав.) – всего автомобилей.
32 : 4 = 8 (п.) – было платформ.
2 способ. Выражение (20 : 4) + (12 : 4)
20 : 4 = 5 (п.) – было платформ с грузовыми автомобилями..
12 : 4 = 3 (п.) – было платформ с легковыми автомобилями.
5 + 3 = 8 (п.) – было платформ.
Ответ: было 8 платформ.
Задание 883.
(24 + 16) : 8 = 40 : 8 = 5
24 + 16 : 8 = 24 + 2 = 26
170 • 2 – 200 = 340 – 200 = 140
360 : 4 + 90 = 90 + 90 = 180
90 + 6 • 13 = 90 + 78 = 168
200 – 5 • 16 = 200 – 80 = 120
Задание 884*. Построй прямую и обозначь на ней точку О. От точки О отложи на прямой в противоположных направлениях отрезки АО = 45 мм и ОВ = 53 мм. Измерь и вычисли длину отрезка АВ.
Решение.
АВ = АО + ОВ = 45 мм + 53 мм = 98 мм
Задание 885°. 9 одинаковых мешков вмещают 450 кг сахара, а 7 мешков муки — 280 кг. На сколько килограмм масса мешка сахара больше массы мешка муки?
Решение. Выражение (450 : 9) – (280 : 7)
450 : 9 = 50 (кг) – масса мешка сахара.
280 : 7 = 40 (кг) – масса мешка муки.
50 – 40 = 10 (кг) – на столько больше масса мешка сахара, чем муки.
Ответ: масса мешка сахара на 10 кг больше, чем мешка муки.
Задание 886°.
(6 + 15) : 3 = 21 : 3 = 7
(6 + 27) : 3 = 33 : 3 = 11
(8 + 16) : 8 = 24 : 8 = 3
Задание 887. Рассмотри записи и объясни способ деления.
39 : 3 = = (30 + 9) : 3 = = 30 : 3 + 9 : 3 = = 10 + 3 = 13
Задание 888. (Устно.) Найди частные.
84 : 2 = (80 + 4) : 2 = (80 : 2) + (4 : 2) = 42
69 : 3 = (60 + 9) : 3 = (60 : 3) + (9 : 3) = 23
46 : 2 = (40 + 6) : 2 = (40 : 2) + (6 : 2) = 23
Задание 889. Посеяли 4 кг гречихи, а собрали 84 кг. Во сколько раз больше собрали гречихи, чем посеяли?
Решение.
84 : 4 = (80 + 4) : 4 = 21 (раз) – во столько раз больше гречихи собрали, чем посеяли.
Ответ: гречихи собрали в 21 раз больше, чем посеяли.
Задание 890.
|
х • 3 = 96 х = 96 : 3 х = 32 32 • 3 = 96 |
84 : х = 2 х = 84 : 2 х = 42 84 : 42 = 2 |
84 – х = 2 х = 84 – 2 х = 82 84 – 82 = 2 |
Задание 891.
1) 48 – 2 = 46 48 : 2 = 24 48 : 4 = 12 48 : 6 = 8
2) 480 – 2 = 478 480 : 2 = 240 480 : 4 = 120 480 : 6 = 80
Задание 892. Первый кондитер украшает 24 торта за 3 ч, а второй такое же количество тортов украшает за 2 ч. (Задай вопрос и реши задачу). На сколько больше тортов за 1 час украшает второй кондитер, чем первый?
Решение.
24 : 3 = 8 (т.) – тортов украшает первый кондитер за 1 час.
24 : 2 = 12 (т) – тортов украшает второй кондитер за 1 час.
12 – 8 = 4 (т.) – на столько больше за 1 час тортов украшает второй кондитер, чем первый.
Ответ: за 1 час второй кондитер украсит на 4 торта больше, чем первый кондитер.
Задание 893. В пекарне было 90 кг муки. Несколько дней её расходовали по 20 кг в день. Осталось 10 кг. Сколько дней расходовали по 20 кг муки?
Решение.
90 – 10 = 80 (кг) – мука израсходована.
80 : 20 = 4 (дня) – столько дней.
Ответ: расходовали муку 4 дня.
Задание 894*. Как с помощью чашечных весов без гирь отвесить 14 кг сахара, если в пакете его 16 кг?
Решение.
Пересыпать сахар у два мешка ровно и положить на весы (на каждой шальке будет по 16 : 2 = 8 кг). Отложить одну часть. Вторую поделить пополам (на каждой шальке будет 8 : 2 = 4 кг). Отложить одну часть. Другую поделить на две ровные части (на каждой шальке будет 4 : 2 = 2 кг). Отложить одну часть, она будет лишними килограммами.
Сахар будет составлять 14 килограмм.
8 + 4 + 2 = 14 (кг).
Задание 895.
36 : 3 = 12
48 : 2 = 24
24 • 4 = 96
2 • 18 = 36
32 • 2 : 8 = 64 : 8 = 8
21 : 7 + 8 = 3 + 8 = 11
84 : 4 • 3 = 21 • 3 = 63
55 : 5 • 6 = 11 • 6 = 66
Задание 896°. Дуб поглощает 8 вёдер воды ежедневно, осина — 42 ведра в неделю. Сколько вёдер воды поглощают дуб и осина вместе за 5 дней?
Решение.
1 способ. (42 : 7 + 8) • 5
42 : 7 = 6 (в.) – вёдер воды поглощает осина ежедневно.
8 + 6 = 14 (в.) – вёдер воды поглощают вместе ежедневно.
14 • 5 = 70 (в.) – вёдер воды поглощают вместе за 5 дней.
2 способ. 8 • 5 + (42 : 7) • 5
42 : 7 = 6 (в.) – вёдер воды поглощает осина ежедневно.
6 • 5 = 30 (в.) – вёдер воды поглощает осина за 5 дней.
8 • 5 = 40 (в.) – вёдер воды поглощает дуб за 5 дней.
30 + 40 = 70 (в.) – вёдер воды поглощают вместе за 5 дней.
Ответ: за 5 дней дуб и осина поглощают 70 вёдер воды.
Задание 897. Вычисли с комментированием: 64 : 2, 48 : 4, 99 : 3.
64 : 2 = (60 + 4) : 2 = (60 : 2) + (4 : 2) = 30 + 2 = 32
48 : 4 = (40 + 8) : 4 = (40 : 4) + (8 : 4) = 10 + 2 = 12
99 : 3 = (90 + 9) : 3 = (90 : 3) + (9 : 3) = 30 + 3 = 33
Задание 898. Рассмотри записи и объясни способ деления.
72 : 3 = (60 + 12) : 3 = (60 : 3) + (12 : 3) = 20 + 4 = 24
50 : 2 = (40 + 10) : 2 = 20 + 5 = 25
Задание 899. (Устно.) Закончи вычисления.
60 : 5 = (50 + 10) : 5 = 10 + 2 = 12
81 : 3 = (60 + 21) : 3 = 20 + 7 = 27
Задание 900. Разложи делимое на удобные слагаемые и выполни деление:
68 : 4 = (40 + 28) : 4 = (40 : 4) + (28 : 4) = 17
96 : 2 = (80 + 16) : 2 = (80 : 2) + (16 : 2) = 48
51 : 3 = (30 + 21) : 3 = (30 : 3) + (21 : 3) = 17
95 : 5 = (50 + 45) : 5 = (50 : 5) + (45 : 5) = 19