Другие задания смотри здесь...
![]()
Задание 951°. Из 75 л молока получили 3 кг масла. Сколько килограммов масла получат из 100 л молока?
Решение.
1 способ.
75 л молока – 3 кг масла
100 л молока - ? кг масла.
75 : 3 = 25 (л) – молока требуется для 1 кг масла.
100 : 25 = 4 (кг) – масла получат из 100 л молока.
2 способ.
75 л молока – 3000 г масла
100 л молока - ? г масла.
3000 : 75 = 40 (г) – масла получат с 1 л молока.
40 • 100 = 4000 (г) = 4 (кг) – масла получат из 100 л молока.
Ответ: получат 4 кг масла.
Задание 952. Из выражений на умножение и их результатов составь равенства с делением на двузначное число.
|
24 • 3 = 72 72 : 24 = 3 |
34 • 2 = 68 68 : 34 = 2 |
17 • 5 = 85 85 : 17 = 5 |
Задание 954.
|
х • 16 = 80 х = 80 : 16 х = 5 5 • 16 = 80 80 = 80 |
54 : х = 3 х = 54 : 3 х = 18 54 : 18 = 3 3 = 3 |
х : 15 = 3 х = 3 • 15 х = 45 45 : 15 = 3 3 = 3 |
Задание 955. Две портнихи должны сшить по 96 сорочек. Одна шьёт в день 12 сорочек, а вторая — 16. Какая портниха выполнит работу раньше и на сколько дней?
Решение.
96 : 12 = 8 (дн.) – время для пошива в первой портнихи.
96 : 16 = 6 (дн.) – время для пошива во второй портнихи.
8 – 6 = 2 (дн.) – на столько дней первая портниха выполнит работу раньше, чем вторая портниха.
Ответ: первая портниха выполнит работу на 2 дня раньше, чем вторая портниха.
Задание 956. Токарь изготовил 100 деталей. Первые 3 ч он делал по 12 деталей в час, а потом начал изготавливать по 16 деталей в час. Сколько часов токарь изготавливал по 16 деталей?
Решение.
12 • 3 = 36 (д.) – сделал деталей сначала.
100 – 36 = 64 (д.) – деталей изготовил потом.
64 : 16 = 4 (ч.) – часов работал токарь потом.
Ответ: 4 часа токарь изготавливал по 16 деталей.
Задание 957*. За год строители должны возвести 72 выставочные павильона. Первые три квартала они возводили по 18 павильонов. В октябре и ноябре — по 6 павильонов, а в декабре — 8. Выполнено ли годовое обязательство?
Решение.
18 • 3 = 54 (п.) – павильонов возвели за первые три квартала.
6 • 2 = 12 (п.) – павильонов возвели в октябре и ноябре вместе.
12 + 8 = 20 (п.) – павильонов возвели за четвёртый квартал.
54 + 20 = 74 (п.) – павильонов возвели всего за год.
74 – 72 = 2 (п.) – на столько павильонов перевыполнили годовое обязательство.
Ответ: годовое обязательство перевыполнено.
Задание 958.
45 : 5 = 9
32 : 8 = 4
70 : 14 = (28 + 42) : 14 = (28 : 14) + (42 : 14) = 2 + 3 = 5
42 : 21 = (21 + 21) : 21 = (21 : 21) + (21 : 21) = 1 + 1 = 2
2 • 37 = 2 • (30 + 7) = (2 • 30) + (2 • 7) = 60 + 14 = 74
54 : 18 = (18 + 36) : 18 = (18 : 18) + (36 : 18) = 1 + 2 = 3
28 : 4 + 3 • 7 = 7 + 21 = 28
540 : 3 + 180 = (240 + 300) : 3 + 180 = (240 : 3) + (300 : 3) + 180 = 80 + 100 + 180 = 360
Задание 959. Масса шести коробок с печеньем 48 кг. Какова масса восьми коробок с конфетами, если коробка с конфетами на 3 кг тяжелее коробки с печеньем?
Решение.
48 : 6 = 8 (кг) – масса коробки с печеньем.
8 + 3 = 11 (кг) – масса коробки с конфетами.
11 • 8 = 88 (кг) – масса восьми коробок с конфетами.
Ответ: масса восьми коробок с конфетами 88 кг.
Задание 960. Сравни, как изменяется произведение при изменении одного из множителей в несколько раз.
|
а |
3 |
3 |
3 |
3 |
|
b |
2 |
4 |
6 |
8 |
|
а • b |
6 |
12 |
18 |
24 |
|
а |
3 |
6 |
9 |
12 |
|
b |
2 |
2 |
2 |
2 |
|
а • b |
6 |
12 |
18 |
24 |
Если один из множителей увеличить (уменьшить) в несколько раз, то и произведение увеличивается (уменьшается) во столько же раз.
Задание 961.
|
12 • 3 = 36 3 • 17 = 51 13 • 4 = 52 25 • 6 = 150 26 • 3 = 78 |
12 • 18 = 216 15 • 17 = 255 130 • 4 = 520 25 • 18 = 450 260 • 3 = 780 |
Задание 962.
1) В выражении 24 • 6 один из множителей увеличь в 2 раза, а второй уменьши в 2 раза и сравни произведения.
24 • 6 = 20 • 6 + 4 • 6 = 144
48 • 3 = 40 • 3 + 8 • 3 = 144
Произведения равны.
2) Сравни множители и произведения в колонках.
24 • 6 = (20 • 6) + (4 • 6) = 144
72 • 2 = (70 • 2) + (2 • 2) = 144
Произведения равны.
20 • 8 = 160
40 • 4 = 160
Произведения равны.
9 • 15 = (9 • 10) + (9 • 5) =135
27 • 5 = (20 • 5) + (7 • 5) = 135
Произведения равны.
Если один множитель увеличить (уменьшить) в несколько раз, а другой уменьшить (увеличить) в столько же раз, то значение произведения не изменится.
Задание 963. Вычисли по образцу и сделай вывод о способе умножения на 5.
18 • 5 = (18 : 2) • (5 • 2) = 9 • 10 = 90
14 • 5 = (14 : 2) • (5 • 2) = 7 • 10 = 70
24 • 5 = (24 : 2) • (5 • 2) = 12 • 10 = 120
46 • 5 = (46 : 2) • (5 • 2) = 23 • 10 = 230
28 • 5 = (28 : 2) • (5 • 2) = 14 • 10 = 140
Чтобы умножить число на 5, можно сначала его уменьшить в 2 раза, а потом увеличить в 2 раза.
Задание 964. Цветочница составила 8 букетов по 5 роз и 6 букетов по 5 гвоздик. Сколько всего цветков использовала цветочница?
Решение.
1 способ. Выражение (8 • 5) + (5 • 6)
8 • 5 = 40 (цв.) – цветков роз использовала цветочница.
5 • 6 = 30 (цв.) – цветков гвоздик использовала цветочница.
40 + 30 = 70 (цв.) – цветков использовала цветочница.
2 способ. Выражение 5 • (8 + 6)
8 + 6 = 14 (б.) – букетов составила цветочница.
5 • 14 = 70 (цв.) – цветков использовала цветочница.
Ответ: цветочница использовала 70 цветков.
Составь и реши обратную задачу.
Цветочница составила 8 букетов из роз и 6 букетов с гвоздик с одинаковым количеством цветков в каждом букете. Сколько цветков в одном таком букете, если цветочница использовала 70 цветков?
Решение.
8 + 6 = 14 (б.) – букетов составила цветочница.
70 : 14 = 5 (ц.) – цветков в одном таком букете.
Ответ: в одном букете 5 цветков.
Задание 965. В авиационном училище 320 курсантов. 80 курсантов летают с инструктором, в 2 раза меньше курсантов — самостоятельно, а остальные еще учатся на тренажёрах. Сколько курсантов учится на тренажёрах?
Решение. Выражение 320 – (80 + 80 : 2)
80 : 2 = 40 (к.) – курсантов летают самостоятельно.
80 + 40 = 120 (к.) – курсантов летают с инструктором и самостоятельно.
320 – 120 = 200 (к.) – курсантов учатся на тренажёрах.
Ответ: на тренажёрах учится 200 курсантов.
Замени слово «меньше» словом «больше». Изменится ли план решения задачи?
В авиационном училище 320 курсантов. 80 курсантов летают с инструктором, в 2 раза больше курсантов — самостоятельно, а остальные еще учатся на тренажёрах. Сколько курсантов учится на тренажёрах?
Решение. Выражение 320 – (80 + 80 • 2)
80 • 2 = 160 (к.) – курсантов летают самостоятельно.
80 + 160 = 240 (к.) – курсантов летают с инструктором и самостоятельно.
320 – 240 = 80 (к.) – курсантов учатся на тренажёрах.
Ответ: на тренажёрах учится 80 курсантов.
Задание 966*. 12 третьеклассников участвовало в соревнованиях по бегу, 10 - по прыжкам, а 5 — по бегу и прыжкам. Сколько всего третьеклассников было на соревнованиях?
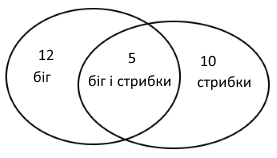
Решение.
1 способ. Выражение 12 + (10 – 5)
10 – 5 = 5 (уч.) – учеников участвовало только по прыжкам.
12 + 5 = 17 (уч.) – учеников было на соревнованиях.
2 способ. Выражение (12 – 5) + 7
12 – 5 = 7 (уч.) – учеников участвовало только по бегу.
7 + 10 = 17 (уч.) – учеников было на соревнованиях.
3 способ. Выражение (12 + 10) - 5
12 + 10 = 22 (уч.) – учеников участвовало по бегу, по прыжкам, по бегу и прыжкам вместе.
22 – 5 = 17 (уч.) – учеников было на соревнованиях.
Ответ: на соревнованиях было 17 учеников.
Задание 967.
46 • 5 = (46 : 2) • 10 = 23 • 10 = 230
32 • 5 = (32 : 2) • 10 = 16 • 10 = 160
94 + 5 = 99
78 + 5 = 83
4 • 24 – 38 : 2 = 96 – 19 = 77
5 • 26 + 48 • 5 = (26 + 48) • 5 = 74 • 5 = 370
36 • 10 = 360
72 • 5 = (72 : 2) • (5 • 2) = 36 • 10 = 360
Задание 968. В парке 240 кустов сирени. В конце апреля расцвело 60 кустов белой сирени, а розовой — в 2 раза больше. Сколько кустов сирени ещё не расцвело?
Решение.
60 • 2 = 120 (к.) – кустов розовой сирени расцвело.
60 + 120 = 180 (к.) – кустов сирени расцвело.
240 – 180 = 60 (к.) – кустов сирени ещё не расцвело.
Ответ: ещё не расцвело 60 кустов сирени.
Задание 969.
360 : 10 = 36
800 : 100 = 8
900 : 10 = 90
480 : 4 = 120
Задание 970. Сравни, как изменяется частное вследствие увеличения (уменьшения) делимого в несколько раз.
|
а |
8 |
16 |
24 |
|
b |
2 |
2 |
2 |
|
а : b |
4 |
8 |
12 |
|
k |
18 |
9 |
3 |
|
t |
3 |
3 |
3 |
|
k : t |
6 |
3 |
1 |
Если делимое увеличить (уменьшить) в несколько раз при неизменном делителе, то частное увеличится (уменьшится) во столько же раз.
Задание 971. Сравни выражения в каждой колонке. Найди значения выражений нижней строки, используя значение соответствующих выражений верхней.
|
36 : 3 = 12 72 : 8 = 9 96 : 16 = 6 75 : 25 = 3 |
360 : 3 = (36 • 10) : 3 = (36 : 3) • 10 = 12 • 10 = 120 720 : 8 = (72 • 10) : 8 = (72 : 8) • 10 = 9 • 10 = 90 960 : 16 = (96 • 10) : 16 = (96 : 16) • 10 = 6 • 10 = 60 750 : 25 = (75 • 10) : 25 = (75 : 25) • 10 = 3 • 10 = 30 |
Задание 972. С одной грядки собрали 15 кг лука, а со второй – в 3 раза больше. Весь лук разложили в сетки по 5 кг. Сколько вышло сеток с луком?
Решение. Выражение (15 + 15 • 3) : 5
15 • 3 = 45 (кг) – лука собрали со второй грядки.
15 + 45 = 60 (кг) – весь лук.
60 : 5 = 12 (с.) – сеток с луком вышло.
Ответ: вышло 12 сеток с луком.
Реши задачу по схеме □ : □ + (□ : □) • □.
Решение. Выражение 15 : 5 + (15 : 5) • 3
15 : 5 = 3 (с.) – сеток с луком собрали с первой грядки.
3 • 3 = 9 (с.) – сеток с луком собрали со второй грядки.
3 + 9 = 12 (с.) – сеток с луком вышло.
Ответ: вышло 12 сеток с луком.
Задание 973. Бабушка развесила на чердаке сушиться 15 пучков травы зверобоя, мяты — на 5 пучков меньше, а крапивы — столько, сколько зверобоя и мяты вместе. Сколько пучков крапивы заготовила бабушка?
Решение. Выражение 15 + (15 – 5)
15 – 5 = 10 (п.) – пучков мяты заготовила бабушка.
15 + 10 = 25 (п.) – пучков зверобоя и мяты вместе заготовила бабушка, или пучков крапивы.
Ответ: бабушка заготовила 25 пучков крапивы.
Задание 974*. Сколько будет десятков, если 2 десятка умножить на 4 десятка?
2 дес. • 4 дес. = 80 дес.
20 • 40 = 800
2 дес. • 4 дес. = 2 • 1 дес. • 4 • 1 дес. = 2 • 10 • 4 дес. = 80 дес.
Задание 975°. Дети собрали и сдали в аптеку 4 кг цветков мать-и-мачехи, 8 кг берёзовых почек, а молодых побегов сосны — в 5 раз больше, чем цветков мать-и-мачехи и берёзовых почек вместе. Сколько килограммов побегов сосны собрали дети?
Решение. Выражение (4 + 8) • 5
4 + 8 = 12 (кг) – цветков мать-и-мачехи и берёзовых почек вместе.
12 • 5 = 60 (кг) – побегов сосны собрали дети.
Ответ: дети собрали 60 кг побегов сосны.