Другие задания смотри здесь...
![]()
Задание 1051. Сколько отдельных квадратов можно сложить из 11 одинаковых палочек? (Проверь решение задачи практически.)
Решение:
11 : 4 = 2 (ост. 3).
Ответ: 2 квадрата.
Задание 1052. Сколько отдельных треугольников можно сложить из 11 одинаковых палочек?
Решение:
11 : 3 = 3 (ост. 2).
Ответ: 3 треугольника.
Задание 1053.
|
7 + 8 < 7 • 8 1 • 9 > 0 • 9 8 : 1 > 6 : 1 |
40 : 4 > 45 : 5 12 – 3 > 12 : 3 15 • 4 = 90 – 30 |
Задание 1054*. Дети взвешивали своих домашних питомцев парами. Мурзик и Тузик вместе весят 19 кг, Мурзик и Бобик вместе весят 27 кг, а Тузик и Бобик — 40 кг. Кто сколько весит?
Решение.
1 способ
19 + 27 + 40 = 86 (кг) весили бы 2 Мурзика, 2 Тузика, 2 Бобика вместе.
86 : 2 = 43 (кг) – весят Мурзик, Тузик, Бобик вместе.
43 – 40 = 3 (кг) – весит Мурзик.
43 – 27 = 16 (кг) – весит Тузик.
43 – 19 = 24 (кг) – весит Бобик.
2 способ
19 + 27 = 46 (кг) – весили бы 2 Мурзика, Тузик, Бобик.
46 – 40 = 6 (кг) – весили бы 2 Мурзика.
6 : 2 = 3 (кг) – весит Мурзик.
19 – 3 = 16 (кг) – весит Тузик.
27 – 3 = 24 (кг) – весит Бобик.
Ответ: Мурзик весит 3 кг, Тузик – 16 кг, Бобик – 24 кг.
Задание 1055.
15 : 5 = 3
16 : 5 = 3 (ост.1)
30 : 6 = 5
32 : 6 = 5 (ост.2)
45 : 9 = 5
48 : 9 = 5 (ост.3)
64 : 8 = 8
67 : 8 = 8 (ост.3)
Задание 1056°. В первом ящике 20 кг помидоров, а во втором — 12 кг. Из второго ящика продали 8 кг помидоров. Во сколько раз стало больше помидоров в первом ящике, чем во втором?
Решение.
12 – 8 = 4 (кг) – помидоров осталось во втором ящике.
20 : 4 = 5 (раз) - во сколько раз стало больше помидоров в первом ящике, чем во втором.
Ответ: стало в 5 больше помидоров в первом ящике, чем во втором.
Задание 1057. Выполни деление с остатком.
Образец рассуждения. Пусть надо разделить 27 на 6. Найдём наибольшее из чисел от 1 до 27, которое делится нацело на 6. Это 24; 24 : 6 = 4. Найдём остаток: 27 - 24 = 3. Следовательно, 27 : 6 = 4 (ост. 3).
27 : 6 = 4 (ост. 3).
48 : 7 = 6 (ост. 6) 54 : 8 = 6 (ост. 6) 20 : 6 = 3 (ост. 2)
Задание 1058. Чашка стоит 8 грн. Сколько таких чашек можно купить на 35 грн?
Решение.
35 : 8 = 4 (ост. 3) - можно купить 4 чашки.
Ответ: можно купить 4 чашки.
Задание 1059. Для посадки привезли 24 саженца яблонь и 8 саженцев груш. 1/4 деревьев посадили дети, а остальные — взрослые. Сколько саженцев посадили взрослые?
Решение.
1 способ
24 + 8 = 32 (с.) – всего саженцев привезли.
32 : 4 = 8 (с.) – саженцев посадили дети.
32 – 8 = 24 (с.) – саженцев посадили взрослые.
2 способ
24 + 8 = 32 (с.) – всего саженцев привезли.
32 : 4 = 8 (с.) – саженцев составляют 1 часть.
4 – 1 = 3 (части) – частей составляют саженцы взрослых.
8 • 3 = 24 (с.) – саженцев посадили взрослые.
Ответ: 24 саженца посадили взрослые.
Задание 1060. Туристы поездом проехали 240 км, автобусом — на 180 км меньше, чем поездом, а пешком прошли 1/5 того пути, который проехали автобусом. Сколько километров туристы прошли пешком?
Решение.
240 – 180 = 60 (км) – расстояние проехали автобусом.
60 : 5 = (50 + 10) : 5 = 12 (км) – расстояние прошли пешком.
Ответ: 12 км туристы прошли пешком.
Задание 1061.
|
х - 48 : 6 = 204 х – 8 = 204 х = 204 + 8 х = 212 212 – 48 : 6 = 212 – 8 = 204 204 = 204 |
23 • 5 – х = 42 115 – х = 42 х = 115 – 42 х = 73 23 • 5 – 73 = 115 – 73 = 42 42 = 42 |
|
х : 6 = 305 – 297 х : 6 = 8 х = 6 • 8 х = 48 48 : 6 = 8 305 – 297 = 8 8 = 8 |
600 : х = 34 + 26 600 : х = 60 х = 600 : 60 х = 10 600 : 10 = 60 34 + 26 = 60 60 = 60 |
|
х • (38 – 29) = 72 х • 9 = 72 х = 72 : 9 х = 8 8 • (38 – 29) = 8 • 9 = 72 72 = 72 |
6 • х = 720 : 8 6 • х = 90 х = 90 : 6 х = 15 6 • 15 = 90 720 : 8 = 90 90 = 90 |
Задание 1062. Составь и запиши три выражения на деление с делителем 8, чтобы при вычислении первого выражения остаток равнялся 0, второго — 3, а третьего — 7.
80 : 8 = 10 83 : 8 = 10 (ост. 3) 87 : 8 = 10 (ост. 7)
Задание 1063*. В гараже стоит 30 автомобилей. У грузовых автомобилей по 6 колёс, а у легковых — по 4. Сколько каких автомобилей в гараже, если всего колёс 168?
Решение.
1 способ
4 • 30 = 120 (к.) – количество колёс всего по 4 шт.
168 – 120 = 48 (к.) – дополнительные по 2 колеса в грузовых автомобилей.
48 : 2 = 24 (ав.) – грузовых автомобилей.
30 – 24 = 6 (ав.) – легковых автомобилей.
2 способ (для старших классов).
Пускай х (ав.) – легковые автомобили, тогда 30 – х (ав.) – грузовые автомобили. 4х (к.) – колёс в легковых автомобилях, 6 • (30 - х) = 180 – 6х (к.) – колёс в грузовых автомобилях. Составим уравнение:
4 • х + 180 – 6 • х = 168
180 + 4 • х – 6 • х = 168
180 + 4 • х – 4 • х – 2 • х = 168
180 – 2 • х = 168
2 • х = 180 – 168
2 • х = 12
х = 12 : 2
х = 6 (ав.) – легковых автомобилей.
30 – х = 30 – 6 = 24 (ав.) – грузовых автомобилей.
Ответ: в гараже 6 легковых автомобилей и 24 грузовых автомобиля.
Задание 1064°. Выполни деление с остатком.
22 : 7 = 3 (ост. 1)
12 : 5 = 2 (ост. 2)
40 : 7 = 5 (ост. 5)
14 : 3 = 4 (ост. 2)
50 : 7 = 7 (ост. 1)
21 : 6 = 3 (ост. 3)
60 : 7 = 8 (ост. 4)
25 : 4 = 6 (ост. 1)
75 : 6 = 12 (ост. 3)
33 : 8 = 4 (ост. 1)
Задание 1065°. У фермера были утки и гуси. Всего 60 птиц. Гуси составляли шестую часть всех птиц. Сколько было уток?
Решение.
1 способ
60 : 6 = 10 (птиц) – гусей у фермера.
60 – 10 = 50 (птиц) – уток у фермера.
2 способ
60 : 6 = 10 (птиц) – птиц составляют 1 часть.
6 – 1 = 5 (часть) – частей составляют утки.
10 • 5 = 50 (птиц) – уток у фермера.
Ответ: 50 уток у фермера.
Задание 1066. Составь истинные равенства по блок-схемам.
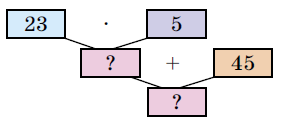
23 • 5 + 45 = (20 + 3) • 5 + 45 = 100 + 15 + 45 = 160
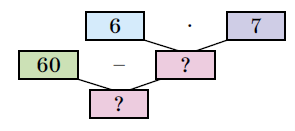
60 – (6 • 7) = 60 – 42 = 18
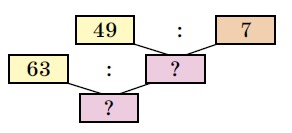
63 : (49 : 7) = 63 : 7 = 9
Задание 1067. Проверь, правильно ли указаны остатки при делении на 2, 3, 4, 5, и сделай вывод.
|
|
11 |
12 |
13 |
14 |
15 |
16 |
17 |
18 |
19 |
20 |
|
2 |
1 |
— |
1 |
— |
1 |
— |
1 |
— |
1 |
— |
|
3 |
2 |
— |
1 |
2 |
— |
1 |
2 |
— |
1 |
2 |
|
4 |
3 |
— |
1 |
2 |
3 |
— |
1 |
2 |
3 |
— |
|
5 |
1 |
2 |
3 |
4 |
— |
1 |
2 |
3 |
4 |
— |
Какими цифрами заканчиваются числа, которые делятся на 2 нацело? А на 5?
На 2 нацело делятся цифры, которые оканчиваются парной цифрой.
На 5 нацело делятся цифры, которые оканчиваются цифрой 0 или 5.
Задание 1068. Какой наибольший остаток может быть при делении на 7; на 9?
При делении остаток всегда меньше делителя.
Решение.
6 – наибольший остаток при делении на 7.
8 – наибольший остаток при делении на 9.
Задание 1069. В хоре 36 детей. Девятая часть всех детей — мальчики, а остальные — девочки. На сколько больше в хоре девочек, чем мальчиков?
Решение.
1 способ
36 : 9 = 4 (д.) – среди детей мальчиков в хоре.
36 – 4 = 32 (д.) – девочек в хоре.
32 – 4 = 28 (детей) – на столько больше девочек, чем мальчиков.
2 способ
36 : 9 = 4 (детей) – детей составляют 1 часть (мальчиков в хоре).
9 – 1 = 8 (частей) – частей составляют девочки.
4 • 8 = 32 (детей) – девочек в хоре.
32 – 4 = 28 (детей) – на столько больше девочек, чем мальчиков.
Ответ: на 28 девочек больше, чем мальчиков.
Задание 1070. Подбери значения переменных, чтобы неравенства были истинными.
|
х • 6 < 86 – 58 х • 6 < 28 х = 1, 2, 3, 4 |
х : 7 > 42 : 7 Частное больше там, где больше делимое х > 42 х = 49, 56, 63 |
64 – х < 34 64 – х < 64 – 30 Разность меньше там, где больше вычитаемое. х > 30 х = 31, 32, 33, … |
Задание 1071. В первый день мастер изготовил 10 деталей, что составляет пятую часть заказа, а во второй 1/4 остальных. Сколько деталей изготовил мастер во второй день?
Решение.
Если 10 деталей уже составляет пятую часть заказа, тогда
10 • 5 = 50 (д.) – деталей всего (деталей заказано).
50 – 10 = 40 (д.) – деталей осталось на второй день.
40 : 4 = 10 (д.) – деталей изготовил во второй день.
Ответ: 10 деталей изготовил во второй день.
Измени вопрос, чтобы в решении добавилось ещё одно действие.
Сколько всего деталей изготовил мастер?
10 + 10 = 20 (д.) – деталей всего изготовил мастер.
Ответ: всего 10 деталей изготовил мастер.
Задание 1072*. Игра. Игроков двое. В горке 10 спичек. За один ход игрок может брать 1 или 3 спички. Выигрывает тот, кто возьмёт одну последнюю спичку. Сколько спичек в начале должен взять первый игрок, чтобы выиграть?
Решение.
10 – 1 = 9 (с.) – спичек должны выбрать два игрока.
1 + 1 + 1 + 1 + 1 + 1 + 1 + 1 + 1
1 + 1 + 1 + 1 + 1 + 1 + 3
1 + 1 + 1 + 3 + 3
3 + 3 + 3
Последнюю спичку всегда будет брать второй игрок. Первый игрок всегда будет в проигрыше.
Задание 1073°. Девочка потратила 3 грн, что составляет пятую часть всех её денег. На сколько больше денег осталось, чем она потратила?
Решение.
Если 3 грн уже составляет 5 часть от всех денег, тогда
3 • 5 = 15 (грн) – денег всего было в девочки.
15 – 3 = 12 (грн.) – денег осталось.
12 – 3 = 9 (грн) – на столько больше денег осталось, чем потратила.
Ответ: на 9 грн больше осталось, чем потратила.
Задание 1074°.
|
х : (450 – 390) = 4 х : 60 = 4 х = 60 • 4 х = 240 240 : (450 – 390) = 240 : 60 = 4 4 = 4 |
56 : х = 800 : 100 56 : х = 8 х = 56 : 8 х = 7 56 : 7 = 8 800 : 100 = 8 8 = 8 |
|
39 – х = 49 : 7 39 – х = 7 х = 39 – 7 х = 32 39 – 32 = 7 49 : 7 = 7 7 = 7 |
(360 : 6) : х = 4 60 : х = 4 х = 60 : 4 х = 15 (360 : 6) : 15 = 60 : 15 = 4 4 = 4 |
Задание 1075.
1/5 от 2 м = 2 м : 5 • 1 = 200 см : 5 • 1 = 40 см
1/10 от 3 ц = 3 ц : 10 • 1 = 300 кг : 10 • 1 = 30 кг
1/6 от 2 суток = 2 суток : 6 • 1 = 2 • 24 ч. : 6 • 1 = 48 ч. : 6 = 8 ч.