Другие задания смотри здесь...
![]()
Задание 1076. Составь равенства по образцу.
36 : 7 = 5 (ост. 1) 38 : 6 = 6 (ост. 2) 53 : 9 = 5 (ост. 8)
36 = 5 • 7 + 1 38 = 6 • 6 + 2 53 = 5 • 9 + 8
Если прибавим остаток к произведению частного и делителя и получим делимое, то деление выполнено правильно.
Задание 1077. Не вычисляя, найди ошибки.
42 : 6 = 6 (ост. 6) неправильно : остаток всегда меньше делителя
54 : 7 = 7 (ост. 5) правильно
55 : 6 = 8 (ост. 7) правильно
74 : 9 = 8 (ост. 2) правильно
Задание 1078. Сторона квадрата а. Запиши равенство для нахождения периметра квадрата.
Решение.
Поскольку, квадрат – прямоугольник с равными сторонами, тогда
Р = а • 4 = 4а
Задание 1079. Периметр участка квадратной формы равен 36 м. Какова длина стороны участка?
Решение.
36 : 4 = 9 (м.) – длина стороны участка.
Ответ: длина стороны участка 9 м.
Задание 1080*. Щенок тяжелее котёнка на 3 кг. Масса двух щенков такая же, как 5 котят. Какова масса щенка?
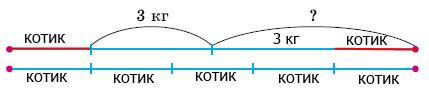
Решение.
Мыслим так: 1 котёнок + 3 кг = 1 щенок, тогда с одной стороны
2 • (1 котёнок + 3 кг) = 2 щенкам.
2 котёнка + 6 кг = 2 щенкам
С другой стороны 5 котят = 2 щенкам.
Сравним обе левые части, имеем
2 котёнка + 6 кг = 5 котятам, тогда 3 котята весят 6 кг
6 : 3 = 2 (кг) – масса котенка.
2 + 3 = 5 (кг) – масса щенка.
Ответ: масса щенка 5 кг.
Задание 1081°. Выполни деление с проверкой.
68 : 9 = 7 (ост. 5) 68 = 7 • 9 + 5
38 : 5 = 7 (ост. 3) 38 = 7 • 5 + 3
64 : 3 = 21 (ост. 1) 64 = 21 • 3 + 1
75 : 2 = 37 (ост. 1) 75 = 37 • 2 + 1
94 : 9 = 10 (ост. 4) 94 = 10 • 9 + 4
Задание 1082°. Масса 6 одинаковых ящиков с печеньем 48 кг. Масса ящика с конфетами на 2 кг больше массы ящика с печеньем. Какова масса 8 ящиков с конфетами?
Решение.
48 : 6 = 8 (кг) – масса ящика с печеньем.
8 + 2 = 10 (кг) – масса ящика с конфетами.
10 • 8 = 80 (кг) – масса 8 ящиков с конфетами.
Ответ: масса 8 ящиков с конфетами 80 кг.
Задание 1083. Произведением каких двух чисел можно заменить число 10?
Каждое число, которое состоит только из десятков и не имеет отдельных единиц, делится на 10, а следовательно, и на 2, и на 5. Поэтому делимость чисел на 2 и на 5 нацело зависит лишь от последней цифры.
На 2 нацело делятся числа, запись которых заканчивается цифрами 0, 2, 4, 6, 8.
На 5 нацело делятся числа, запись которых заканчивается цифрой 5 или 0.
Задание 1084. Не вычисляя, определи, какие числа делятся нацело на 2, а какие на 5: 232, 483, 645, 780, 896, 915.
Решение.
Нацело на 2 делятся числа: 232, 780, 896.
Нацело на 5 делятся числа: 645, 780, 915.
Задание 1085. Первый трактор за 7 ч работы расходует 56 л горючего, а второй — за 1 ч расходует на 2 л меньше. Сколько литров горючего расходует второй трактор за 7 ч? (Реши задачу двумя действиями)
Решение.
2 • 7 = 14 (л.) – на столько меньше горючего за 7 часов израсходует второй трактор.
56 – 14 = 42 (л.) – горючего расходует второй трактор за 7 часов.
Ответ: 42 литра горючего расходует второй трактор за 7 часов.
Задание 1086. Объясни составление неравенств.
|
5 • х = 10 5 • х > 8 5 • х < 11 8 < 5 • х < 11 |
х • 8 = 24 х • 8 < 32 х • 8 > 16 16 < х • 8 < 32 |
х : 2 = 10 х : 2 < 10 х : 2 > 8 8 < х : 2 < 10 |
Для составления неравенств используют знаки > (больше) , < (меньше), = (равно).
Задание 1087*. Двум братьям вместе 20 лет. Один из них в 4 раза старше. Сколько лет каждому?
Решение.
1 способ.
Если один брат у 4 раза больше другого, тогда на первого брата припадает 1 часть, а на второго 4 части от всех лет.
1 + 4 = 5 (частей) – частей составляют 20 лет.
20 : 5 = 4 (года) – лет первому брату (лет составляет одну часть).
4 • 4 = 16 (лет) – лет второму брату.
2 способ (в старшем классе решают)
Пускай х (л.) – лет младшему брату, тогда 4х (л.) – лет старшему брату. Составим уравнение
х + 4х = 20
5х = 20
х = 20 : 5
х = 4 (года) – лет младшему брату.
4х = 4 • 4 = 16 (л.) – лет старшему брату.
Ответ: одному брату 4 года, другому брату 16 лет.
Задание 1088. В столовую привезли 4 мешка белокочанной капусты по 10 кг и 3 мешка цветной капусты. Сколько килограммов цветной капусты в каждом мешке, если всего привезли 64 кг капусты?
Решение.
10 • 4 = 40 (кг) – белокочанной капусты привезли.
64 – 40 = 24 (кг) – цветной капусты привезли.
24 : 3 = 8 (кг) – цветной капусты в 1 мешке.
Ответ: в 1 мешке 8 кг цветной капусты.
Какая из блок-схем отвечает решению задачи?
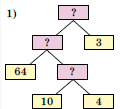
Первая.
Составь обратную задачу по другой блок-схеме.
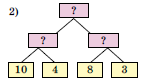
В столовую привезли 4 мешка белокочанной капусты по 10 кг и 3 мешка цветной капусты по 8 кг. Сколько всего привезли капусты?
Решение.
10 • 4 = 40 (кг) – белокочанной капусты привезли.
8 • 3 = 24 (кг) – цветной капусты привезли.
40 + 24 = 64 (кг) – капусты всего привезли.
Ответ: всего привезли 64 кг капусты.
Задание 1089. Подбери значения переменной, чтобы неравенства были истинными.
90 < 13 • х < 100; 80 < 12 • а < 90.
Решение
90 < 13 • 7 < 100, поскольку 13 • 7 = 91
80 < 12 • 7 < 90, поскольку 12 • 7 = 84
Задание 1090.
59 : 9 = 6 (ост. 5)
76 : 10 = 7 (ост. 6)
811 : 10 = 81 (ост. 1)
87 : 30 = 2 (ост. 27)
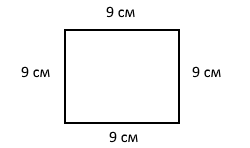
Задание 1091. Построй квадрат, периметр которого равен периметру равностороннего треугольника со стороной 12 см.
Решение.
12 • 3 = 36 (см) – периметр равностороннего треугольника.
36 : 4 = 9 (см) – длина стороны квадрата.
Следует построить квадрат со стороной 9 см.
Задание 1092. Экскурсия началась в 11 ч и длилась 3 ч. В котором часу закончилась экскурсия?
Решение.
11 + 3 = 14 (часов) – время окончания экскурсии.
Ответ: в 14 часов закончилась экскурсия.
Задание 1093°. Магазин начинает работу в 7 ч, а заканчивает в 19 ч. Сколько часов работает магазин, если обеденный перерыв длится 1 ч?
Решение.
19 – 7 = 12 (часов) – время работы от начала до конца.
12 – 1 = 11 (ч.) – часов работает магазин.
Ответ: магазин работает 11 часов.
Задание 1094°.
1/3 от 6 грн = 6 грн : 3 = 2 грн
1/4 от 2 дм = 2 дм : 4 = 20 см : 4 = 5 см
1/5 от 1 ц 5 кг = 1 ц 5 кг : 5 = (100 кг + 5 кг) : 5 = 20 кг + 1 кг = 21 кг
1/2 от 2 м 8 дм =2 м 8 дм : 2 = (2 м + 8 дм) : 2 = 1 м + 4 дм = 1 м 4 дм
1/3 от 1 см 8 мм = 1 см 8 мм : 3 = 18 мм : 3 = 6 мм
Дополнительные упражнения
Задание 1. Вычисли удобным способом.
48 : (4 • 2) = 48 : 8 = 6
560 : (8 : 2) = (560 : 8) : 2 = 70 : 2 = 35
Задание 2.
23 • 2 + 1 = 46 + 1 = 47
64 : 4 – 4 = 16 – 4 = 12
48 : 6 + 2 = 8 + 2 = 10
80 : 5 + 0 = 16
48 : (6 + 2) = 48 : 8 = 6
0 : 7 + 70 = 0 + 70 = 70
24 • 4 – 3 = 96 – 3 = 93
51 : 3 + 7 = 17 + 7 = 24
Задание 3.
2 м : 5 = 20 дм : 5 = 4 дм
2 дм : 5 = 20 см : 5 = 4 см
2 м – 5 дм = 20 дм – 5 дм = 15 дм
2 дм – 5 см = 20 см – 5 см = 15 см
1 кг : 2 = 1000 г : 2 = 500 г
1 кг : 5 = 1000 г : 5 = 200 г
1 кг – 200 г = 1000 г – 200 г = 800 г
1 кг – 2 г = 1000 г – 2 г = 998 г
Задание 4. В детский сад привезли яблоки. На протяжении пяти дней тратили по 9 кг яблок ежедневно. Осталось на 8 кг больше, чем потратили. Сколько килограммов яблок привезли в детский сад?
Решение.
9 • 5 = 45 (кг) – яблок потратили за 5 дней.
45 + 8 = 53 (кг) – яблок осталось.
53 + 45 = 98 (кг) – яблок привезли в детский сад.
Ответ: в детский сад привезли 98 кг яблок.
Задание 5. 36 л сока разлили в банки по 3 л, а 28 л компота — в банки по 2 л. Сколько всего вышло банок?
Решение.
36 : 3 = 12 (б.) – банок вышло для сока.
28 : 2 = 14 (б.) – банок вышло для компота.
12 + 14 = 26 (б.) – банок всего вышло.
Ответ: всего вышло 26 банок.
Составь обратные задачи.
1) Разлили 36 л сока в банки по 3 л, а 28 л компота в банки по 2 л. Сколько вышло банок с компотом, а сколько из соком?
2) Сока и компота вместе Было 64 л. Разлили 36 л сока в банки по 3 л, а компот в банки по 2 л. Сколько вышло банок с компотом?
3) Сока и компота вместе было 64 л. Разлили 28 л компота в банки по 2 л, а сока в банки по 2 л. Сколько вышло банок сока?
4) Сока и компота вместе было 64 л. Разлили 36 л сока в банки по 3 л, а 28 л компота в меньшие банки. Сколько литров в одной банке для компота?
5) Сока и компота вместе было 64 л. Разлили 28 л компота в банки по 2 л, а 36 л сока в большие банки. Сколько литров в одной банке для сока?
Задание 6. Составь и реши задачи по кратким записям.
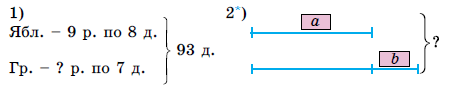
1) В саду 93 дерева. Яблони посадили в 9 рядов по 8 деревьев. Сколько посадили рядов груш по 7 деревьев?
Решение.
8 • 9 = 72 (деревьев) – яблонь посадили.
93 – 72 = 21 (деревьев) – груш посадили.
21 : 7 = 3 (р.) – рядов груш посадили.
Ответ: 3 ряда груш посадили.
2) Длина одной ленты а см, а второй – на b см больше. Какова длина двух лент вместе?
Решение.
а + b (см) – длина второй ленты.
а + (а + b) = 2а + b (см) – длина двух лент вместе.
Ответ: длина двух лент вместе 2а + b сантиметров.
Задание 7. Если ленту разрезать на 4 части по 16 м, то останется ещё 6 м. Но эту ленту разрезали на части по 5 м. На сколько частей её разрезали?
Решение.
16 • 4 + 6 = 64 + 6 = 70 (м) – длина ленты.
70 : 5 = (50 + 20) : 5 = 14 (ч.) – частей ленты.
Ответ: на 14 частей разрезали ленту.
Задание 8. Бригада рабочих по норме должна собирать 48 пылесосов за 4 дня, а собирает их за 3 дня. Сколько пылесосов сверх нормы собирает за день бригада рабочих?
Решение.
48 : 4 = 12 (п.) – пылесосов по норме за 1 день.
48 : 3 = (30 + 18) : 3 = 16 (п.) – пылесосов собирает за 1 день бригада.
16 – 12 = 4 (п.) – пылесоса сверх нормы собирает за день бригада.
Ответ: 4 пылесоса сверх нормы собирает за день бригада.
Задание 9. Один мальчик сказал, что у него братьев и сестёр поровну, а у его сестер братьев вдвое больше, чем сестёр. Сколько детей в этой семье?
Решение.
Метод добора.
Пускай сестра имеет 1 сестру, тогда братьев вдвое больше – два, один из которых мальчик задания, тогда у него один брат и две сестры, что противоречит первому условию, что братьев и сестер поровну.
Пускай сестра имеет 2 сестры, тогда братьев у неё вдвое больше – четыре, один из которых мальчик задания, тогда у него три сестры и три брата, их поровну.
3 + 4 = 7 (д.) – всего детей.
Ответ: в этой семье 7 детей.