Завдання 820 Круг
1) належать колу, що обмежує круг точки B, G, E
2) належать кругу точки B, G, E, A, F, O, N, C
3) не належать кругу точки H, M, D
Завдання 821
Накресли круг із центром у точці О, радіус якого 25 мм. Познач точку A, що належить кругу і не лежить на колі, яке обмежує круг, і точку B, яка не належить кругу. Виміряй відстані OA і ОВ та порівняй їх з радіусом. Чи перетинає відрізок АВ коло?
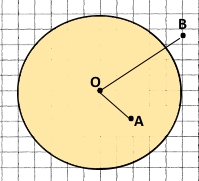
ОА < r, де r — радіус кола.
OB > r, де r — радіус кола.
Відрізок АВ перетинає коло.
Завдання 822, 823 Площа круга заданого радіуса
|
1) S = 3,14 • 4² = 3,14 • 16 = 40,24 (см²)
2) S = 3,14 • 2,5² = 3,14 • 6,25 = 19,625 (дм²)
|
|
1) S = 3,14 • 10² = 3,14 • 100 = 314 (м²)
2) S = 3,14 • 1,2² = 3,14 • 1,44 = 4,5216 (дм²)
|
Завдання 824, 825 Площа круга заданого діаметра
|
1) 2 : 2 = 1 (дм) – радіус круга; S = 3,14 • 1² = 3,14 (дм²)
2) 3,6 : 2 = 1,8 (см) – радіус круга; S = 3,14 • 1,8² = 3,14 • 3,24 = 10,1736 (см²)
|
|
1) 40 : 2 = 20 (см) – радіус круга; S = 3,14 • 20² = 3,14 • 400 = 12,56 (дм²)
2) 1,6 : 2 = 0,8 (см) – радіус круга; S = 3,14 • 0,8² = 3,14 • 0,64 = 2,0096 (дм²)
|
Завдання 826
Зроби потрібні вимірювання та знайди площу круга на малюнку 24.
r = 15 мм; S = 3,14 • 15² = 3,14 • 225 = 706,5 (см²)
Завдання 827
Виміряй кути АОВ і ВОС (мал. 24) і обчисли міру кута АОС. Перевір обчислення за допомогою транспортира.
∠АОВ = 135°, ∠BOC = 90°, тому ∠АОВ = 360° - (135°+ 90°) = 360° - 225° = 135°
Завдання 828
Поділи круг на чотири сектори так, щоб кути трьох з них дорівнювали 70°, 80° і 100°. Зафарбуй ці три сектори в різні кольори. Знайди градусну міру кута незафарбованого сектора. Перевір обчислення за допомогою транспортира.
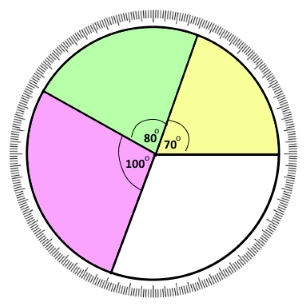
360° – (70°+ 80° + 100°) = 110° – градусна міра незафарбованого сектора.
Завдання 829 Кут сектора
|
1) 360° • 1/3 = 120°
4) 360° • 0,05 = 18°
|
2) 360° • 2/5 = 144°
5) 360° • 0,1 = 36°
|
3) 360° • 7/12 = 210°
6) 360° • 0,5 = 180°
|
Завдання 830
|
1) 360° • 1/5 = 72°
4) 360° • 0,08 = 28,8°
|
2) 360° • 4/9 = 160°
5) 360° • 0,25 = 90°
|
3) 360° • 11/18 = 220°
6) 360° • 0,8 = 288°
|
Завдання 831
Під час реставрації двоповерхової круглої башти всю підлогу покрили кахлями. Скільки квадратних метрів кахлів було використано, якщо внутрішній діаметр башти 6 м?
Розв'язання
1) r = d : 2 = 6 : 2 = 3 (м) – радіус підлоги башти;
2) S = πr² = 3,14 • 3² = 28,26 (см²) – площа підлоги башти;
3) 28,26 • 2 = 56,52 (см²) – площа підлоги двоповерхової башти.
Відповідь: 56,52 см².
Завдання 832
Довжина кола 47,1 м. Знайди площу круга, обмеженого цим колом.
Розв'язання
1) d = C : π = 47,1 : 3,14 = 15 (м) – діаметр круга;
2) r = d : 2 = 15 : 2 = 7,5 (м) – радіус круга;
3) S = πr² = 3,14 • 7,5² = 176,625 (м²) – площа круга.
Відповідь: 176,625 см².
Завдання 833
Довжина кола 50,24 см. Знайди площу круга, обмеженого цим колом.
Розв'язання
1) d = C : π = 50,24 : 3,14 = 16 (cм) – діаметр круга;
2) r = d : 2 = 16 : 2 = 8 (cм) – радіус круга;
3) S = πr² = 3,14 • 8² = 200,96 (cм²) – площа круга.
Відповідь: 200,96 см².
Завдання 834
Радіус одного кола, зображеного на малюнку 25, дорівнює 6 см, а другого — 4 см. Обчисли площу кільця , утвореного цими колами.
Розв'язання
1) S1 = πr² = 3,14 • 6² = 113,04 (м²) – площа більшого круга;
2) S2 = πr² = 3,14 • 4² = 50,24 (м²) – площа меншого круга;
3) S = S2 - S1 = 113,04 - 50,24 = 62,8 (м²) – площа кільця.
Відповідь: 62,8 м².
Завдання 835
Ретрансляційна вишк а спирається на майданчик у формі кільця. Діаметр зовнішнього кола 25 м, а внутрішнього кола — 15 м. Обчисли площу фундаменту вишки.
Розв'язання
1) 25 : 2 = 12,5 (м) – радіус завнішнього круга;
2) 15 : 2 = 7,5 (м) – радіус внутрішнього круга;
1) S1 = πr² = 3,14 • 12,5² = 490,625 (м²) – площа більшого круга;
2) S2 = πr² = 3,14 • 7,5² = 176,625 (м²) – площа меншого круга;
3) S = S2 - S1 = 176,625 - 490,625 = 314 (м²) – площа фундаменту вишки.
Відповідь: 314 м².
Завдання 836
Щоб засіяти 1 м² землі, потрібно 40 г насіння газонної трави. Кілограм такого насіння коштує 120 грн. Скільки коштів знадобиться, щоб засіяти газонною травою ділянку круглої форми радіусом 20 м?
Розв'язання
1) S = πr² = 3,14 • 20² = 3,14 • 400 =1256 (м²) – площа газону;
2) 40 • 1256 = 50240 (г) = 50,240 (кг) – потрібно насіння;
3) 50,240 • 120 = 6028,8 (грн) – знадобиться коштів.
Відповідь: 6028,8 грн.
Завдання 837
Знайди площу 5/7 круга, радіус якого 0,7 м. Відповідь округли до десятих м² .
Розв'язання
1) 3,14 • 0,7² = 1,5386 (м²) – площа круга;
2) 1,5386 • 5/7 = 1,009 (см²) ≈ 1,0 (см²) – площа 5/7 круга.
Відповідь: 1,0 м².
Завдання 838
Знайди площу 2/9 круга, радіус якого 4,5 дм. Відповідь округли до одиниць дм².
Розв'язання
1) 3,14 • 4,5² = 63,585 (дм²) – площа круга;
2) 63,585 • 2/9 = 14,13 (дм²) ≈ 14 (дм²) – площа 2/9 круга.
Відповідь: 14 дм².
Завдання 839
Знайди радіус круга, площа якого дорівнює 314 см².
r² = S/π = 314 : 3,14 = 100 (см), тому радіус круга r = 10
Завдання 840
Знайди радіус круга, площа якого дорівнює 50,24 дм².
r² = S/π = 50,24 : 3,14 = 16 (см), тому радіус круга r = 4
Завдання 841
На кожній стороні квадрата побудовано півкруг (мал. 26). Зроби потрібні вимірювання й обчисли площу утвореної фігури.
Розв'язання
Площа фігури складається з площ квадрата зі стороною 2 см і двох кругів діаметром 2 см.
1) 2 • 2 = 4 (см²) – площа квадрата;
2) 2 : 2 = 1 (см) – радіус круга;
3) 3,14 • 1² • 2 = 6,28 (см²) – площа двох кругів;
4) 4 + 6,28 = 10,28 (см²)
Відповідь: площа фігури 10,28 см².
Завдання 842
|
площа першої зафарбованої фігури
|
площа другої зафарбованої фігури
|
|
1) 3 • 4 = 12 (см²) – площа прямокутника;
2) 3,14 • 1² = 3,14 (см²) – площа круга.
3) 12 – 3,14 = 8,86 (см²)
Відповідь: площа фігури 8,86 см².
|
1) 3 • 3 = 9 (см²) – площа квадрата;
2) 3 : 2 = 1,5 (см) – радіус круга;
3) 3,14 • 1,5² = 7,065 (см²) – площа круга.
4) 9 – 7,065 = 1,935 (см²)
Відповідь: площа фігури 1,935 см².
|
Завдання 843
Розв'язання
1) 4 • 4 = 16 (см²) – площа квадрата;
2) 4 : 2 = 2 (см) – радіус круга;
3) 3,14 • 2² = 12,56 (см²) – площа круга;
4) 16 – 12,56 = 3,44 (см²) – площа фігури.
Відповідь: 3,44 см².
Завдання 844
Радіус першого круга 12 дм, а другого — 4 дм.
Розв'язання
1) 12 : 4 = 3 (р.) – у стільки разів радіус першого круга більший за радіус другого;
2) π • 12² : π • 4² = 144 : 16 = 9 (р.) – у стільки разів площа першого круга більша за площу другого круга.
Відповідь: у 3 рази; у 9 разів.
Зроби висновки. Якщо відношення радіусів двох кіл дорівнює а разів, тоді відношення їхніх площ дорівнює а² разів.
Завдання 845
Круг, радіус якого 3 м, поділено на два сектори (мал. 30). ∠АОВ = 120°. Скільки витратили фарби кожного кольору, якщо на один квадратний метр площі потрібно 0,2 кг фарби? Відповідь округли до десятих кг.
Розв'язання
1) 120°/360° = 1/3 (ч.) – сектора припадає на червоний колір;
2) 1 – 1/3 = 2/3 (ч.) – сектора припадає на зелений колір;
3) 1/3 • 3,14 • 3² = 1/3 • 28,26 = 9,42 (м²) – площа червоного сектора;
4) 0,2 • 9,42 = 1,884 (кг) – витратили фарби червоного кольору;
Площа зеленого сектора удвічі більша, тому й фарби потрібно удвічі більше.
5) 1,884 • 2 = 3,768 (м²) – витратили фарби зеленого кольору.
Відповідь: 1,884 кг і 3,768 кг.
Завдання 846
Автомобіль проїхав 28% відстані між містами. Скільки кілометрів потрібно ще проїхати автомобілю, щоб дістатися пункта призначення, якщо відстань між містами 450 км?
Розв'язання
1) 100% – 28% = 78% – залишилося проїхати;
2) 450 • 0,78 = 351 (км)
Відповідь: потрібно ще проїхати 351 км.
Завдання 847
За першу годину автомобіль проїхав 70 км, після чого йому залишилося проїхати ще 80 % від усієї відстані. Скільки всього кілометрів мав проїхати автомобіль?
Розв'язання
1) 100% – 80% = 20% – проїхав;
2) 70 : 0,2 = 350 (км)
Відповідь: автомобіль мав проїхати 350 км.
Завдання 848
Товар коштував 100 грн. Спочатку його ціну підвищили на 20 %, а потім двічі знижували, причому щоразу на 10 % . Скільки став коштувати товар?
Розв'язання
1) 100 + 100 • 0,2 = 120 (грн) – ціна після першого підвищення;
2) 120 – 120 • 0,1 = 108 (грн) – ціна після другого зниження;
3) 108 – 108 • 0,1 = 97,2 (грн) – став коштувати товар.
Відповідь: 97,2 грн.
Завдання 849
1 м3 неочищених стічних вод забруднює в середньому 50 м3 чистої води. Скільки води щодоби оберігатиметься від забруднення, якщо протягом цього часу споруди очищатимуть 1,4 тис. м3 води? Примітка. 1 м3 = 1000 л.
Розв'язання
1,4 тис. м3 = 1400 м3
1400 • 50 = 70 000 (м3) – щодоби оберігатиметься від забруднення.
Відповідь: 70 000 м3.
Завдання 850
Чи можна трикутник розрізати так, щоб отримати три чотирикутники? Можна.