|
1) 5 > 0; Так
4) –18 > 0; Ні
|
2) –4 < 0; Так
5) 7 > –2; Так
|
3) –9 > 1; Ні
6) 2 < –З. Так
|
Завдання 978, 979
|
Ліворуч
|
Праворуч
|
|
1) В(0) чи А(–5)
2) М(0) чи N(2,9)
3) С(2) чи Р(–3)
|
1) М(0) чи Р(-8)
2) А(7) чи В(0)
3) Т(–5) чи В(0)
|
Завдання 980, 981 Порівняння чисел
|
1) 19 > –28
2) 0 > –131
3) 112 > 0
4) –1,2 < 1,1
|
1) –15 < 13
2) –7 < 0
3) 12 > 0
4) 15 > –3
|
Завдання 982, 983 Записи у вигляді нерівності
|
1) –2 < 0
2) 7,8 > 0
3) х < 0
4) у > 0
5) а < 7
6) b ≤ –2
|
1) 4,5 > 0
2) –3,8 < 0
3) Ь > –2
4) с ≥ 9,5
|
Завдання 984, 985 Порівняння чисел
|
1) –52 > –58
2) –8,4 < –8,3
3) –4,18 > –4,81
4) –3 2/5 < –З 1/5
5) –5,01 < –5,001
6) –6,1 = –6 1/10
7) –3/8 < –1/6
8) –9/16 > –7/12
9) –5/14 > –8/21
|
1) –63 > –64
2) –5,4 < –5,7
3) –7,16 > –7,61
4) –4,02 < –4,002
5) –2/7 > –5/14, бо –2/7 = –4/14
6) –9/20 < –7/16, бо –9/20 = –36/80 і –7/16 = –35/80
|
Завдання 986
У порядку зростання: –4; –3,5; –2; 0; 1; 2,5; 5
Завдання 987
У порядку спадання: 5,5; 4; 2; 0; –3; –4,5; –5
Завдання 988
У порядку спадання числа: 4,7 (І), 3,8 (В), 0,6 (А), –0,3 (С), –3,8 (Ю), –5,2 (К)
ІВАСЮК — прізвище українського композитора-виконавця, Героя України.
Завдання 989
У порядку зростання: –8,7 (X), –7,6 (А), –0,2 (Р), 0,3 (К), 7,8 (І), 8,1 (В)
ХАРКІВ — назва міста-героя України.
Завдання 990
1) Між –5,2 і 2 всі цілі числа: –5; –4; –3; –2; –1; 0; 1
2) Між –8,1 і –3,2 всі цілі числа: –8; –7; –6; –5; –4
Завдання 991
1) Між –2,8 і 4,2 всі цілі числа: –2; –1; 0; 1; 2; 3; 4
2) Між –10,5 і –5,1 всі цілі числа: -10; –9; –8; –7; –6
Завдання 992, 993
Між якими двома сусідніми цілими числами міститься число:
|
1) –7 < –6,1 < –6
2) 4 < 4,3 < 5
3) –4 < –3 1/9 < –2
4) –1 < –0,3 < 0
5) 0 < 0,98 < 1
|
1) –6 < –5,3 < -5
2) –3 < –2 1/18 < –2
3) 6 < 6,2 < 7
4) –1 < –0,29 < 0
5) 0 < 1/9 < 1
|
Завдання 994
1) Порівняй температуру в Києві та Львові в один і той самий час:
|
Дата
|
01.12
|
06.12
|
11.12
|
16.12
|
21.12
|
26.12
|
|
Київ
|
4,7
|
1,2 | –3,2 | –14,7 | –8,9 | –2,7 |
|
Львів
|
3,8 | 0 | –2,1 | –13,9 | –10,1 | 1,3 |
2) У Києві була найвища температура 01.12, а у Львові найнижча 16.12
Завдання 995, 996 Запиши
|
1) –2; –1; 0; 1
2) –4; –3; –2; –1
|
1) –2; –1; 0
2) –5; –4; –3
|
Завдання 997
Познач на координатній прямій усі від'ємні цілі числа, більші за –5,93.
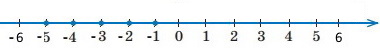
Завдання 998
Познач на координатній прямій усі від'ємні цілі числа, більші за –4,41.
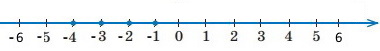
Завдання 999
1) –2,83 < х < 3,1, якщо цілі числа х = –2; –1; 0; 1; 2; 3
2) –0,9 < х < 1,02, якщо цілі числа х = 0 ; 1
3) –6 < х < –2, якщо цілі числа х = –5; –4; –3
Завдання 1000
1) –2,9 < у < 5,4, якщо цілі числа х = –2; –1; 0; 1; 2; 3; 4; 5
2) –3 ≤ у < 4,02, якщо цілі числа х = –3; –2; –1; 0; 1; 2; 3; 4
Завдання 1001
Цілих чисел, які менші від 15,6, але більші за –16,7: 15 + 1 + 16 = 32
Завдання 1002
|
Числа a i b — від'ємні
|
|
|
1) |а| > |b|, тоді a < b
|
2) а > b, тоді |а| < |b|
|
Завдання 1003
1) а ≤ –13,82, при найбільшому цілому числі –14
2) а ≤ –11, при найбільшому цілому числі –11
Завдання 1004
1) m ≥ –19, при найменшому цілому числі –19
2) m ≥ –13,7, при найменшому цілому числі –13
Завдання 1005
1) задовольняє нерівність х ≤ –4 найбільше ціле число –4
2) задовольняє нерівність х ≥ –19 1/2 найменше ціле число –19
Завдання 1006
|
1) d > b
|
2) с > d
|
3) d < 0
|
4) –b > d
|
5) –а < 0
|
6) –b > -с
|
Завдання 1007
Відомо, що а і b — додатні числа, х і у — від'ємні числа. Порівняй:
|
1) 0 > х
5) а > у
|
2) а > 0
6) х < b
|
3) –b < 0
7) –а < b
|
4) 0 < –у
8) –х > у
|
Завдання 1008
Відомо, що m — додатне число, а n — від'ємне. Порівняй:
|
1) 0 < m
4) –m < m
|
2) n < 0
5) n < –n
|
3) m > n
6) –m < –n
|
Завдання 1009
На координатній прямій числа х і у — протилежні, тому а є від'ємним числом.
Завдання 1010
Замість зірочки підстав цифру так, щоб утворилася правильна нерівність (розглянь усі можливі випадки):
1) –4,03 < –4,*1, якщо * = 0
2) –0,3*7 > –0,316, якщо * = 0
3) –7,3*9 < –7,379, якщо * = 8; 9
4) –42,1* < –42,16, якщо * = 7; 8; 9
5) –4,4*4 > –4,442, якщо * = 3; 2; 1; 0
6) –3*,05 < –32,1, якщо * = 3; 4; 5; 6; 7; 8; 9
Завдання 1011
Запиши всі цілі значення змінної х, які одночасно задовольняють нерівності:
1) –5 ≤ х < 6 і –7 < х ≤ 2, якщо всі цілі числа х = –5; –4; –3; –2; –1; 0; 1; 2
–5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5
–6; –5; –4; –3; –2; –1; 0; 1; 2
2) –8,3 < х < –1,2 і |х|≤ 3, якщо всі цілі числа х = –3; –2
–8; –7; –6; –5; –4; –3; –2
–3; –2; –1; 0; 1; 2; 3
Завдання 1012
Запиши всі цілі значення змінної у, які одночасно задовольняють нерівності:
–8,9 < у < 0,2 і –5 ≤ у ≤ 3 , якщо всі цілі числа у = –5; –4; –3; –2; –1; 0
–8; –7; –6; –5; –4; –3; –2; –1; 0
–5; –4; –3; –2; –1; 0; 1; 2; 3
–5; –4; –3; –2; –1; 0
Завдання 1013
–4/5 = –20/25 i –3/5 = –15/25, тому нерівність –4/5 < х < –3/5 задовільняють три дроби:
–19/25; –18/25; –17/25
Завдання 1014
Порівняй х і –х.
Розв'язання
Якщо х > 0, то х > –х; якщо х = 0, то х = –х; якщо х < 0, то х < –х.
Завдання 1015
1) якщо х > 2, то х — додатне число; Так
2) якщо х > –1 , то х — додатне число; Ні (невід'ємне)
3) якщо у < –1 , то у — від'ємне число; Так
4) якщо у < 2, то у — від'ємне число. Ні (недодатне)
Завдання 1016
1) сумі чисел 2,4 і 8 3/5
2,4 + 8,6 = 11, тому протилежне число –11
2) різниці чисел 4 і 1 4/7.
4 – 1 4/7 = 3 7/7 – 1 4/7 = 2 3/7, тому протилежне число –2 3/7
Завдання 1017
У двокімнатній квартирі одна кімната має форму квадрата зі стороною 3,5 м, інша має довжину 5,2 м, а ширину — 3,5 м. Скільки потрібно м2 ламінату, щоб застелити в кімнатах підлогу?
Розв'язання
1) 3,5 • 3,5 = 12,25 (м²) – площа квадратної кімнати;
2) 5,2 • 3,5 = 18,2 (м²) – площа прямокутної кімнати;
3) 12,25 + 18,2 = 30,45 (м²) – потрібно ламінату.
Відповідь: 30,45 м².
Завдання 1018
Сім'я має річний бюджет 140 000 грн. Щомісяця вона витрачає 9000 грн. Чи має змогу ця сім'я раз на рік придбати товари: 1) предмет домашньої техніки ціною 15 000 грн; 2) сімейну оздоровчу путівку вартістю 35 000 грн?
Розв'язання
1) 9000 • 12 = 108 000 (грн) – витрачає за рік;
2) 140 000 – 108 000 = 32 000 (грн) – залишок грошей.
15 000 < 32 000 < 35 000
Відповідь: сім’я раз на рік зможе придбати домашню техніку, але не зможе придбати сімейну оздоровчу путівку.
Завдання 1019
Задача-дослідження. Знайди всі двоцифрові натуральні числа, які кратні добутку своїх цифр.
Нехай двоцифрове число складене з двох цифр a і b, причому a ≠ 0 і b ≠ 0, тоді його можна представити у вигляді: ab = 10a + b,
За умовою (10а + b)/(а • b) = k, звідси
kab = 10a + b, де поділимо вираз на b, одержимо:
ka = 10a/b + 1.
Оскільки числа ka і 1 – цілі, значить, дріб повинен бути цілим числом. Знаменник b має дорівнювати 1 або скоротитися.
Якщо b = 1, тоді маємо ka = 10a/1 + 1, ka = 10a + 1, a(k – 10) = 1, a = 1/(k – 10), при
к = 11, а = 1, маємо число 11
Якщо b = 2, тоді маємо ka = 10a/2 + 1, ka = 5a + 1, a(k – 5) = 1, a = 1/(k – 5), при
к = 6, а = 1, маємо число 12
Якщо b = 3, тоді маємо ka = 10a/3 + 1, ka = 10/3a + 1, a(k – 10/3) = 1, a = 1/(k – 10/3), не існує к, при якому а буде цілим числом, тому не підходить.
Міркуючи аналогічно отримаємо решта чисел.
Відповідь: 11, 12, 15, 24, 36.
