Завдання 1020

За першу половину ночі температура змінилася на – З °С, а за другу — на – 2 °С. На скільки градусів змінилася температура за ніч?

Розв'язання

–3° + –2° = –5°

Відповідь: на –5°.

 

1) –1/8 + (–15/8) = –(1/8 + 15/18) = –16/8 = –13/4

2) –4/9 + (–3/5) = –(20/45 + 27/45) = –47/45 = –1 2/45

3) –8 9/11 + (–3 7/11) = –11 16/11 = –12 5/11

4) –11/25 + (–13/30) = – (66/150 + 65/150) = –131/150

Назва міста–героя України: БУЧА

 

1) –3/16 + (–2 5/16) = –2 8/16 = –2 1/2

2) –3/7 + (–5/6) = –(18/42 + 35/42) = –53/42 = –11 1/42

3) –3 7/9 + (–2 5/9) = –6 2/9 = –5 4/3 = –6 1/3

4) –5/12 + (–2/15) = –(25/60 + 8/60) = – 33/60 = –11/20

Прізвище українського поета, мислителя, борця за незалежність України:  СТУС

 

–4,7 + (–3,92) = –(4,7 + 3,9) = –8,6

–1 1/8 + (–7) = –(1 1/8  + 7) = –8 1/8

–3/4 + (– 5/6) = –(9/12 + 10/12) = –19/12 = –1 7/12

–8/9 + (–5/9) = –(8/9 + 5/9) = –13/9 = 1 4/9

–5/8 + (–11/12) = –(15/24 + 22/24) = –37/24 = –11 3/24

–17/27 + (–2/3) = –(17/27 + 2/3) = –(17/27 + 18/27) = –35/27 = –1 8/27

 

Завдання 1028

– 8,37 + (–9,8) = –18,17

–13 + (–1 1/2) = –(13 + 1 1/2) = –14 1/2

– 2/5 + (–3/10) = –(4/10 +3/10) = –7/10

– 11/12 + (–5/12) = –(11/12 + 5/12) = –16/12 = –4/3 = – 1 1/3

– 7/9 + (–11/15) = –(35/45 + 33/45) = –68/45 = – 1 23/45

 

Завдання 1029

1) (–5,17 + (–7,92)) + (–6,27) = –13,09 + (–6,27) = –19,36

2) –5,13 + (–109,6 + (–13,19)) = –5,13 + (–122,79) = –127,92

 

Завдання  1030

1) –6,79 + (–37,5 + (–26,17)) = –6,79 + (–63,67) = –70,46

2) (–9,25 + (–4,13)) + (–2,49) = –13,38 + (–2,49) = –15,87

 

Завдання 1031 Порівняння виразів

1) –27 + (–37) < –37, бо –27 + (–37) = –(27 + 37) = – 67

3) –82 + (–11) < –83, бо –82 + (–11) = –(82 + 11) = –93

2) –39 + (–21) > –72, бо –39 + (–21) = –(39 + 21) = –60

4) –37 + (–42) = –47 + (–32), бо –37 + (–42) = –79 і –47 + (–32) = –79

 

Завдання 1032

1) –72 + (–19) < –71, бо –72 + (–19) = –(72 + 19) = –91

2) –94 + (–47) < – 139, бо –94 + (–47) = –(94 + 47) = –141

3) –87 + (–13) = –100, бо –87 + (–13) = –(87 + 13) = –100

4) –95 + (–13) > –87 + (–24), бо –95 + (–13) = –108 і –87 + (–24) = –111

 

Завдання 1033

Якщо а = 12,7; b = 13,48, тоді –а + (–b) = –12,7 + (–13,48) = –26,18

Якщо а = 1 1/2; b = 5/16, тоді –а + (–b) = –1 1/2 + (–5/16) = –(1 8/16 + 5/16) = –1 13/16

 

Завдання 1034

Якщо х = –19; у = –27,5, то х + у + (–17,2) = –19 + (–27,5) + (–17,2) = –63,7

Якщо х = –23,9; у = –37,14, то х + у + (–17,2) = –23,9 + (–37,14) + (–17,2) = –78,24

 

Завдання 1035

 1) –1 7/8 + (–7 5/9) = –(1 63/72 + 7 40/72) = –8 103/72 = –9 31/72

2) –4 11/12 + (–8 9/16)= –(4 44/48 + 8 27/48) = –12 71/48 = –13 23/48

3) –1 3/14 + (–2 4/63)= –(1 27/126 + 2 8/126) = –3 35/126 = –3 5/18

4) –2 1/2 + (–0,65) = –(2,5 + 0,65) = –3,15

5) –3 1/7 + (–2,8) = –3 1/7 + (–2 4/5) = –(3 5/35 + 2 28/35) = –5 33/35

6) –3 2/3 + (–0,6) = –3 2/3 + (–3/5) = –(3 10/15 + 9/15) = –3 19/15 = –4 4/15

 

Завдання 1036

1) –1 3/5 + (–2 5/6) = –(1 18/30 + 25/30) = –3 43/30 = –4 13/30

2)–5 7/15 + (–8 3/10) = –(5 14/30 + 8 9/30) = –13 23/30

3) –4 9/14 + (–2 4/21) = –(4 27/42 + 2 8/42) = –6 35/42 = –6 5/6

4) –0,85 + (–4 1/2) = –0,85 + (–4,5) = –5,35

5) –4 3/10 + (–1,2) = –4,3 + (–1,2) = –5,5

6) –5,15 + (– 2 1/4) = –5,15 + (–2,25) = –7,4

 

Завдання 1037

До суми чисел –7 3/4 і –5 5/6 додай число, протилежне число 1/3.

–7 3/4 + (–5 5/6) + (–1/3) = –(7 9/12 + 5 10/12 + 4/12) = –12 23/12 = –13 11/12

 

Завдання 1038

До числа, протилежного числу 3,5, додай суму чисел –1 3/14 і –1 2/7.

–3,5 + (–1 3/14 + (–1 2/7)) = –3,5 + –(1 3/11 + 1 4/14) = –3,5 + (–21/2) = –3,5 + (–2,5) = –6

 

Завдання 1039

(–2 3/8 + (–2 1/4)) + (–7 5/6 + (–2 5/12)) = –(2 3/8 + 2 2/8) + –(7 10/12 + 2 5/12) =

= –4 5/8 + (–10 1/4) = –(4 5/8 + 10 2/8) = –14 7/8

 

Завдання 1040 Добери таке число, щоб утворилася правильна рівність:

Подай у вигляді суми двох рівних доданків число:

Порівняй значення виразів:

a + b = –2 2/5 + (–3,8) = –2,4 + (–3,8) = –6,2

x + y = –5 1/4 + (–0,95) = –5,25 + (–0,95) = –6,2

Отже, а + b = x + y

 

Завдання 1044

Порівняй значення виразів:

m + n = –3 1/4 + (–1,8) = –3,25 + (–1,8) = –5,05

p + q = –2 3/4 + (–2,2) = –2,75 + (–2,2) = –4,95

Отже, m + n < p + q

 

Завдання 1045

Накресли координатну пряму, узявши за одиничний відрізок п’ять клітинок.

Познач на ній точки A (–1,2)=A(–1 1/5), S(–0,8)=S(–4/5), С(2,2)=C(2 1/5), D(1/5) і Е(–2/5)

 

Завдання 1046

Яйця в середньому містять 12,5 % білків і 12 % жирів. Скільки грамів білків і скільки грамів жирів міститься в п'яти яйцях, якщо маса одного яйця 60 г?

Розв'язання

1) 60 • 2 = 300 (г) – загальна маса 5 яєць;

2) 300 • 0,125 = 37,5 (г) – міститься білків;

3) 300 • 0,12 = 36 (г) – міститься жирів.

Відповідь: 37,5 г білків і 36 г жирів.

 

Завдання 1047

Знайди площу зафарбованої фігури.

Розв'язання

S = пr²

S = 1/2 π • 8² – π • 4² = (1/2 • 64 – 16) • π = (32 – 16) • π = 16π ≈ 16 • 3,14 = 50,24 (см²)

Відповідь: 50,24 см².

 

Завдання 1048

Щоб поштукатурити стіни кімнати, потрібно купити суху суміш із розрахунку 6 мішків суміші на 5 м² поверхні стін. Ширина кімнати — 4 м, її довжина — 5 м, а висота — 2,8 м. Кімната має одні двері й одне вікно. Ширина дверей — 1 м , висота — 2 м, ширина вікна — 2 м, висота — 1,75 м. Скільки мішків сухої суміші потрібно купити, якщо стіни штукатурять повністю, від підлоги до стелі?

Розв'язання

1) 2,8 • 4 • 2 = 22,4 (м²) – площа 2–х стін по ширині;

2) 2,8 • 5 • 2 = 28 (м²) – площа 2–х стін по довжині з дверима та вікном;

3) 28 + 22,4 = 50,4 (м²) – площа стін кімнати з дверима та вікном;

4) 1,75 • 2 = 3,5 (м²) – площа вікна;

5) 2 • 1 = 2 (м²) – площа дверей;

6) 50,4 – 3,5 – 2 = 44,9 (м²) – площа стін кімнати без дверей та вікна;

7) 44,9 : 5 ≈ 45 : 5 = 9 (р.) – стільки разів треба по 6 мішків;

8) 9 • 6 = 54 (м.) – мішків суміші потрібно купити.

Відповідь: потрібно купити 54 мішки сухої суміші.

 

Завдання 1049

Намалюй замкнену ламану лінію із шести ланок так, щоб кожну свою ланку вона перетинала один раз.

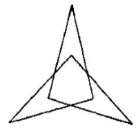
Чи існує така ламана із семи ланок? Ні. Припустимо, що існує ламана, що складається з семи ланок і яка має запропоновану властивість. Тоді в такої ламаної кількість ланок має бути удвічі більшою, ніж кількість точок перетину, тому кількість ланок є парним числом, а число 7 — непарне число.

Інші завдання дивись тут...