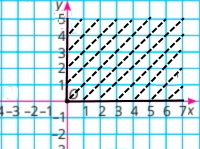
Вправа 1
Перпендикулярні прямі: Г. d і а
Вправа 2
Паралельні прямі: В. m і b
Вправа 3
Точка T лежить в третій чверті, тому В. ІІІ
Вправа 4
Координати точки M (–4; 2), тому А. М (–4; 2)
Вправа 5
Знайди площу поверхні прямокутного паралелепіпеда, виміри якого дорівнюють 4 см, 5 см і 10 см.
Розв'язання
(4 • 5 + 5 • 10 + 4 • 10) • 2 = (20 + 50 + 40) • 2 = 110 • 2 = 220 (см²)
Відповідь: Б. 220 см².
Вправа 6
Маса 1 см3 міді — 9 г. Яка маса мідного куба, якщо довжина його ребра — 5 см?
Розв'язання
1) 5 • 5 • 5 = 125 (см3) – об’єм куба;
2) 125 • 9 = 1125 (г) – маса мідного куба.
Відповідь: В. 1125 г.
Вправа 7
На малюнку 148 зображено графік залежності температури повітря (T, °С) від часу (t , год). По графіку знайди, о котрій годині температура повітря була найнижчою.
Б. о 1–й год.
Вправа 8
На малюнку 148 зображено графік залежності температури повітря (T, °С) від часу (t , год). По графіку знайди, на скільки градусів змінилася температура у проміжку часу від 2–ї год до 4–ї год.
Розв'язання
–1 – (–4) = –1 + 4 = 3 °С.
Відповідь: Г. підвищилася на З °С.
Вправа 9
Сума довжини всіх ребер прямокутного паралелепіпеда дорівнює 60 см. Знайди суму довжин трьох його ребер, що виходять з однієї вершини.
Розв'язання
60 : 4 = 15 см.
Відповідь: В. 15 см.
Вправа 10
Нижче осі абсцис лежить точка Р(207 1/2; –138,5), тому В. Р(207 1/2; –138,5)
Вправа 11
Познач на координатній площині точки (х; у) такі, що |х| ≤ 2, 0 ≤ у ≤ 3.
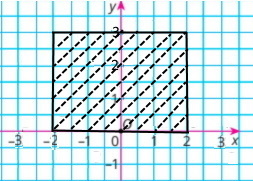
Площу фігури, що утворилася, 12 од.², тому Г. 12.
Вправа 12
Куб і прямокутний паралелепіпед мають однакові об’єми. Знайди ребро куба, якщо прямокутний паралелепіпед має виміри 2 см, 4 см і 8 см.
Розв'язання
1) 2 • 4 • 8 = 64 (см3) – об’єм паралелепіпеда і куба.
2) 64 = 43, тому ребро куба 4 (см)
Відповідь: Б. 4 см.
ЗАВДАННЯ ДЛЯ ПЕРЕВІРКИ ЗНАНЬ ДО §44 – 49
Завдання 1
a ∥ b; с ⊥ d
Завдання 2
Р – І; М – ІІ; Т – ІІІ; F – IV
Завдання 3
Знайди площу поверхні куба, ребро якого дорівнює:
|
1) 2 дм; 2 • 2 • 6 = 24 (дм²) |
2) 8 см; 8 • 8 • 6 = 384 (см²) |
Завдання 4
Координати точок: А(3; 2); В(–2; 4); С(–4; 0); D(–2; –3)
Завдання 5
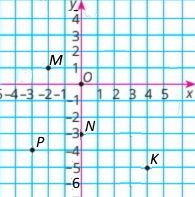
Завдання 6
Знайди об’єм прямокутного паралелепіпеда, виміри якого дорівнюють 8 см, 5 см і 1 дм.
Розв'язання
8 см • 5 см • 1 дм = 8 см • 5 см • 10 см = 400 (см3)
Відповідь: 400 см3.
Завдання 7
Об’єм прямокутного паралелепіпеда дорівнює 90 см^3. Його довжина дорівнює 6 см, висота — 3 см. Знайди:
1) суму довжин усіх ребер паралелепіпеда;
90 : (6 • 3) = 5 (см) – ширина;
4 • (6 + 5 + 3) = 4 • 14 = 56 (см) – сума довжин ребер;
2) площу поверхні паралелепіпеда.
2 • (6 • 5 + 5 • 3 + 6 • 3) = 126 (см3) – площа поверхні паралелепіпеда.
Завдання 8
У резервуарі — 4 м3 води. Щохвилини з нього виливається 0,5 м3.
1) Таблиця залежності об’єму води р (у м3), що залишається в резервуарі, від часу t (у хв).
|
t, хв |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
p, м3 |
4 |
3,5 | 3 | 2,5 | 2 | 1,5 | 1 | 0,5 | 0 |
2) Графік залежності об’єму води р від часу t.
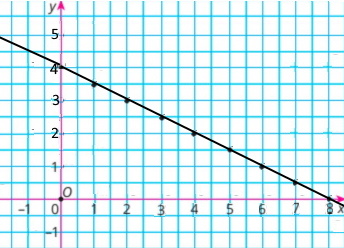
Завдання 9
Познач на координатній площині точки (х; у) такі, що:
|
1) 0 ≤ у ≤ 2, х — довільне число;
|
2) х ≤ 0, у ≥ 0.
|
Завдання 10
Прямокутний паралелепіпед і куб мають однакові об’єми. Виміри паралелепіпеда дорівнюють 8 дм, 4 дм і 2 дм. 1) Знайди ребро куба. 2) Порівняй площі поверхонь паралелепіпеда і куба. 3) Порівняй суми довжин усіх ребер паралелепіпеда і куба.
Розв'язання
1) 8 • 4 • 2 = 64 (дм3) – об’єм паралелепіпеда та куба;
2) 64 = 4^3 = 4 (дм) – ребро куба;
3) 2 • (8 • 4 + 4 • 2 + 8 • 2) = 2 • (32 + 8 + 16) = 2 • 56 = 112 (дм²) – площа поверхні паралелепіпеда;
4) 6 • 4 • 4 = 24 • 4 = 96 (дм²) – площа поверхні куба;
5) 4 • (8 + 4 + 2) = 4 • 14 = 56 (дм) – сума довжин ребер паралелепіпеда;
6) 12 • 4 = 48 (дм) – довжина ребер куба.
Відповідь: 1) 4 дм; 2) 112 дм² > 96 дм²; 3) 56 дм > 48 дм.