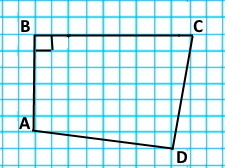
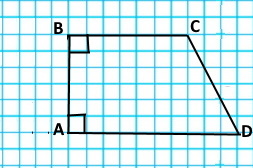
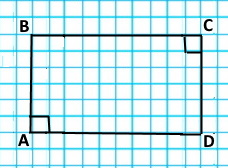
ГДЗ Істер Математика 6 клас завдання 1505 – 1521 § 44 Перпендикулярні прямі Відповіді до підручника

Завдання 1505

Прямі AB і CD називаються перпендикулярні.

Завдання 1506

m ⊥ n; s ⊥ p; t ⊥ d; g ⊥ c.

Завдання1507

Пари перпендикулярних прямих: KM ⊥ MN; MN ⊥ NP; NP ⊥ KP; KP ⊥ KM

Завдання 1508

Приклади перпендикулярних прямих з довкілля: кут будинку, стіна з підлогою, перехрестя доріг, лінії на футбольному полі.

Завдання 1509

Прямі CK i DF перпендикулярнs до прямої а.

Завдання 1510

Через точку А, що не належить прямій m, побудуй за допомогою косинця пряму n, перпендикулярну до прямої m.

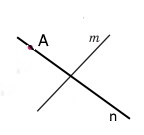
Завдання 1511

Через точку Q, що належить прямій а, побудуй за допомогою косинця пряму b, перпендикулярну до прямої а.

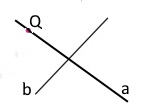
Завдання 1512

Пари перпендикулярних прямих: а ⊥ с; a ⊥ b; m ⊥ p

Завдання 1513

Накресли кут АОВ, градусна міра якого дорівнює 65°. На стороні OA познач точку К, віддалену від вершини кута на 3 см. Проведи через точку K прямі, перпендикулярні до прямих AO і BO.

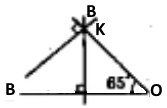
Завдання 1514

Накресли кут MKP, y градусна міра якого дорівнює 50°. На стороні KP познач точку А, віддалену від вершини кута на 2,5 см. Проведи через точку А прямі, перпендикулярні до прямих KM і KP.

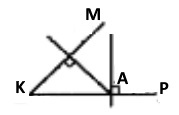
Завдання 1515

Накресли чотирикутник ABCD такий, що:

1) АВ ⊥ ВС;	2) АВ ⊥ ВС, АВ ⊥ AD;	3) АВ ⊥ AD, ВС ⊥ CD.

Завдання 1516

Накресли гострокутний трикутник ABC. Проведи через кожну його вершину пряму, перпендикулярну до протилежної сторони. Виконай відповідні записи. AM ⊥ BC; BK ⊥ AC; NC ⊥ AB

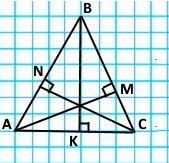
Завдання 1517

Накресли тупокутний трикутник MNK. Проведи через кожну з його вершин пряму, перпендикулярну до прямої, що містить протилежну сторону (наприклад, через вершину M проведи пряму, перпендикулярну до прямої, що містить сторону NK). Виконай відповідні записи. NB ⊥ KM; KA ⊥ MN; MC ⊥ KN

Завдання 1518

1) Між числами –5,73 і 0,8 лежать цілі числа: –5; –4; –3; –2; –1; 0

2) Між числами –14,9 і –5,7 лежать цілі числа: –14; –13; –12; –114 –10; –9; –8; –7; –6

Завдання 1519

Сплав містить дві частини цинку і п’ять частин заліза. Визнач масу сплаву, якщо заліза в ньому на 768 г більше, ніж цинку.

Розв'язання

Нехай маса одної частини х г, тоді двох —2х, п'яти — 5х г, а разом — (2х + 5х) = 7х г.

5х – 2х = 768

3х = 768

х = 768 : 3

х = 256 (г) – маса одної частини;

7 • 256 = 1792 (г) – маса сплаву.

Відповідь: 1792 г.

Завдання 1520

У 2022 році податок на прибуток становив 18 %, також із заробітної плати утримувалося 1,5 % військового збору. Зарплата Наталі 12 800 грн. Скільки вона отримає «на руки» після сплати податку та військового збору?

Розв'язання

1) 100% – 18% – 1,5% = 80,5% – становлять гроші, що отримає «на руки».

2) 12800 : 100 • 80,5 = 10304 (грн) – грошей отримає «на руки».

Відповідь: 10304 грн.

Завдання 1521

Доведи, що зі ста натуральних чисел від 1 до 100 не можна вибрати сімдесят одне число так, щоб їхня сума дорівнювала сумі інших чисел.

Розв'язання

Розіб’ємо числа на дві групи: перша – з 71 числа, друга – з 29 чисел, що залишилися.

Найменша можлива сума чисел у першій групі:

1 + 2 + 3 + … + 69 + 70 + 71 = 35 • 72 + 36 = 2556

Найбільша можлива сума у другій групі:

72 + 73 + 74 + … + 98 + 99 + 100 = 14 • 172 + 86 = 2494