
Річна контрольна робота
Варіант 1
Завдання 1
Укажи відношення, яке разом з відношенням 12 : 8 складає пропорцію.
12 : 8 = (12 : 4) : (8 : 4) = 3 : 2
|
А. 2 : 1 |
Б. 3 : 2 |
В. 4 : 3 |
Г. 5 : 4 |
Завдання 2
–1,5 + (–6,5) = –(1,5 + 6,5) = –8
|
А. 8 |
Б. –5 |
В. 5 |
Г. –8 |
Завдання 3
Укажи число, яке менше від –1,19.
|
А. –1,089 |
Б. –1,18 |
В. –1,2 |
Г. –1,175 |
Завдання 4 Середнє арифметичне чисел
(–5,8 + 2,6) : 2 = –3,2 : 2 = –1,6
|
А. 1,6 |
Б. –1,6 |
В. –3,2 |
Г. 3,2 |
Завдання 5
Знайди значення виразу:
1) |–7/20| – |1 3/5| = 7/20 – 8/5 = 7/20 – 32/20 = –25/20 = –1 5/20 = –1 1/4
2) 5 1/3 • (–2 5/8) = –16/3 • 21/8 = –2/1 • 7/1 = –14
Завдання 6
Познач на координатній площині точки А(2;–3) і В(–6;1). Знайди середину відрізка АВ – точку С. Які координати має точка С?
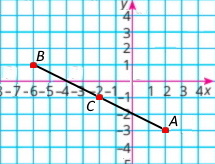
Координати середини відрізка C(–2;–1).
Завдання 7 Рівняння
6(2,5 – 1,5х) = 16,5 – 1,5(3 + 2х)
15 – 9х = 16,5 – 4,5 – 3х
15 – 9х = 12 – 3х
–9х + 3х = 12 – 15
–6х = –3
х = (–3) : (–6)
х = 1/2 = 0,5
Завдання 8
Зібрані гриби розклали в три кошики. У перший поклали 24 гриби. У другий – 5/8 від кількості грибів у першому кошику і 60% від кількості грибів у третьому. Скільки всього зібрали грибів?
Розв'язання
1) 24 : 8 • 5 = 15 (гр.) – поклали у другий кошик;
2) 15 : 0,6 = 25 (гр.) – поклали у третій кошик;
3) 24 + 15 + 25 = 64 (гр.) – зібрали всього.
Відповідь: 64 гриби.
Завдання 9
Брусок, що має форму прямокутного паралелепіпеда, потрібно пофарбувати. Виміри бруска: 60 см, 70 см, 40 см. Скільки знадобиться фарби, якщо на 1 дм поверхні витрачається 2,9 г фарби?
Розв'язання
1) S = (60 • 70 + 60 • 40 + 70 • 40) • 2 = (4200 + 2400 + 2800) • 2 =
= 18800 (см) = 188 (дм) – площа поверхні бруска;
2) 188 • 2,9 = 545,2 (г) – знадобиться фарби.
Відповідь: 545,2 г.
Варіант 2
Завдання 1 Укажи відношення, яке разом з відношенням 16 : 12 складає пропорцію.
16 : 12 = (12 : 4) : (8 : 4) = 3 : 2
|
А. 2 : 1 |
Б. 3 : 2 |
В. 4 : 3 |
Г. 5 : 4 |
Завдання 2
–2,5 + (–5,5) = –(2,5 + 5,5) = –8
|
А. 8 |
Б. 3 |
В. –3 |
Г. –8 |
Завдання 3
Укажи число, яке більше за –1,17.
|
А. –1,089 |
Б. –1,18 |
В. –1,2 |
Г. –1,175 |
Завдання 4 Середнє арифметичне чисел
(–5,9 + 2,7) : 2 = –3,2 : 2 = –1,6
|
А. 1,6 |
Б. –1,6 |
В. –3,2 |
Г. 3,2 |
Завдання 5
1) |11/20| – |1 4/5| = 11/20 – 9/5 = 11/20 – 36/20 = –25/20 = –1 5/20 = –1 1/4
2) –1 5/7 • (–9 1/3) = 12/7 • 28/3 = 4/1 • 4/1 = 16
Завдання 6
Познач на координатній площині точки С(–4;5) і D(2;–1). Знайди середину відрізка CD – точку M. Які координати має точка M?
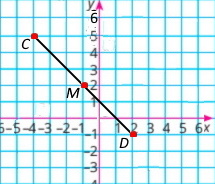
Координати середини відрізка M(–1;2).
Завдання 7
6(1,5 – 2,5х) = 24,5 – 3,5(5 + 2х)
9 – 15х = 24,5 – 17,5 – 7х
9 – 15х = 7 – 7х
–15х + 7х = 7 – 9
–8х = –2
х = (–2) : (–8)
х = 1/4 = 0,25
Завдання 8
Моток дроту розрізали на три частини. Довжина першої частини – 48 м. довжина другої становила 3/8 від довжини першої частини та 60% від довжини третьої. Скільки метрів дроту було в мотку?
Розв'язання
1) 48 : 8 • 3 = 18 (м) – довжина другої частини дроту;
2) 18 : 0,6 = 30 (м) – довжина третьої частини дроту;
3) 48 + 18 + 30 = 96 (м) – дроту було в мотку.
Відповідь: 96 м.
Завдання 9
Виміри бруска, що має форму прямокутного паралелепіпеда, становлять 80 см, 30 см і 50 см. Цей брусок потрібно пофарбувати. Скільки знадобиться фарби, якщо на 1 дм поверхні витрачається 2,8 г фарби?
Розв'язання
1) S = (80 • 30 + 80 • 50 + 50 • 30) • 2 = (2400 + 4000 + 1500) • 2 = 15800 (см) =
= 158 (дм) – площа поверхні бруска;
2) 158 • 2,8 = 442,4 (г) – знадобиться фарби.
Відповідь: 442,4 г.
Варіант 3
Завдання 1
Укажи відношення, яке разом з відношенням 15 : 12 складає пропорцію.
15 : 12 = (15 : 3) : (12 : 3) = 5 : 4
|
А. 5 : 4 |
Б. 4 : 3 |
В. 3 : 2 |
Г. 2 : 1 |
Завдання 2
–2,5 + (–6,5) = –(2,5 + 6,5) = –9
|
А. 9 |
Б. –9 |
В. 4 |
Г. –4 |
Завдання 3
Укажи число, яке більше за –3,16.
|
А. –3,17 |
Б. –3,168 |
В. –3,09 |
Г. –3,2 |
Завдання 4
Знайди середнє арифметичне чисел –5,7 і 2,3.
(–5,7 + 2,3) : 2 = –3,4 : 2 = –1,7
|
А. –1,7 |
Б. 1,7 |
В. –3,4 |
Г. 3,4 |
Завдання 5
1) |–7/12| – |1 3/4| = 7/12 – 7/4 = 7/12 – 21/12 = –14/12 = –1 2/12 = –1 1/6
2) –2 2/5 • 8 1/3 = –12/5 • 25/3 = –4/1 • 5/1 = –20
Завдання 6
Познач на координатній площині точки M(4;–5) і N(–2;1). Знайди середину відрізка MN – точку P. Які координати має точка P?
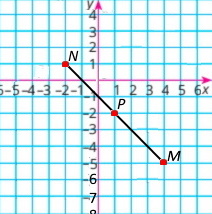
Координати середини відрізка P(1;–2)
Завдання 7 Рівняння
8(3,5 – 1,5х) = 35,5 – 1,5(7 + 2х)
28 – 12х = 35,5 – 10,5 – 3х
28 – 12х = 25 – 3х
–12х + 3х = 25 – 28
–9х = –3
х = (–3) : (–9)
х = 3/9 = 1/3
Завдання 8
На першій ділянці росте 36 кущів троянд. Кількість кущів, що ростуть на другій ділянці, становить 3/4 від кількості кущів першої ділянки та 90% від кількості кущів третьої. Скільки кущів троянд росте на трьох ділянках разом?
Розв'язання
1) 36 : 4 • 3 = 27 (к.) – росте на другій ділянці;
2) 27 : 0,9 = 30 (к.) – росте на третій ділянці;
3) 36 + 27 + 30 = 93 (к.) – росте на трьох ділянках разом.
Відповідь: 93 кущі троянд.
Завдання 9
Брусок, що має форму прямокутного паралелепіпеда, потрібно пофарбувати. Виміри бруска: 50 см, 60 см і 40 см. Скільки знадобиться фарби, якщо на 1 дм поверхні витрачається 2,8 г фарби?
Розв'язання
1) S = (50 • 60 + 50 • 40 + 60 • 40) • 2 = (3000 + 2000 + 2400) • 2 = 7400 • 2 =
= 14800 (см ) = 148 (дм ) – площа поверхні бруска;
2) 148 • 2,8 = 414,4 (г) – знадобиться фарби.
Відповідь: 414,4 г.
Варіант 4
Завдання 1
Укажи відношення, яке разом з відношенням 18 : 12 складає пропорцію.
18 : 12 = (18 : 6) : (12 : 6) = 3 : 2
|
А. 5 : 4 |
Б. 4 : 3 |
В. 3 : 2 |
Г. 2 : 1 |
Завдання 2
–1,5 + (–7,5) = –(1,5 + 7,5) = –9
|
А. 9 |
Б. –9 |
В. –6 |
Г. 6 |
Завдання 3
Укажи число, яке менше від –3,18.
|
А. –3,17 |
Б. –3,168 |
В. –3,09 |
Г. –3,2 |
Завдання 4 Середнє арифметичне чисел
(–5,8 + 2,4) : 2 = –3,4 : 2 = –1,7
|
А. –1,7 |
Б. 1,7 |
В. –3,4 |
Г. 3,4 |
Завдання 5
1) |5/12| – |–1 3/4| = 5/12 – 7/4 = 5/12 – 21/12 = –16/12 = –1 4/12 = –1 1/3
2) –5 1/4 • (–2 2/3) = 21/4 • 8/3 = 7/1 • 2/1 = 14
Завдання 6
Познач на координатній площині точки K(5;–3) і L(–1;5). Знайди середину відрізка KL – точку C. Які координати має точка C?
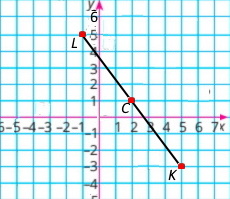
Координати середини відрізка C(2;1)
Завдання 7 Рівняння
4(2,5 – 3,5х) = 19,5 – 2,5(5 + 2х)
10 – 14х = 19,5 – 12,5 – 5х
10 – 14х = 7 – 5х
–14х + 5х = 7 – 10
–9х = –3
х = (–3) : (–9)
х = 3/9 = 1/3
Завдання 8
Перший цех виготовив 32 прилади. Кількість приладів, виготовлених другим цехом, становила 7/8 від кількості, що виготовив перший цех, та 70% від кількості, що виготовив третій. Скільки приладів виготовили три цехи разом?
Розв'язання
1) 32 : 8 • 7 = 28 (пр.) – виготовив другий цех;
2) 28 : 0,7 = 40 (пр.) – виготовив третій цех;
3) 32 + 28 + 40 = 100 (пр.) – виготовили три цехи разом.
Відповідь: 100 приладів.
Завдання 9
Виміри бруска, що має форму прямокутного паралелепіпеда, становлять 70 см, 50 см і 40 см. Цей брусок потрібно пофарбувати. Скільки знадобиться фарби, якщо на 1 дм поверхні витрачається 2,9 г фарби?
Розв'язання
1) S = (70 • 50 + 70 • 40 + 50 • 40) • 2 = (3500 + 2800 + 2000) • 2 = 8300 • 2 =
= 16600 (см) = 166 (дм) – площа поверхні бруска;
2) 166 • 2,9 = 481,4 (г) – знадобиться фарби.
Відповідь: 481,4 г.