Інші завдання дивись тут...

Діагностична (контрольна) робота ДР–10

Перпендикулярні і паралельні прямі. Координатна площина. Графіки. Прямокутний паралелепіпед. Куб 

Варіант 1

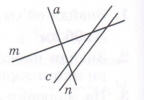
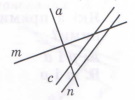
Завдання 1 Паралельні прямі

А. c i a Б. m i n В. a i m Г. c i n

Завдання 2

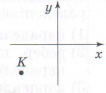
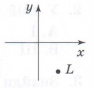
У якій чверті лежить точка К на малюнку?

А. Ⅰ Б. Ⅱ В. Ⅲ Г. Ⅳ

Завдання 3

Знайди площу поверхні куба з ребром 5 см.

А. 20 см² Б. 25 см² В. 100 см² Г. 150 см²

Розв'язання S = 6 • а² = 6 • 5² = 150 (см²) Відповідь: 150 см².

Завдання 4

Укажи точку, що належать осі ординат.

Коли х = 0, точка належить осі ординат

А. (0;–8)

Б. (–1;1)

В. (5;5)

Г. (–6;0)

Завдання 5

Знайди об’єм прямокутного паралелепіпеда, виміри якого – 4 дм, 6 дм і 1 м.

Розв'язання 

V = abc = 4 • 6 • 10 = 240 (дм³).

Відповідь: 240 дм³.

 

Завдання 6

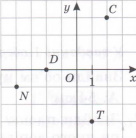
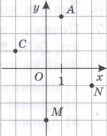
Знайди координати точок на малюнку.

С(2;3); D(–2;0); N(–4;–1); T(1;–3)

Завдання 7

Познач на координатній площині точки А(–3;1); B(–6;–2); C(7;–1); D(1;2).

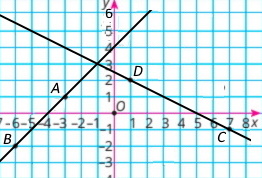
Знайди координати точки перетину:

1) прямих АВ і CD; (–1;3)

2) прямої CD з віссю абсцис; (5;0)

3) прямої АВ з віссю ординат. (0;4)

 

Завдання 8

Об’єм прямокутного паралелепіпеда – 120 см , довжина – 6 см, а висота – 4 см. Знайди суму довжини усіх його ребер.

Розв'язання

V = abc

120 = a • 6 • 4

120 = 24a

a = 120 : 24

a = 5 (см) – ширина паралелепіпеда;

(а + b + c) • 4 = (5 + 6 + 4) • 4 = 15 • 4 = 60 (см) – сума довжин усіх ребер.

Відповідь: 60 см.

 

Завдання 9

У баку – 20 м води. Щохвилини з нього виливається 4 м води.

1) Склади таблицю залежності об’єму води p (у м), що залишається в баку, від часу t (у хв).

t, хв	0	1	2	3	4	5
p, м3	20	16	12	8	4	0

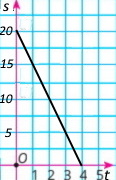
2) Побудуй графік залежності об’єму води p від часу t.

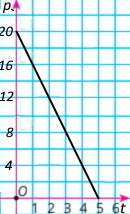
Варіант 2

Завдання 1 Перпендикулярні прямі

А. c i a Б. m i n В. a i m Г. c i n

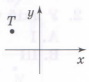
Завдання 2

У якій чверті лежить точка Т на малюнку?

А. Ⅰ Б. Ⅱ В. Ⅲ Г. Ⅳ

Завдання 3

Знайди площу поверхні куба, ребро якого – 3 см.

А. 9 см² Б. 12 см² В. 54 см² Г. 36 см²

Розв'язання S = 6 • а² = 6 • 3² = 54 (см²) Відповідь: 54 см².

Завдання 4 

Укажи точку, що належать осі абсцис.

Коли у = 0, точка належить осі абсцис.

А. (0;–8)

Б. (–1;1)

В. (5;5)

Г. (–6;0)

Завдання 5

Знайди об’єм прямокутного паралелепіпеда, виміри якого – 1 м, 4 дм і 5 дм.

Розв'язання 

V = abc = 10 • 4 • 5 = 200 (дм³)

Відповідь: 200 дм³.

 

Завдання 6

Знайди координати точок на малюнку.

А(3;1); М(0;4); L(–3;2); T(–2;–2)

Завдання 7 

Познач на координатній площині точки D(5;2); C(–4;–1); B(6;–3); A(–1;4). Знайди координати точки перетину:

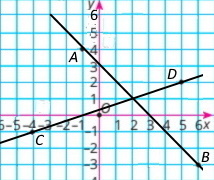
1) прямих АВ і CD; (2;1)

2) прямої CD з віссю абсцис; (–1;0)

3) прямої АВ з віссю ординат. (0;3)

 

Завдання 8

Об’єм прямокутного паралелепіпеда – 72 дм , довжина – 6 дм, ширина – 3 дм. Знайди суму довжини усіх його ребер.

Розв'язання

V = abc

72 = 3 • 6 • с

72 = 18с

с = 72 : 18

с = 4 (см) – висота паралелепіпеда;

(а + b + c) • 4= (3 + 6 + 4) • 4 = 13 • 4 = 52 (дм) – сума довжин усіх ребер.

Відповідь: 52 дм.

 

Завдання 9

Пішохід перебуває на відстані 15 км від села і рухається до нього. Щогодини пішохід проходить 3 км.

1) Склади таблицю залежності відстані s (у км), до села від часу t (у год).

t, год	0	1	2	3	4	5
s, км	15	12	9	6	3	0

2) Побудуй графік залежності відстані до села s від часу t.

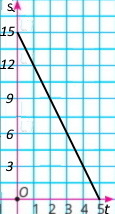
Варіант 3

Завдання 1 Перпендикулярні прямі

А. p i a Б. b i a В. m i p Г. b i m

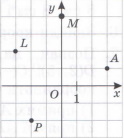
Завдання 2

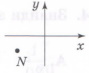
У якій чверті лежить точка L на малюнку?

А. Ⅰ Б. Ⅱ В. Ⅲ Г. Ⅳ

Завдання 3

Знайди площу поверхні куба, ребро якого – 7 дм.

А. 294 дм² Б. 49 дм² В. 28 дм² Г. 196 дм²

Розв'язання S = 6 • а² = 6 • 7² = 294 (дм²) Відповідь: 294 дм².

Завдання 4

Укажи точку, що належать осі абсцис.

Коли у = 0, точка належить осі абсцис

А. (3;3)

Б. (0;–7)

В. (–9;0)

Г. (2;–2)

Завдання 5

Знайди об’єм прямокутного паралелепіпеда, виміри якого – 6 см, 8 см і 1 дм.

Розв'язання 

V = abc = 6 • 8 • 10 = 480 см³

Відповідь: 480 см³.

 

Завдання 6 Координати точок

А(1;3); C(–2;1); M(0;–3); N(3;–1)

Завдання 7

Познач на координатній площині точки D(2;5); C(–5;–2); B(5;–1); A(–3;3). Знайди координати точки перетину:

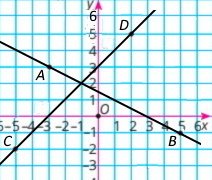
1) прямих АВ і CD; (–1;2)

2) прямої AB з віссю абсцис; (3;0)

3) прямої CD з віссю ординат. (0;3)

 

Завдання 8

Об’єм прямокутного паралелепіпеда – 90 м , ширина – 5 м, висота – 6 м. Знайди суму довжини усіх його ребер.

Розв'язання

V = abc

90 = 5 • b • 6

90 = 30b

b = 90 : 30

b = 3 (м) – довжина паралелепіпеда;

(а + b + c) • 4 = (5 + 3 + 6) • 4 = 14 • 4 = 56 (м) – сума довжин усіх ребер.

Відповідь: 56 м.

 

Завдання 9

У басейні – 24 м³ води. Щохвилини з нього виливається 6 м води.

1) Склади таблицю залежності об’єму води p (у м³), що залишилася в резервуарі, від часу t (у хв).

t, хв	0	1	2	3	4
p, м3	24	18	12	6	0

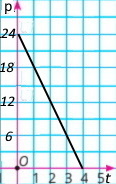
2) Побудуй графік залежності об’єму води p від часу t.

Варіант 4

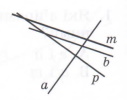
Завдання 1 Паралельні прямі

А. p i a Б. b i a В. m i p Г. b i m

Завдання 2

У якій чверті лежить точка N на малюнку?

А. Ⅰ Б. Ⅱ В. Ⅲ Г. Ⅳ

Завдання 3

Знайди площу поверхні куба, ребро якого – 2 дм.

А. 16 дм² Б. 8 дм² В. 24 дм² Г. 4 дм²

Розв'язання S = 6 • а² = 6 • 2² = 24 (дм²) Відповідь: 24 дм².

Завдання 4

Укажи точку, що належать осі ординат.

Коли х = 0, точка належить осі ординат

А. (3;3)

Б. (0;–7)

В. (–9;0)

Г. (2;–2)

Завдання 5

Знайди об’єм прямокутного паралелепіпеда, виміри якого – 1 дм, 5 см і 7 см.

Розв'язання 

V = abc = 10 • 5 • 7 = 350 см³

Відповідь: 350 см³.

 

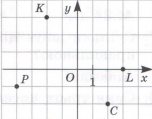
Завдання 6 Координати точок

L(3;0); K(–2;3); P(–4;–1); C(2;–2)

Завдання 7

Познач на координатній площині точки A(–2;4); B(3;–1); C(–3;–1); D(1;7). Знайди координати точки перетину:

1) прямих АВ і CD; (–1;3)

2) прямої AB з віссю абсцис; (2;0)

3) прямої CD з віссю ординат. (0;5)

 

Завдання 8

Об’єм прямокутного паралелепіпеда – 60 дм , довжина – 5 дм, ширина – 4 дм. Знайди суму довжини усіх ребер цього паралелепіпеда.

Розв'язання

V = abc

60 = 4 • 5 • с

60 = 20с

с = 60 : 20

с = 3 дм – довжина паралелепіпеда;

(а + b + c) • 4 = (4 + 5 + 3) • 4 = 12 • 4 = 48 дм – сума довжин усіх ребер.

Відповідь: 48 дм.

 

Завдання 9

Турист перебуває на відстані 20 км від табору і рухається до нього. Щогодини турист проходить 5 км.

1) Склади таблицю залежності відстані s (у км) до табору від часу t (у год).

t, год	0	1	2	3	4
s, км	20	15	10	5	0

2) Побудуй графік залежності відстані до табору s від часу t.

Інші завдання дивись тут...