ГДЗ Математика 6 клас Бевз завдання 72 – 108 §3 КООРДИНАТНА ПЛОЩИНА відповіді до підручника

Інші завдання дивись тут...

Завдання 72

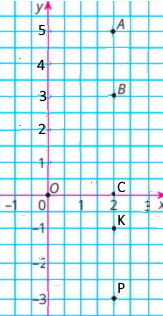
а) A(2;1), X(3;1), M(1;0), D(0;1), С(-2;1), K(-3;0) S(-2;0), P(-2;-2), T(1;-1), B(3;-1)

б) точка К має ординату — 0, точка Р — -2, точка Т — -1, точка Х — 1.

в) 0 абсциса точки D, що належать осі ординат.

г) Від'ємні абсциси иають точки С, К, S, Р

ґ) Недодатні ординати точок Р, Т, В

Завдання 73

На осі абсцис лежать точка Б

Завдання 74

У другій чверті лежить точка В

Завдання 75

Координати точок: (-4;0), (2;0), (0;-2)

Завдання 76

а) L(2;2), A(4;3), P(6;1), D(0;5), K(-2;5), C(-4;0), E(-2;-4), F(3;-3), B(8;-1)

б) A(1;1,5); R(3;2), M(1;0), C(2;0), E(0;2), N(0;1), T(-1;2), D(-2;0), B(-1;-1), F(0;-2), S(3;-1)

Завдання 77

Завдання 78

Точки лежать на одній прямій.

Завдання 79

Точки лежать на одній прямій.

Висновок: точки лежать на одній прямій, бо ординати точок однакові і дорівнюють 2.

Завдання 80

Проходить через точку Т(-3,1) і не проходить через точку М(-2,0)

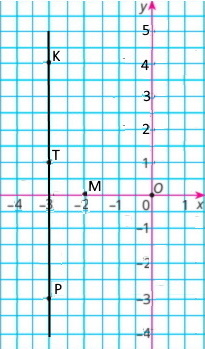
Завдання 81

Не проходить через точку К(1,2)

Завдання 82

АВ = 5 – (-2) = 7 (од. відр.)

Завдання 83

Координата точки М(-4;-3); Відстань КМ = 1 од. відр.

Завдання 84

Ближче до початку координат розташована точка: А(0;5), бо АО = 5 од. відр., ОВ = 6 од. відр., 5 < 6

Завдання 85

Довжина ламаної: 3 + 2 + 4 + 3 = 12 од. в.

Завдання 86

Довжина ламаної: 2 + 4 + 3 + 4 = 13 од. в.

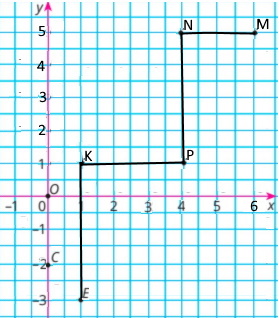
Завдання 87

Вийшла фігура квадрат.

а) точки перетину сторін фігури з осями координат:

з віссю Ох: (-1;0) і (3;0); З віссю Оу: (0;1) і (0;-3)

б) точка перетину відрізків АС і BD. (1;-1)

Завдання 88

Покажи, як перегинанням аркуша паперу можна утворити: а) перпендикулярні відрізки; б) паралельні відрізки.

Завдання 89

Точки А(-2;-2), B(1;1) і С(4;4) лежать на одній прямій, бо абсциси і ординати точок змінюються на однакову величину.

Так, кожна точка цієї прямої має ординату, що дорівнює абсцисі.

Завдання 90

а) червоним кольором точки А(2;4), 6(1;5), С(3;1); (I чверть)

б) зеленим — точки К(-4;2), Р(-2;3), S(-2;2); (II чверть)

в) синім — L(1;-5), Q(-4;-4), N(-2;-3); (III чверть)

г) жовтим — М(3;-1), F(2;-4), Z(1;-1). (IV чверть)

Ми помітили, що кожні три точки лежать в різних чвертях.

Завдання 91

а) додатну абсцису і від'ємну ординату містять точки IV чверті координатної площини.

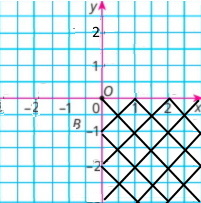
б) від'ємну абсцису і додатну ординату містять точки ІI чверті координатної площини.

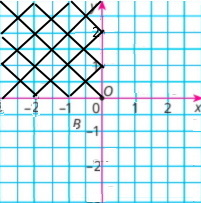
Завдання 92

а) додатну абсцису і додатну ординату містять точки I чверті координатної площини.

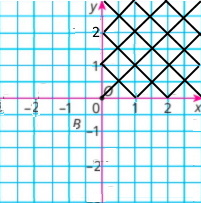
б) від'ємну абсцису і від'ємну ординату містять точки III чверті координатної площини.

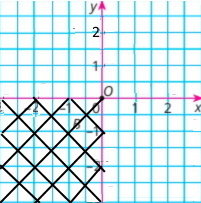
Завдання 93

Через точку М(4;-3) провели прямі, які перпендикулярні до осей координат.

Координати точок перетину цих прямих з віссю абсцис (4;0) і віссю ординат (0:-3)

Завдання 94

Три вершини прямокутника ABCD мають такі координати: А(-2;2), В(4;2), С(4;-3). Знайди координати точки D, а також його периметр і площу, вважаючи, що довжина одиничного відрізка дорівнює 1 см.

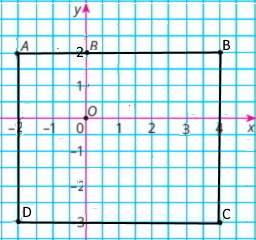
Розв'язання

Координата точки D(-2;-3).

AB = 4 – (–2) = 6 cм – довжина сторони АВ;

ВС = 2 – (–3) = 5 см – довжина сторони ВС;

1) S = 5 • 6 = 30 (см²) – площа прямокутника;

2) Р = (5 + 6) • 2 = 22 (см) – периметр прямокутника.

Відповідь: 30 см², 22 см.

Завдання 95

Точки А(1; 0), В(1; 3), С(5; 3) — три вершини прямокутника ABCD. Знайди координати четвертої вершини прямокутника, а також його периметр і площу, вважаючи, що довжина одиничного відрізка дорівнює 1 см.

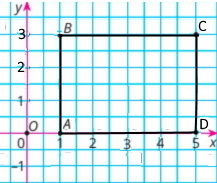
Розв'язання

Координата точки D(5;3).

1) Р = (3 + 4) • 2 = 14 (см) – периметр прямокутника;

2) S = 3 • 4 = 12 (см²) – площа прямокутника;

Відповідь: 14 см; 12 см².

Завдання 96

На малюнку т. А симетрична т. В відносно т. М. Покажи, що:

а) точки А(0;5) і В(0;1)

1) симетричні відносно точки М(0;3)

Точка М(0;3) це — середина відрізка

АВ ((0 + 0) : 2 = 0 і (5 + 1) : 2 = 3)

б) точки К(-3;2) і Р(3;2)

2) симетричні відносно точки Т(0;2)

Точка Т(0;2) — це середина відрізка

КР ((3 + (-3)) : 2 = 0 і (2 + 2) : 2 = 2)

Завдання 97

Точка К симетрична точці С(-3;2) відносно точки М(1;2).

Координати точки: К(5;2)

Завдання 98

Точка P(4;-7) симетрична точці A(-4;7) відносно початку координат.

Точка F(6;-1) симетрична відносно точки М(1;3).

Завдання 99

Точки А і В називають симетричними відносно прямої а, якщо пряма а перпендикулярна до відрізка АВ і проходить через його середину. Чи симетричні відносно осі абсцис точки А(2; 4) і В(2; -4)? Так, бо середина відрізка AB точка з координатами (2;0), тобто ордината дорівнює 0.

Точки симетричні точкам А і В відносно осі ординат: А₁(-2;4) і В₁(-2;-4)

Завдання 100

На координатній площині точка К, симетрична точці С(-2;-3) відносно осі х, і точка Р, симетрична точці С відносно осі у.

Координати точок: К(-2:3) і Р(2:-3)

Завдання 101

На координатній площині точка К, симетрична точці Р(3;-5) відносно осі х, і точка Е, симетрична точці Р відносно осі у.

Координати точок: К(3;5) і Е(-3;-5)

Завдання 102

а) (3 • 6) : 2 = 9 (см²) – площа трикутника з вершинами А(0; 3), 0(0;0) і В(6;0);

б) (3 • 3) : 2 = 4,5 (см²) – площа трикутника з вершинами К(-1;1), Р(4;1) і Т(4;4).

Завдання 103

а) (5 • 5) : 2 = 5

б) (5 – 5) • 5 = 0

в) 5 – (5 : 5) = 4

Завдання 104

Чи існує прямокутний паралелепіпед, довжини ребер і площа поверхні якого виражаються непарними числами? Ні, не існує такого паралелепіпеда. Якщо довжини ребер виражаються непарними числами, то площа кожної грані буде непарним числом, як добуток двох непарних чисел, але площа поверхні буде сумою шести непарних чисел, що в результаті дасть парне число. Тому неможливо, щоб довжини ребер і площа поверхні одночасно виражалися непарними числами.

Завдання 105

Найменше значення може мати вираз х² + 16 якщо х² = 0, тому х = 0

Найменше значення може мати вираз (х + 16)², якщо х + 16 = 0, тому х = -16

Вправи для повторення

Завдання 106