Завдання 109 Модуль числа
|
|6| = 6
|
|-9| = 9
|
|-37| = 37
|
|4 500 789| = 4 500 789
|
|0| = 0
|
Завдання 110
Н.в. модуль
Р.в. модуля
Д.в. модулю, модулеві
З.в. модуль
О.в. модулем
М.в. в модулі, по модулю
Кл.в. модулю
Завдання 111
А Якщо модулі 2 різних чисел рівні, то числа протилежні. Так
Б Числа з нерівними модулями не можуть бути протилежними. Так
В Якщо модулі двох чисел рівні, то ці числа рівні або протилежні. Так
Завдання 112
|
а) |-3| + |3| = 3 + 3 = 6
б) |-2| • |-З| = 2 • 3 = 6
|
в) |5| • |-4| = 5 • 4 = 20
г) |-2| + |-7| = 2 + 7 = 9
|
д) |-4| • |-15| = 4 • 15 = 60
е) |-18| : |-9| = 18 : 9 = 2
|
Завдання 113
Г |-1| > |-3|
Завдання 114
1 Сума модулів — Б 8
2 Різниця модулів — В 4
3 Добуток модулів — Г 12
4 Частка модулів — А 3
Завдання 115
|
1) 120
|
2) 1500
|
Завдання 116
|-7| = 7
Завдання 117
Так, відстань між точками А(-8) і О(О) дорівнює |-8|, бо |-8| = 8
а) відстань між точками О(О) і 6(8) дорівнює 8
6) відстань між точками С(-5) і 6(5) дорівнює 10
Завдання 118
Точка Р(-12) розташована ближче до точки О, бо |-12| = 12 і |-8| = 8, а 12 > 8, тому |-12| > |-8|
Завдання 119
а) 5 • |7| + 4 = 5 • 7 + 4 = 35 + 4 = 39
б) 100 • |-13| – 45 = 100 * 13 – 45 = 1300 - 45 = 1255
в) |-27| : 3 + 49 = 27 : 3 + 49 = 9 + 49 = 58
г) 56 – |-3| • |8| = 56 – 3 • 8 = 56 - 24 = 32
г) |-8| • |-4| – |-56| : 7 = 8 • 4 – 56 : 7 = 32 – 8 = 24
Завдання 120
а) |-2| • 80 – 8 = 2 • 80 – 8 = 160 – 8 = 152
б) 144 : |12| + |0| = 144 : 12 + 0 = 12
в) 15 • |4| – |-45| = 15 • 4 – 45 = 60 – 45 = 15
г) 600 – |-6| • |7| = 600 – 6 • 7 = 600 – 42 = 558
ґ) |-45|:|-5| + |3| • |-12| = 45 : 5 + 3 • 12 = 9 + 36 = 45
Завдання 121
а) Якщо х = 7, тоді 83 + |-х| • 7 = 83 + |-7| • 7 = 132
б) Якщо х = -5, тоді 83 + |-х| • 7 = 83 + |-(-5)| • 7 = 118
в) Якщо х = 0, тоді 83 + |-х| • 7 = 83 + |0| • 7 = 83
Завдання 122
Якщо |-х|= 203, тоді |х|= 203, а х = 203 або х = -203
Завдання 123 Рівняння
а) |х|= -1; Не існує розв'язку, бо модуль кожного числа - число невід'ємне.
б) |х|= 2; х = 2 або х = -2
в) |х|= 5. х = 5 або х = -5
Завдання 124
а) |х|= 6; х = 6 або х = -6
б) |х|= 8; х = 8 або х = -8
в) |х|= 0. х = 0
Завдання 126
а) 4|13| – |-4| – |-13| = 4 • 13 – 4 – 13 = 54 – 4 – 13 = 35
б) |50•(-20)| + 2|(-6)| – 57 = 50 • 20 + 2 • 6 – 57 = 1000 + 12 – 57 = 955
в) |5 + 14| – |5 - 2| + З • 5 • 2 = 19 – 3 + 30 = 46
Завдання 127
Існує 9 цілих чисел, які задовольняють нерівність |х| < 5
Завдання 128
Існує 11 натуральних чисел, які задовольняють нерівність |х|<12:
1, 2, 3, 4, 5, 6, 7, 8, 9, 10, 11
Цілих від'ємних чисел 11: -1, -2,-3, -4, -5, -6, -7, -8, -9, -10, -11
Всього цілих чисел 23: -11, -10, -9, ..., -1, 0, 1, ..., 9, 10, 11
Завдання 129
|
а) |х| – 6 = 4
|х| = 4 + 6
|х| = 10
х = 10 або х = -10
|
б) |х| + 2 = 3
|х| = 3 – 2
|х| = 1
х = 1 або х = -1
|
в) 3|х| – 7 = 5
3|х| = 12
|х| = 12 : 3
|х| = 4
х = 4 або х = -4
|
Завдання 130
|
а) |а| + 7 = 11
|а| = 11 – 7
|а| = 4
а = 4 або х = -4
|
б) 16 – |с| = 13
|с| = 16 – 13
|с| = 3
с = 3 або с = -3
|
в) 2|х| – 10 = 8
2|х| = 18
|х| = 18 : 2
|х| = 9
х = 9 або х = -9
|
Завдання 131
Побудуйте в системі координат точку А(х; у) і точки з координатами (|х|;у), (х;|у|), (|x|;|y|), якщо:
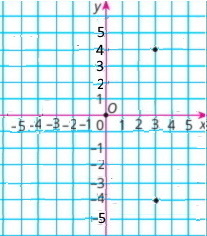
а) якщо х = 3, у =-4, тоді A(3;-4);
Точка А і точка з координатами (|3|;-4) = (3;-4) співпадають.
Точки з координатами: (3;|-4|) = (3;4) і (|3|;|4|) = (3;4) співпадають.
Симетричні відносно осі Ох точки з координатами (3;4) і (3;-4)
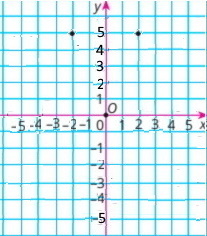
б) якщо х = -2, у = 5, тоді А(-2;5)
Точки з координатами (|-2|;5) = (2;5) і (|-2|;|5|) = (2;5) співпадають
Точка А і точка з координатою (-2;|5|) = (-2;5) співпадають
Симетричні відносно осі Оу точки з координатами (-2;5) і (2;5)
Завдання 132
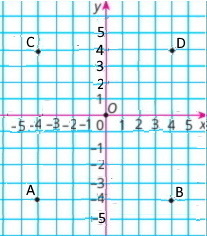
Побудуй у системі координат точку А(х; у) і точки В(|х|;у), С(х;|у|), D(|x|;|у|), якщо:
а) якщо х = -5; у = -3, тоді А(-5;-3); В(|-5|;-3) = В(5;-3); С(-5;|3|)= С(-5;3), D(|-5|;|-3|) = D(5;3)

б) якщо х = -4, у = -4, тоді А(-4;-4); В(|-4|;-4) = В(4;-4); С(-4;|4|)= С(-4;4), D(|-4|;|-4|) = D(4;4)
Завдання 133
Подумай, як можна розрізати куб на 6 однакових чотирикутних піраміди.
Завдання 134
Більший із двох квадратів розрізали на 4 трикутники. Як із них і меншого квадрата скласти один великий квадрат?
Завдання 135
Карлсон купив 15 тістечок по 10 крон і по 14 крон, заплативши всього 190 крон. Скільки тістечок кожного виду купив Карлсон?
Розв'язання
Нехай по 14 крон Карлсон купив х тістечок, тоді по 15 крон — (15 - х) тістечок, а їх вартість відповідно 14х грн і 10 • (15 - х) грн. Складаємо рівняння.
14х + 10 • (15 – х) = 190
14х + 150 – 10х = 190
14х – 10х = 190 – 150
4х = 40
х = 40 : 4
х = 10 (т.) – тістечок по 14 крон;
15 – 10 = 5 (т.) – тістечок по 15 крон.
Відповідь: 10 тістечок і 5 тістечок.
Вправи для повторення
Завдання 136
|
а) (х – 5)(х – 7) = 0
х – 5 = 0 або х – 7 = 0
х = 5 або х = 7
|
б) Зх(х – 4) = 0
3х = 0 або х - 4 = 0
х = 0 або х = 4
|
Завдання 137
У трьох ящиках 40 кг помідорів, причому в першому на 2 кг більше, ніж у другому, і на 3 кг менше, ніж у третьому. Скільки кілограмів помідорів у кожному ящику?
Розв'язання
Нехай у першому ящику х кг, тоді у другому — (х - 2) кг, а у третьому — (х + 3) кг. Складаємо рівняння.
х + (х – 2) + (х + 3) = 40
3х + 1 = 40
3х = 40 – 1
3х = 39
х = 39 : 3
х = 13 (кг) – у першому ящику;
13 – 2 = 11 (кг) – у другому ящику;
13 + 3 = 16 (кг) – у третьому ящику.
Відповідь: 13 кг, 11 кг, 16 кг.
Завдання 138
Побудуй траєкторію спрайта після виконання частини коду.