Завдання 228
|
10, 11, 12 |
999, 1000, 1001 |
–1, 0, 1 |
–3, –2, –1 |
–15, –14, –13 |
Завдання 229
|
а) 5 – 2 = 3
2 – 5 = –3
0 – 8 = –8
|
б) –3 – 1 = –4
–1 – 3 = –4
–6 – 0 = –6
|
в) 2 – (–3) = 5
5 – (–19) = 14
0 – (–8) = 8
|
г) –1 – (–7) = 6
–9 – (–5) = –4
0 – 0 = 0
|
Завдання 230
|
–5 – 2 = –7
|
2 – 3 = –1
|
Завдання 231
|
а
|
7
|
4
|
0
|
–2
|
–7
|
–3
|
–29
|
1
|
|
b
|
3
|
9
|
10
|
1
|
8
|
5
|
–5
|
–9
|
|
a – b
|
4
|
–5
|
–19
|
–3
|
–15
|
–8
|
–24
|
10
|
|
7 – 3 = 4
4 – 9 = –5
|
0 – 19 = –19
–2 – 1 = –3
|
–7 – 8 = –15
–3 – 5 = –8
|
–29 – (–5) = –24
1 – (–9) = 10
|
|||||
Завдання 232
|
–12 – 3 = –15
–6 – 3 = –9
|
–8 – 3 = –11
–11 – 3 = –14
|
–5 – 3 = –8
–1 – 3 = –4
|
0 – 3 = –3
|
Завдання 233
|
–7 – х = –20
х = –7 + 20
х = 13
|
–1 – х = –20
х = –1 + 20
х = 19
|
0 – х = –20
х = 0 + 20
х = 20
|
6 – х = –20
х = 6 + 20
х = 26
|
|
24 – х = –20
х = 24 + 20
х = 44
|
–8 – х = –20
х = –8 + 20
х = 12
|
–40 – х = –20
х = –40 + 20
х = –20
|
|
Завдання 234
|
20 – (–70) = 90
|
–70 – 10 = –80
|
Завдання 235
|
а) 13 – 28 = 13 + (–28) = –15
б) 59 – (–17) = 59 + 17 = 76 |
в) –42 – 97 = (–42) + (–97) = –139 г) –89 – (–53) = (–89) + 53 = –36 |
Завдання 236
|
а) 6 – 95 = 6 – (–95) = –89 б) 24 – 96 = 24 + (–96) = –72 |
в) 33 – 67 = 33 + (–67) = –34 г) 45 – 100 = –55 |
Завдання 237
|
а) 7 – 39 = –32 |
б) 15 – 46 = –31 |
в) 28 – 82 = –54 |
г) 38 – 138 = –100 |
Завдання 238
|
а) –9 – 57 = –66 |
б) –8 – 84 = –92 |
в) –6 – 17 = –23 |
г) –1 – 297 = –298 |
Завдання 239
|
а) –17 – 53 = –70 |
б) –23 – 25 = –48 |
в) –28 – 58 = –86 |
г) –29 – 109 = –138 |
Завдання 240
|
а) 7 – (–53) = 7 + 53 = 60 б) 9 – (–28) = 9 + 28 = 37 |
в) 1 – (–77) = 1 + 77 = 78 г) 3 – (–152) = 3 + 152 = 155 |
Завдання 241
|
а) –8 – (–9) = –8 + 9 = 1 б) –7 – (–3) = –7 + 3 = –4 |
в) –5 – (–5) = –5 + 5 = 0 г) –4 – (–69) = –4 + 69 = 65 |
Завдання 242
|
а) –28 – (–7) = –28 + 7 = –21 б) 65 – (–13) = 65 + 13 = 78 |
в) –34 – 7 = –41 г) 14 – 89 = –75 |
Завдання 243
Діана в грі спочатку заробила 230 очок, а потім втратила 450 очок. Скільки очок зараз у неї на рахунку?
Розв'язання
230 – 450 = –220 (оч.) – зараз у Діани на рахунку.
Відповідь: –220 очок.
Завдання 244
Температура впала з 8 °С до –20 °С. На скільки градусів змінилася температура?
Розв'язання
–20 – 8 = –28 (°) – на стільки змінилась температура.
Відповідь: Г –28.
Завдання 245
Опівдні температура була 4 °С, а опівночі –З °С. На скільки змінилася температура повітря за пів доби?
Розв'язання
–3 – 4 = –7 (°) – на стільки змінилась температура.
Відповідь: –7°.
Завдання 246
За день температура повітря змінилася на –7 °С. Якою вона була вранці, якщо ввечері термометр показував – 2 °С?
Розв'язання
–2 – (–7) = 5 (°) – температура була зранку.
Відповідь: 5°.
Завдання 248
а) 3 – (–5) = 8 – на стільки m менше від n;
б) 7 – (–10) = 17 – на стільки m більше за n.
Завдання 249
|
а) –16 – 10 = –26 –7 – 10 = –17 0 – 10 = –10 3 – 10 = –7 9 – 10 = –1 12 – 10 = 2 |
б) –16 – (–10) = –16 + 10 = –6 –7 – (–10) = –7 + 10 = 3 0 – (–10) = 0 + 10 = 10 3 – (–10) = 3 + 10 = 13 9 – (–10) = 9 + 10 = 19 12 – (–10) = 12 + 10 = 22 |
Завдання 250
Чи правильно, що результати 209 – 45 і 45 – 209 є протилежними числами?
Розв'язання
209 – 45 = 164, 45 – 209 = –164, тому 164 і –164 є протилежними числами.
Відповідь : так.
Завдання 251
Число m протилежне числу 107. Знайди значення виразу 98 – m.
Якщо m = –107, тоді 98 – (–107) = 205
Завдання 252
Число m протилежне числу –55. Знайди значення виразу –105 – m.
Якщо m = 55, тоді –105 – 55 = –160
Завдання 253
За допомогою ресурсу змоделюй такі вирази і знайди їх значення:
|
а) 5 – 6 = –1 |
б) –2 – 3 = –5 |
в) 8 – 2 = 6 |
Завдання 254
Запиши число замість *, щоб нерівність була правильною.
|
а) 2 – 3 < 0 |
б) (–6) – (–7) > 0 |
в) –19 – (–20) < 0 |
Завдання 255
|
а) 65 – 79 = –14 |
б) –13 – 43 = –56 |
в) –124 – (–47) = –77 |
г) –390 – 63 = –453 |
Завдання 256
|
а) –12 – (–87) = 75 |
б) –63 – 29 = –92 |
в) –203 – 157 = –360 |
г) 560 – 799 = –239 |
Завдання 257
Узимку за температури повітря –23 °С в шахті вона досягає 24 °С. Знайди різницю температур.
Розв'язання
24 – (–23) = 47 (градусів) – різниця температур.
Відповідь: 47 градусів.
Завдання 258
|
а) 709 – 1000 – 34 = –325 |
б) –92 – 345 – 40 = –477 |
в) 109 – 900 – (–47) = –744 |
Завдання 259
а) (456 – 900) + (–17) = –444 + (–17) = –461
б) 56 – (0 – 345) = 56 – (–345) = 56 + 345 = 401
в) (709 – 1000) + 34 = –291 + 34 = –257
Завдання 260
а) 450 + (67 – 230) = 450 + (–163) = 450 – 163 = 287
б) (440 – 734) – 56 = (–294) – 56 = –350
в) –72 + (–45 – 234) = –72 + (–279) = –72 – 279 = –351
Завдання 261
Визнач, як розташовані точки А, В, С, К і Р:
а) відносно рівня моря;
A = 20; B = 0; C = –10; K = –25
б) відносно одна одної.
відносно B: A = 20; B = 0; C = –10; K = –25
відносно C: A = 30; B = 10; C = 0; K = –15
відносно K: A = 45; B = 25; C = 15; K = 0
Завдання 262
Пан Микола взяв іпотеку в розмірі 560 000 грн і два місяці поспіль виплачував по 24 000 грн. Скільки грошей ще має повернути пан Микола? Запиши відповідну рівність.
Розв'язання
560 000 – 24 000 – 24 000 = 512 000 (грн) – ще має повернути пан Микола.
Відповідь: 512 000 грн.
Завдання 263
Ганна хоче створити програму, що працюватиме за алгоритмом, описаним у блок–схемі. Яке вихідне значення для k отримає Ганна, якщо вхідне значення для k:
|
а) –40; –47 |
б) –4; –11 |
в) 0; –14 |
г) 34? 27 |
Завдання 264
Познач на координатній прямій точки А(–3) і В(4). Знайди відстань між точками А і В.
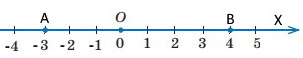
Чи правильно, що:
а) AB = |–3 – 4| = |–7| = 7; б) AB = |4 – (–3)|= |7| = 7.
Обидва варіанти правильні.
Завдання 265
Установи відповідність між значеннями k і р (1–3) та відстанню між точками К(k) і Р(р)
(А–Д).
|
1 — Г 13 2 — А 3 3 — Д 8 |
1 — k = –5 , р = 8; 8 – (–5) = 13 2 — k = –5 , р = –8; –5 – (–8) = 3 3 — k = –5 , р = 3; 3 – (–5) = 8 |
Завдання 266
|
а) –2 + x = 5 x = 5 + 2 x = 7 |
б) x – 7 = –3 x = –3 + 7 x = 4 |
в) 5 – x = 9 x = 5 – 9 x = –4 |
Завдання 267
|
а) 20 + x = 13 x = 13 – 20 x = –7 |
б) x – 17 = –23 x = –23 + 17 x = –6 |
в) 85 – x = 99 x = 85 – 99 x = –14 |
Завдання 268
Вважається, що місто Рим засноване в 753 р. до н. е. Скільки йому років тепер?
Розв'язання
2023 – (–753) = 2776 (р.) – років тепер місту Рим.
Відповідь: 2776 років.
Завдання 269
Скільки пройшло років від середини 3–го року до н. е. до середини 3–го року н. е.? Покажи на координатній прямій.

Розв'язання
3 роки до н. е. (точка А) + 3 роки н. е. (точка В) = 6 років.
Відповідь: 6 років.
Завдання 270
Відомий давньогрецький учений Арістотель народився 384 р. до н. е. У якому році відзначали його 2400–річчя?
Розв'язання
2400 – 384 = 2016 (р.) – у цьому році відзначали 2400–річчя Арістотеля.
Відповідь: 2016 р.
Завдання 271
Різницю між прибутком і видатком називають сальдо. Використовуючи дані таблиці, обчисли сальдо (в гривнях) за кожний місяць і за п'ять місяців.
|
Місяць |
Прибуток |
Видаток |
Сальдо |
|
Січень Лютий Березень Квітень Травень |
|
|
477 –940 137 –262 –162 |
|
Разом |
17865 |
19615; |
–1750 |
Завдання 272
Для яких значень a і b виконується рівність |а–b| = |a| + |b|?
a) а =–7, b = –19;
|a – b| = |–7 – (–19)| = |–7 + 19| = |12| = 12
|a| + |b| = |–7| + |–19| = 7 + 19 = 26
Рівність |a – b| = |a| + |b| не виконується.
б) а = 12, b = –17;
|a – b| = |12 – (–17)| = |12 + 17| = |29| = 29
|a| + |b| = |12| + |–17| = 12 + 17 = 29
Рівність |a – b| = |a| + |b| виконується.
в) а = 15, b = 21.
|a – b| = |15 – 21| = |–6| = 6
|a| + |b| = |15| + |21| = 15 + 21 = 36
Рівність |a – b| = |a| + |b| не виконується.
Отже, рівність |a – b| = |a| + |b| виконується тільки для варіанту б) a = 12, b = –17.
Завдання 273
Для яких значень а і b виконується рівність |а–b| = |a| – |b|?
а) a = –29, b = –6;
|a – b| = |–29 – (–6)| = |–29 + 6| = |–23| = 23
|a| – |b| = |–29| – |–6| = 29 – 6 = 23
Рівність |a – b| = |a| – |b| виконується.
б) а = –34, b = 28;
|a – b| = |–34 – 28| = |–34 – 28| = |–62| = 62
|a| – |b| = |–34| – |28| = 34 – 28 = 6
Рівність |a – b| = |a| – |b| не виконується.
в) а = –48, b = –52.
a – b| = |–48 – (–52)| = |–48 + 52| = |4| = 4
|a| – |b| = |–48| – |–52| = 48 – 52 = –4
Рівність |a – b| = |a| – |b| не виконується.
Отже, рівність |a – b| = |a| – |b| виконується для варіанту а) a = –29, b = –6.
Завдання 274
Які з чисел 5, 6, 7, 8, 9, 10 є коренями рівняння |x – 7| = |х| – 7?
Якщо х = 5, тоді |5 – 7| = |5| – 7; |–2| = 5 – 7; 2 = –2 – не є коренем;
Якщо х = 6, тоді |6 – 7| = |6| – 7; |–1| = 6 – 7; 1 = –1 – не є коренем;
Якщо х = 7, тоді |7 – 7| = |7| – 7; |0| = 7 – 7; 0 = 0 – є коренем;
Якщо х = 8, тоді |8 – 7| = |8| – 7; |1| = 8 – 7; 1 = 1 – є коренем;
Якщо х = 9, тоді |9 – 7| = |9| – 7; |2| = 9 – 7; 2 = 2 – є коренем;
Якщо х = 10, тоді |10 – 7| = |10| – 7; |3| = 10 – 7; 3 = 3 – є коренем.
Рівняння |х – 7| = |х| – 7 має корені при х = 7, 8, 9, 10
Завдання 275
Які з чисел–5, –4, –3, –2, –1 є коренями рівняння |х + 3| = х + 3?
|–5 + 3| = –5 + 3; |–2| = –2; 2 = –2 – не є коренем;
|–4 + 3| = –4 + 3; |–1| = –1; 1 = –1 – не є коренем;
|–3 + 3| = –3 + 3; |0| = 0; 0 = 0 – є коренем;
|–2 + 3| = –2 + 3; |1| = 1; 1 = 1 – є коренем;
|–1 + 3| = –1 + 3; |2| = 2; 2 = 2 – є коренем.
Рівняння |х + 3| = х + 3 має корені при х = –3, –2, –1
Завдання 276
|
а) |3 + х| = 5 |
б) |х – 8| = 2 |
||
|
3 + х = 5 або 3 + x x = 5 – 3 x = 2 |
3 + x = –5 x = –5 – 3 x = –8 |
x – 8 = 2 або x = 2 + 8 x = 10 |
x – 8 = –2 x = –2 + 8 x = 6 |
|
в) 6 + |4 – х| = 9 |
г) |х + 5| – 5 = 4 | ||
|
|4 – x| = 9 – 6 або 4 – x = 3 x = 4 – 3 x = 1 |
4 – x = –3 x = 4 – (–3) x = 7 |
|x + 5| = 4 + 5 або x + 5 = 9 x = 9 – 5 x = 4 |
x + 5 = –9 x = –9 – 5 x = –14 |
Завдання 277
|
а) |7 + х| = 9 |
б) |х – 6| = 8 |
||
|
|7 + х| = 9 або 7 + x = 9 x = 9 – 7 x = 2 |
7 + x = –9; x = –9 – 7; x = –16 |
|х – 6| = 8 або x – 6 = 8 x = 8 + 6 x = 14 |
x – 6 = –8 x = –8 + 6 x = –2 |
|
в) |х – 2| + 3 = 6 |
г) |х + 12| – 5 = 9 | ||
|
|x – 2| = 6 – 3 або |x – 2| = 3 x – 2 = 3 x = 3 + 2 x = 5 |
x – 2 = –3 x = –3 + 2 x = –1 |
|x + 12| = 9 + 5 або |x + 12| = 14 x + 12 = 14 x = 14 – 12 x = 2 |
x + 12 = –14 x = –14 – 12 x = –26 |
Завдання 278
Порівняй значення виразів А і В, якщо:
а) A = 36 + (–28) – 32 + (–16);
В = (–36 + 28 – (–16)) – (36 – (–12) – 50).
A = 36 + (–28) – 32 + (–16) = 36 – 28 – 32 – 16 = –40
B = (–36 + 28 – (–16)) – (36 – (–12) – 50) = 8 – (–2) = 10
A < B на 50 одиниць.
б) А = –72 + (–28) – (–46) + 34 + (–18);
В = (128 – 302) – (–36) – (–64 – (–102)).
A = –72 + (–28) – (–46) + 34 + (–18) = –72 – 28 + 46 + 34 – 18 = –38
B = (128 – 302) – (–36) – (–64 – (–102)) = –138 – 38 = –176
A > B на 138 одиниць.
Завдання 279 Рівняння
|
а) х² = 64 х = 8 або х = –8 |
б) (х – 2)² = 25 (х – 2)² = 5² x – 2 = 5 або x – 2 = –5 x = 5 + 2 або х = –5 + 2 x = 7 або х = –3 |
Завдання 280
Кожне просте число має тільки два дільники. А які числа мають тільки по три дільники?
Числа, які є квадратами простих чисел, тобто числа вигляду р², де р — просте число, дільниками якого є числа 1, р, р².
Завдання 281
На малюнку показано орієнтовний розподіл часових зон на планеті. Котра година у виділених містах, якщо:
а) у Грінвічі 0:00;
у Києві — 2:00; у Нью–Йорку — 19:00; у Варшаві — 1:00; у Токіо — 9:00
б) у Грінвічі 06:00;
у Києві — 8:00; у Нью–Йорку — 1:00; у Варшаві — 7:00; у Токіо — 15:00
в) у Грінвічі 20:00;
у Києві — 22:00; у Нью–Йорку — 15:00; у Варшаві — 21:00; у Токіо — 5:00
г) у Києві 10:00;
у Грінвічі — 8:00; у Нью–Йорку — 3:00; у Варшаві — 9:00; у Токіо — 17:00
ґ) у Києві 16:00.
у Грінвічі — 14:00; у Нью–Йорку — 9:00; у Варшаві — 15:00; у Токіо — 23:00
Вправи для повторення
Завдання 282
Знайди число, 7,5 % якого становлять:
а) 27; (27 • 100) : 7,5 = 0,075 • 27 = 360
б) 34,8; (34,8 • 100) : 7,5 = 0,075 • 34,8 = 464
в) 7,5. (7,5 • 100) : 7,5 = 0,075 • 7,5 = 100
Завдання 283
Петрик і Галинка зібрали разом 12,4 кг суниць. Скільки суниць зібрав Петрик, якщо Галинка зібрала на 2 кг більше?
Розв'язання
Нехай Петрик зібрав х кг суниць, тоді Галинка зібрала (х + 2) кг суниць. Складаємо рівняння.
x + x + 2 = 12,4
2x = 12,4 – 2
2x = 10,4
x = 5,2 (кг) – зібрав Петрик суниць.
Відповідь: 5,2 кг.
Завдання 284
Від поля, площа якого дорівнює 12 га, відокремили ділянку у формі прямокутника, розміри якого 60 м і 50 м. Знайди площу ділянки, яка залишилася.
Розв'язання
1) 60 • 50 = 3 000 (м²) = 0,3 (га) – площа відокремленої ділянки;
2) 12 – 0,3 = 11,7 (га) – площа ділянки, яка залишилась.
Відповідь: 11,7 га.