Завдання 1351
Приклади перпендикулярних прямих на предметіах довкілля: кути стола, кути будівель, сітка на тенісному столі, перехрестя дороги.
Приклади паралельних прямих на предметах довкілля: лінії електропередачі, книжкові поличи, дороги, рейки на залізничних коліях, паркан.
Завдання 1352
|
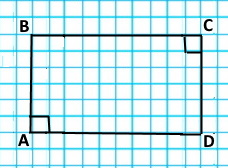
а) Перпендикулярні прямі: b ⊥ d
Паралельні прямі: відсутні
|
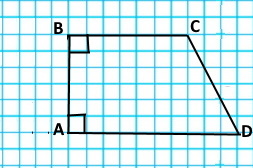
б) Перпенликулярні прямі: a ⊥ d, c ⊥ d
Паралельні прямі: а ∥ с
|
Завдання 1353
1) NK ∥ ML, KL ∥ NM
NK ⊥ KL, KL ⊥ LM, LM ⊥ MN, MN ⊥ NK
2) Прямі PL і NM не є паралельними.
Завдання 1354
Паралельні прямі: a ∥ l, b ∥ c
Завдання 1355
Перпендикулярні прямі: a ⊥ m, b ⊥ l, b ⊥ c
Завдання 1356
Накресліть деякий квадрат ABCD і проведіть прямі AC та BD.

AC ⊥ BD
Завдання 1357, 1358
|
Через точку О провели пряму, перпендикулярну до прямої m, та пряму, паралельну прямій n.
 |
Через точку С провели пряму, перпендикулярну до прямої а, та пряму, паралельну прямій b.
 |
Завдання 1359
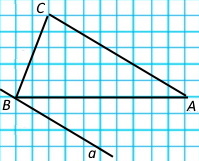
Накресліть деякий трикутник АВС і через точку В проведіть:
|
1) пряму, перпендикулярну до прямої АВ
 |
2) пряму, паралельну прямій АС
 |
Завдання 1360
Накресліть пряму b і позначте точку K, що не належить цій прямій. Через K проведіть:
|
1) пряму c, перпендикулярну до прямої b;
 |
2) пряму d, паралельну прямій b.
 |
Завдання 1361
Накресліть деяку пряму а. Проведіть дві прямі b і с, паралельні прямій а. Користуючись лінійкою та косинцем, переконайтеся, що b || с.
Одну сторону прямого кута косинця прикладаємо до прямої b. До іншої сторони прямого кута косинця прикладаємо лінійку і пересуваємо вздовж неї косинець, поки перша сторона прямого кута не опиниться на прямій с. Прямі b i c дійсно паралельні.

Завдання 1362
Накресліть деякі дві перпендикулярні прямі а і b та позначте поза ними деяку точку М. Проведіть через цю точку пряму с, перпендикулярну до прямої а, і пряму d, перпендикулярну до прямої b.
Паралельні прямі: a ∥ d, b ∥ c

Завдання1363
Накресліть деякий трикутник АВС. Виміряйте довжину сторони АВ та позначте її середину буквою D. Через точку D проведіть пряму, паралельну прямій АС. Переконайтеся, що проведена пряма ділить сторону ВС навпіл. За допомогою лінійки переконуємося, що відрізки BE і ЕС рівні.

Завдання 1364
Накресліть деякий тупокутний трикутник KLM. Через кожну вершину трикутника проведіть пряму, паралельну протилежній стороні.

Завдання 1365
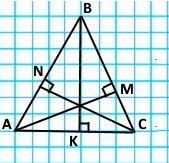
Накресліть деякий гострокутний трикутник АВС. Через кожну вершину трикутника проведіть пряму, перпендикулярну до протилежної сторони.
Завдання 1366
Накресліть чотирикутник АВСD, у якого:
|
1) сторони АВ і СD перпендикулярні до сторони АD;
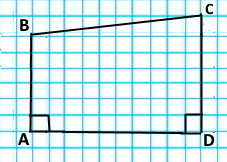 |
2) протилежні сторони паралельні.
|
Завдання 1367
Накресліть чотирикутник, у якого:
|
1) дві сусідні сторони перпендикулярні;
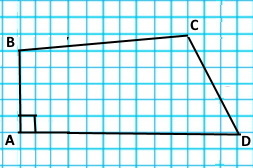 |
2) дві протилежні сторони паралельні, а дві — не паралельні.
|
Завдання 1368
На рисунку 135 кут LОА становить третину прямого кута. Знайдіть величини кутів LОА, LОС, LОD та LОВ.
Розв'язання
1) 90° : 3 = 30° – ∠LOA;
2) 90° – 30° = 60° – ∠LOC;
3) 90° + 30° = 120° – ∠LOD;
4) 90° + 60° = 150° – ∠LOB.
Відповідь:30°; 60°; 120°; 150°.
Завдання 1369
На рисунку 136 промінь ОK ділить кут СОВ навпіл. Знайдіть величини кутів KОВ, DОK та АОK.
Розв'язання
1) 90° : 2 = 45° – ∠KOB;
2) 90° + 45° = 135 ° – ∠DOK або ∠AOK.
Відповдіь: 45°; 135°; 135°.
Завдання 1370
На рисунку 137 АВ ⊥ СD, MN ⊥ KL, кут АОK на 28° більший за кут KОС. Знайдіть величини кутів АОK, KОС, KОВ.
Розв'язання
Нехай ∠КОС = х градусів, тоді ∠АОК = х + 28 градусів. Складаємо рівняння:
х + х + 28° = 90°
2х = 62°
х = 31° – ∠КОС;
31° + 28° = 59° – ∠АОК;
90° + 31° = 121° – ∠КОВ.
Відповідь: 31°; 59°; 121°.
Завдання 1371
На рисунку 137 АВ ⊥ СD, MN ⊥ KL, кут KОС удвічі менший від кута АОK. Знайдіть величини кутів KОС, СОN, МОС.
Розв'язання
Нехай ∠КОС = х градусів, тоді ∠АОК = 2х градусів. Складаємо рівняння:
х + 2х = 90°
3х = 90°
х = 30° – ∠КОС;
90° – 30° = 60° – ∠CON;
90° + 30° = 120° – ∠MOC.
Відповідь: 30°; 60°; 120°.
Завдання 1372
У школі є три шості класи. У 6-А класі навчається найбільше дітей, а в 6-Б і 6-В разом — 55 дітей. Скільки щонайменше дітей може навчатися в цих класах разом?
Розв'язання
1) 55 : 2 = 27 (ост.1). Отже в 6-Б може навчатися 27 д., в 6-В — 28 д., а 6-А класі — 29 д.
2) 55 + 29 = 84 (д.) – в цих класах разом.
Відповдіь: 84 дитини.
Вправи для повторення
Завдання 1373
Координати точок: В(–6) і С(2).

Завдання 1374
Ділянка прямокутної форми завдовжки 60 м має площу 750 м². Знайдіть периметр ділянки.
Розв'язання
1) 750 : 60 = 12,5 (м) – ширина ділянки;
2) (60 + 12,5) • 2 = 145 (м) – периметр ділянки.
Відповідь: 145 м.
Завдання 1375
Середнє арифметичне двох чисел дорівнює 4,2. Одне з них утричі більше за друге. Знайдіть ці числа.
Розв'язання
Нехай друге число х, тоді перше — 3х. Складаємо рівняння:
(х + 3х) : 2 = 4,2
4х = 8,4
х = 8,4 : 4
х = 2,1 – друге число;
3 • 2,1 = 6,3 – перше число.
Відповідь: 6,3; 2,1.
Завдання 1376
Задача-жарт. Два жуки змагаються з бігу на 50 м. Перший жук пробігає 1 м за 5 с, а другий — за 4,6 с. Після подолання кожних 10 м дистанції жуки зупиняються на перепочинок: перший — на 10 с, а другий — на 15 с. Який жук фінішує першим? Чи зміниться відповідь, якщо довжина дистанції дорівнює 100 м? 30 м?
Розв'язання
1) 5 • 50 + 10 • 4 = 290 (с) – загальний час першого на дистанції 50 м;
2) 4,6 • 50 + 15 • 4 = 290 (с) – загальний час другого на дистанції 50 м;
2) 4,6 • 50 + 15 • 4 = 290 (с) – загальний час другого на дистанції 50 м;
3) 5 • 100 + 10 • 9 = 590 (с) – загальний час першого на дистанції 100 м;
4) 4,6 • 100 + 15 • 9 = 595 (с) – загальний час другого на дистанції 100 м;
4) 4,6 • 100 + 15 • 9 = 595 (с) – загальний час другого на дистанції 100 м;
5) 5 • 30 + 10 • 2 = 170 (с) – загальний час першого на дистанції 30 м;
6) 4,6 • 30 + 15 • 2 = 168 (с) – загальний час другого на дистанції 30 м.
6) 4,6 • 30 + 15 • 2 = 168 (с) – загальний час другого на дистанції 30 м.
Відповідь: фінішують одночасно. Якщо довжина дистанції дорівнюватиме 100 м, то переможе перший жук, якщо 30 м — другий.