Завдання 1461 Відношення

Із 6 га поля зібрали 108 ц гречки. Скільки центнерів гречки зберуть із 15 га цього поля, якщо врожайність на всіх його ділянках однакова?

Розв'язання

6 га — 108 ц

15 га — х ц

6/15 = 108/х; х = 108 • 15 : 6; х = 270 (ц)

Відповідь: зберуть 270 ц гречки.

 

Завдання 1466

На принтері мають надрукувати 90 сторінок тексту. Перші 18 сторінок принтер надрукував за 1,2 хв. За скільки хвилин принтер надрукує решту сторінок?

Розв'язання

18 с. — 1,2 хв

72 с. — х хв

1) 90 – 18 = 72 (с.) – решта сторінок;

18/72 = 1,2/х; х = 72 • 1,2 : 18; х = 4,8 (хв)

Відповідь: прінтер надрукує решту сторінок за 4,8 хв.

 

Завдання 1467

2,5 кг сплаву олова, міді й цинку містять 800 г олова та 900 г міді. Скільки грамів олова і скільки грамів цинку міститься в 3,5 кг такого сплаву?

Розв'язання

800 г = 0,8 кг; 900 г = 0,9 кг

1 спосіб

1) 2,5 – (0,8 + 0,9) = 0,8 (кг) – цинку в сплаві;

2) 0,8 : 2,5 • 100% =  32% – складає цинк або олово в сплаві;

3) 3,5 • 0,32 = 1,12 (кг) = 1120 (г) – цинку або олова в сплаві.

2 спосіб

1) 2,5 – (0,8 + 0,9) = 0,8 (кг) – цинку в сплаві;

2) 2,5 кг — 0,8 кг

    3,5 кг — х кг

2,5/3,5 = 0,8/х; х = 0,8 • 3,5 : 2,5; х = 1,12 (кг) = 1120 г

Відповідь: олова і цинку в сплаві по 1120 г.

 

Завдання 1468

Басейн наповнили водою за 8 год, подаючи щогодини по 175 м3 води. За скільки годин наповнився б басейн, якби щогодини в нього поступало по 200 м3 води?

Розв'язання

175 м³ — 8 год

200 м₃ — х год

175/200 = х/8; х = 175 • 8 : 200; х = 7 (год)

Відповідь: басейн наповнився б за 7 год.

 

Завдання 1469

Периметр ділянки прямокутної форми дорівнює 28 м. Знайдіть сторони ділянки, якщо вони відносяться як 4 : 3.

Розв'язання

1 спосіб

Нехай коефіцієнт пропорційності х, тоді перша сторона має довжину 4х м, а друга — 3х м. Складаємо рівняння:

(4х + 3х) • 2 = 28

5х • 2 = 28

10х = 20

х = 20 : 10

х = 2

4 • 2 = 8 (м) – перша сторона прямокутника;

3 • 2 = 6 (м) – друга сторона прямокутника.

2 спосіб

1) 28 : 2 = 14 (м) – сума двох сторін;

2) 4 + 3 = 7 (ч.) – всього частин;

3) 14 : 7 = 2 (м) – припадає на 1 частину;

4) 4 • 2 = 8 (м) – перша сторона прямокутника;

5) 3 • 2 = 6 (м) – друга сторона прямокутника.

Відповідь: 8 м; 6 м.

 

Завдання 1470

У саду ростуть яблуні, груші та сливи, кількості яких відносяться як 6 : 2 : 3. Скільки всього дерев у саду, якщо в ньому: 1) 9 слив; 2) груш на 8 менше, ніж яблунь?

Розв'язання

1) 9 слив;

1 спосіб

Нехай коефіцієнт пропорційності х, тоді яблунь в саду 6х дерев, груш — 2х дерев, а слив — 3х дерев. Складаємо рівняння:

3х = 9

х = 3

3 • 11 = 33 (д.) – дерев в саду.

2 спосіб

1) 9 : 3 = 3 (д.) – складає 1 частина;

2) 6 + 2 + 3 = 11 (ч.) – всього частин;

3) 3 • 11 = 33 (д.) – дерев в саду.

Відповідь: 33 дерева.

2) груш на 8 менше, ніж яблунь?

1 спосіб

Нехай коефіцієнт пропорційності х, тоді яблунь в саду 6х дерев, груш — 2х дерев, а слив — 3х дерев. Складаємо рівняння:

6х – 2х = 8

4х = 8

х = 8 : 4

х = 2

2 • 11 = 22 (д.) – дерев в саду.

2 спосіб

1) 6 – 2 = 4 (ч.) – на стільки менше частин;

2) 8 : 4 = 2 (д.) – припадає на 1 частину;

3) 6 + 2 + 3 = 11 (ч.) – всього частин;

4) 2 • 11 = 22 (д.) – дерев в саду.

Відповідь: 22 дерева.

 

Завдання 1471

Відстань між Києвом і Черкасами 420 км. Знайдіть відстань між цими містами на карті з масштабом 1 : 5 000 000.

Розв'язання

50 км — 1 см

420 км — х см

50/420 = 1/х; х = 420 • 1 : 50; х = 8,4 (см)

Відповідь: на карті відстань між містами 8,4 см.

 

Завдання 1472

Автомобіль проїхав шлях, якому на карті з масштабом 1 : 8 000 000 відповідає відстань 2,7 см. З якою швидкістю рухався автомобіль, якщо поїздка тривала 3 год?

Розв'язання

1 см — 80 км

2,7 см — х км

1/2,7 = 80/х; х = 80 • 2,7 : 1; х = 216 (км)

216 : 3 = 72 (км/год)

Відповідь: автомобіль рухався зі швидкістю 72 км/год.

 

Завдання 1473

У трьох будинках разом 630 мешканців. У першому будинку 250 мешканців, у другому — 80 % тієї кількості, що в першому. Скільки мешканців у третьому будинку?

Розв'язання

1) 250 • 0,8 = 200 (м.) – у другому будинку;

2) 630 – (250 + 200) = 630 – 450 = 180 (м.)

Відповідь: у третьому будинку 180 мешканцв.

 

Завдання 1474

Сплав міді й олова містить 75 % міді. Скільки грамів міді містить сплав, якщо в ньому є 120 г олова?

Розв'язання

1 спосіб

1) 100% – 75% = 25% – олова в сплаві;

2) 120 : 25 • 100 = 480 (г) – маса сплава;

3) 480 – 120 = 360 (г) – маса міді в сплаві.

2 спосіб

1) 100% – 75% = 25% – олова в сплаві;

2) 120 г — 25%

    х г — 100%

120/х = 25/100; х = 120 • 100 : 25; х = 480 (г) – маса сплаву.

3) 480 – 120 = 360 (г)

Відповідь: сплав містить 360 г міді.

 

Завдання 1475

Три автомати розфасували цукор. Перший автомат розфасував 30 % усього цукру, другий — в 1,2 раза більше, ніж перший, а третій — 340 кг. Скільки всього кілограмів цукру розфасували автомати?

Розв'язання

Нехай було х кг цукру, тоді перший розфасує 0,3х кг, а другий — 0,3х • 1,2 = 0,36х кг. Складаємо рівняння.

0,3х + 0,3х • 1,2 + 340 = х

0,3х + 0,36х – х = –340

–0,34х = –340

х = 1000

Відповідь: автомати розфасували 1000 кг цукру.

 

Завдання 1476

Фірма отримала 60 000 грн прибутку, з яких 24 000 грн витратила на розширення виробництва. Скільки відсотків отриманого прибутку фірма витратила на розширення виробництва?

Розв'язання

24000 : 60000 • 100% = 0,4 • 100% = 40%

Відповідь: на розширення виробництва фірма витратила 40% отриманого прибутку.

 

Завдання 1477

Довжина поля дорівнює 100 м, а ширина — 40 м. 1) На скільки відсотків ширина поля менша від довжини? 2) На скільки відсотків довжина поля більша за ширину?

Розв'язання

1 спосіб

1) 100 – 40 = 60 (м)  – на стільки менша ширина поля;

2) 60 : 100 • 100% = 60% – на стільки відсотків менша ширина поля від довжини;

3) 100 – 40 = 60 (м)  – на стільки більша довжина поля;

4) 60 : 40 • 100% = 150% – на стільки відсотків більша довжина поля від ширини.

2 спосіб

1) 100 м — 100%

    40 м — х%

100/40 = 100/х; х = 40 • 100 : 100; х = 40 (%)

100% – 40% = 60%

2) 40 м — 100%

    100 м — х%

40/100 = 100/х; х = 100 • 100 : 40; х = 250 (%)

250% – 100% = 150%

Відповідь: 1) 60%; 2) 150%.

 

Завдання 1478

Товар коштував 1000 грн. Спочатку цю ціну збільшили на 5 %, а згодом нову ціну зменшили на 10 %. Знайдіть ціну товару після двох переоцінок.

Розв'язання

1 спосіб

1) 1000 + 1000 • 0,05 = 1050 (грн) – ціна після першої переоцінки;

2) 1050 – 1050 • 0,1 = 945 (грн) – ціна після двох переоцінок.

2 спосіб

1000 грн — 100%

х грн — 105%

1000/х = 100/105; х = 1000 • 105 : 100; х = 1050 (грн) – ціна після першої переоцінки;

1050 грн — 100%

х грн — 90%

1050/х = 100/90; х = 1050 • 90 : 100; х = 945 (грн) – ціна після двох переоцінок.

Відповідь: 945 грн.

 

Завдання 1479

Сплав міді та цинку, загальна маса якого 2 кг, містить 75 % міді. Скільки грамів цинку потрібно додати до цього сплаву, щоб одержати новий сплав, який містив би 60 % міді?

Розв'язання

1 спосіб

1) 2 • 0,75 = 1,5 (кг) – міді в початковому сплаві;

2) 1,5 : 0,6 = 2,5 (кг) – маса нового сплаву;

3) 2,5 – 2 = 0,5 (кг) = 500 (г) – цинку потрібно додати.

2 спосіб

1) 2 кг — 100%

   х кг — 75%

2/х = 100/75; х = 75 • 2 : 100; х = 1,5 (кг) – міді в початковому сплаві;

2) 1,5 кг — 60%

    х кг — 100%

1,5/х = 60/100; х = 1,5 • 100 : 60; х = 2,5 (кг) – маса нового сплаву;

3) 2,5 – 2 = 0,5 (кг) = 500 (г) – цинку потрібно додати.

Відповідь: 500 г.

 

Завдання 1480

Накресліть коло, радіус якого дорівнює 15 мм, та знайдіть його довжину.

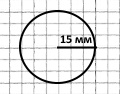
Розв'язання

2 • 3,14 • 15 = 94,2 (мм) = 9,42 (см)

Відповідь: довжина кола 9,42 см.

 

Завдання 1481

Знайдіть площу круга, діаметр якого дорівнює 6 см; 18 мм.

Розв'язання

1) 6 : 2 = 3 (см) – радіус круга з діаметром 6 см;

2) 3,14 • 3² = 28,26 (см²) – площа круга з діаметром 6 см;

3) 18 : 2 = 9 (мм) – радіус круга з діаметром 18 мм;

4) 3,14 • 9² = 254,34 (мм²) – площа круга з діаметром 18 мм.

Відповідь: 28,26 см²; 254,34 мм².

 

Завдання 1482

Довжина кола дорівнює 18,84 см. Знайдіть площу круга, радіус якого вдвічі більший за радіус даного кола.

Розв'язання

l = 2пr; s = п•r²

1) 18,84 : (2 • 3,14) = 18,84 : 6,28 = 3 (см) – радіус кола;

2) 3 • 2 = 6 (см) – радіус нового кола;

3) 3,14 • 6² = 113,04 (см²) – площа круга.

Відповідь: 113,04 см².

 

Завдання 1483

Знайдіть площу фігури, якщо сторона кожного квадрата дорівнює 1 см.

Розв'язання

1) 3,14 • 4² = 50,24 (см²) – площа великого круга;

2) 3,14 • 2² • 2 = 25,12 (см²) – площа двох малих кругів;

3) 50,24 – 25,12 = 25,12 (см²) – площа фігури.

Відповідь: 25,12 см².

 

Завдання 1484

У магазин привезли 120 кг фруктів: яблука, банани, сливи й абрикоси. На рисунку 163 зображено діаграму розподілу мас цих фруктів. 1) Скільки відсотків маси всіх фруктів становить маса слив? 2) Фруктів якого виду привезли найбільше? Найменше? 3) Скільки кілограмів фруктів кожного виду привезли в магазин?

Короткий запис

15 % — абрикоси

40 % — яблука

25 % — банани

х% — сливи

Розв'язання

1) 100% – (15% + 40% + 25%) = 20% – складають сливи;

2) 120 • 0,15 = 18 (кг) – привезли абрикосів;

3) 120 • 0,4 = 48 (кг) – привезли яблук;

4) 120 • 0,25 = 30 (кг) – привезли бананів;

5) 120 • 0,2 = 24 (кг) – привезли слив.

Відповідь: 1) 20%; 2) найбільше — яблук, найменше — абрикосів; 3) 18 кг абрикосів, 48 кг яблук, 30 кг бананів, 24 кг слив.

 

Завдання 1485

Паперова смужка охоплює бічну поверхню банки циліндричної форми. Знайдіть площу смужки, якщо радіус банки дорівнює 4 см, а висота — 20 см.

Розв'язання

1) 2 • 3,14 • 4 = 25,12 (см) – ширина смужки;

2) 25,12 • 20 = 502,4 (см²) – площа смужки.

Відповідь: 502,4 см².

Інші завдання дивись тут...