Завдання 1408

Воду в посудині почали нагрівати. На рисунку 152 зображено графік зміни температури води протягом 16 хвилин.

1) Початкова температура води 20°С, кінцева температура 80°С.

2) Найменша температура води 20°С. Найбільша температура води 100°С;

3) Якщо t = 4, тоді Т = 60°С;

   якщо t = 5, тоді Т = 70°С;

   якщо t = 10,тоді Т = 100°С;

4) Якщо Т = 40, тоді t = 2 хв;

   якщо Т = 50, тоді t = 3 хв;

5) Температура води підвищувалася протягом 8 хв.

   Знижувалася протягом 16 хв – 10 хв = 6 хв.

   Не змінювалася протягом 10 хв – 8 хв = 2 хв.

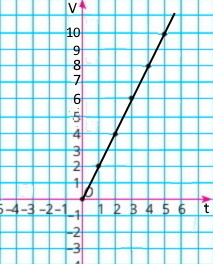
На рисунку 153 зображено графік зміни об’єму води в баку залежно від часу. На осі абсцис відкладено значення часу t (у хвилинах), а на осі ординат — значення об’єму V (у літрах). Користуючись графіком, знайдіть:

1) початковий об’єм води в баку 40 л;

2) Якщо t = 2, тоді об’єм води V = 30 л;

   якщо t = 5, тоді V = 15 л;

3) Якщо V = 20, тоді значення часу t = 4 хв;

   якщо V = 35, тоді  t = 1 хв.

Велосипедистка їде зі швидкістю 20 км/год. На рисунку 154 зображено графік залежності шляху s (у км), який проїхала велосипедистка, від часу руху t (у год). Користуючись графіком, знайдіть:

1) Якщо t = 2, тоді велосипедистка проїхала шлях S = 40 км;

   якщо t = 2,5, тоді велосипедистка проїхала шлях S = 50 км;

2) якщо s = 60, тоді час руху t = 3 год;

   якщо s = 30, тоді t = 1,5 год;

3) увесь шлях велосипедистки S = 80 км.

t, год	0	1	2	3	4	5	6	7	8	9	10
Т, °С	2	3	0	2	–1	–2	1	0	1	1	3

Завдання 1413

Автомобіль здійснив поїздку від Хмельницького до Києва. На рисунку 155 зображено графік зміни відстані s від автомобіля до Києва залежно від часу руху t.

1) Поїздка тривала 4,5 год;

2) Якщо t = 2,5, тоді S = 160 км;

   якщо t = 4, тоді S = 40 км;

3) На відстані 240 км від Києва автомобіль перебував t = 1 год . На відстані 40 км

t = 4 год;

4) Автомобіль під час поїздки зупинявся. Тривалість зупинки 2,5 год – 2 год = 0,5 год;

5) Протягом перших двох годин автомобіль рухався зі швидкістю:

(320 км – 160 км) : 2 год = 80 км/год.

Автобус здійснив поїздку від міста А до міста С, зробивши зупинку в місті В. На рисунку 156 зображено графік залежності шляху s (у км), який проїхав автобус, від часу руху t (у год).

1) Поїздка тривала 5 год;

2) Автобус проїхав 280 км;

3) Якщо t = 2, тоді автобус проїхав S = 140 км;

   якщо t = 3, тоді S = 140 км;

   якщо t = 4, тоді S = 210 км;

4) Автобус перебував у місті В 3 год – 2 год = 1 год

5) Протягом перших двох годин руху автобус їхав зі швидкістю;

140 км : 2 год = 70 км/год.

1) Через 1 год руху туристи перебували на відстані S = 4 км; через 5 год – S = 12 км;

2) Кінцевий пункт розташований від табору на відстані S = 8 км;

3) До першої зупинки туристи рухалися t = 1,5 год; До кінцевого пункту – t = 6 год;

4) Туристи відпочивали (2 год – 1,5 год) + (5 год – 4 год) = 0,5 год + 1 год = 1,5 год;

5) Туристи вирушили назад через 6 год;

6) Протягом перших 1,5 год руху туристи йшли зі швидкістю 6 км : 1,5 год = 4 км/год;

   Від другої до четвертої години руху:

   (12 км – 6 км ) : (4 год – 2 год) =  6 км : 2 год = 3 км/год;

   Від п’ятої до шостої години руху:

   (12 км – 8 км) : (5 год – 6 год) = 4 км : 1 год = 4 км/год.

На столі вряд стоять 4 тарілки. Чи можна на ці тарілки розкласти 25 яблук так, щоб кількості яблук на сусідніх тарілках відрізнялися на 1?

Ні, не можна, бо  25 : 4 = 5 (ост. 5), а 5 = 1 + 2 + 2.

1) –2 3/8 + 2 • (1 1/2 – 5/8) = –2 3/8 + (3 – 5/4) = –2 3/8 + 1 6/8 = –5/8

2) (3 2/9 – 12 2/3  + 1 1/6) : 1/36 = (3 4/18 – 12 12/18  + 1 3/18) : 1/36 = –8 5/18 : 1/36 =

= –149/18 • 36/1 = –149 • 3 = –298

1) (–5,6 + a) – (a – 0,8) = –5,6 + a – a + 0,8 = –4,8

2) (14 – b) – (b – (21 – b)) = (14 – b) – (b – 21 + b) = 14 – b – b + 21 – b = 35 – 3b

Завдання 1424

Промінь ділить розгорнутий кут на два кути, величина одного з яких становить 125 % від величини другого. Знайдіть величину кожного з утворених кутів.

Розв'язання

Нехай другий кут дорівнює х, тоді перший — 1,25х. Складаємо рівняння:

х + 1,25х = 180

2,25х = 180

х = 180 : 2,25

х = 80 – другий кут;

1,25 • 80 = 100 – перший кут.

Відповідь: 100°; 80°.

Завдання 1425

Із Вінниці до Львова виїхала вантажівка, а через годину вслід за нею — легковий автомобіль. На якій відстані від Вінниці легковий автомобіль наздожене вантажівку, якщо його швидкість дорівнює 100 км/год, а вантажівки — 75 км/год?

Розв'язання

Нехай автомобіль проїхав х год, тоді вантажівка (х + 1) год. Складаємо рівняння:

100х = 75(х + 1)

100х – 75х = 75

25х = 75

х = 3

100 • 3 = 300 (км)

Відповдіь: за 300 км від Вінниці автомобіль наздожене вантажівку.

Інші завдання дивись тут...