Накресліть коло з центром O і радіусом 3 см. Проведіть пряму через точку O і позначте точки її перетину з колом буквами A і B.
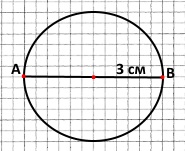
1) Відрізки OA і OB — радіуси.
2) OA = 3 см.
3) Відрізок AB називається діаметром.
4) AB = 6 см.
Завдання 691
Укажіть радіус, хорду та діаметр кола із центром B, зображеного на рисунку 35. Скільки радіусів і скільки хорд зображено на цьому рисунку?
BA, BK, BM — радіуси; МР — хорда; МК — діаметр. Усього 3 радіусів і 1 хорда.
Завдання 692
1) лежать на колі точки: D, M, C
2) належать кругу точки: D, M, C, B, K, O, F
3) не лежать на колі точки: E, P, B, K, O, F, A
4) не належать кругу точки: E, P, A
Завдання 693
1) Кругу належать точки: E, D, F, O, M, N і належить точка P
2) Радіуси круга: OD, ОЕ, OM, ON
3) OF < r < OP, де r — радіус кола.
Завдання 694
На око : r1 < r2. Перевірили вимірюванням: радіуси кіл однакові.
Завдання 695
Знайдіть діаметр кола, радіус якого дорівнює:
1) 14 см; 2 • 14 = 28 (cм) - діаметр кола;
2) 4 см 5 мм; 2 • 4 см 5 мм = 9 (cм) - діаметр кола;
3) 3,6 дм. 2 • 3,6 дм = 7,2 (дм) - діаметр кола.
Завдання 696
Знайдіть радіус кола, діаметр якого дорівнює:
1) 8 см; 8 : 2 = 4 (см) - радіус кола;
2) 5 см; 5 : 2 = 2,5 (см) - радіус кола;
3) 9,2 дм. 9,2 : 2 = 4,6 (см) - радіус кола.
Завдання 697
Накресліть коло радіуса 2 см 5 мм із центром M. Обчисліть діаметр цього кола.
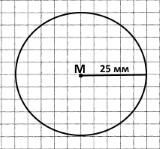
2 см 5 мм • 2 = 4 см 10 мм = 5 см — діаметр кола.
Завдання 698
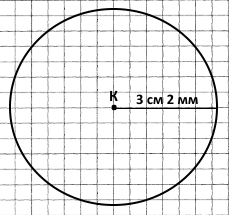
Накресліть коло радіуса 3 см 2 мм із центром K. Обчисліть діаметр цього кола.
3 см 2 мм • 2 = 6 см 4 мм — діаметр кола.
Завдання 699
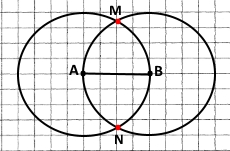
Позначте дві довільні точки A і B, виміряйте відстань між ними. Побудуйте коло із центром A, яке проходить через точку B, і коло із центром B, яке проходить через точку A. Чому дорівнює радіус кожного з побудованих кіл? Позначте точки перетину кіл. Яка відстань від цих точок до центрів кіл?
Радіуси кіл дорівнюють відстані між точками А і В.
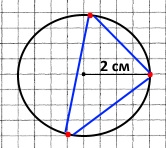
АМ = AN = BN = BM = AB = 2 см
Завдання 700
Накресліть відрізок AB завдовжки 5 см. Побудуйте коло радіуса 3 см із центром A та коло радіуса 4 см із центром B.
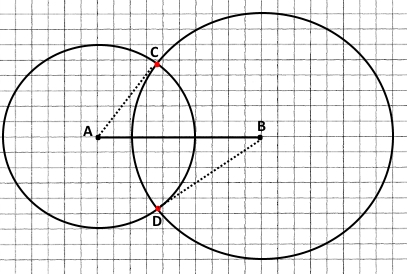
Існує дві точки перетину кіл.
Відстань від кожної з цих точок до точки A дорівнює радіусу кола з точкою А, тобто 3 см.
Відстань від кожної з цих точок до точки В дорівнює радіусу кола з точкою В, тобто 4 см.
Завдання 701
Накресліть довільний відрізок AB. Побудуйте коло так, щоб цей відрізок був його діаметром.

Завдання 702
Знайдіть периметр чотирикутника O1AO2B, якщо радіуси кіл дорівнюють 5 см і 3 см.
Р = 5 см + 8 см + 8 см + 5 см = 26 см
Завдання 703
Накресліть три кола, які мають спільний центр і радіуси яких відповідно дорівнюють 2 см, 3 см і 4 см.
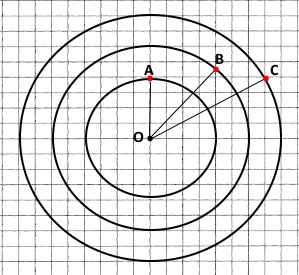
ОА = 2 см; ОВ = 3 см; ОС = 4 см.
Завдання 704
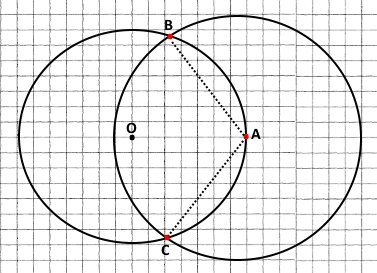
Накресліть коло, діаметр якого дорівнює 7 см. Позначте на колі точку A. Знайдіть на колі точки, віддалені від точки A на 4 см.
Проводимо коло з центром в точці А і з радіусом 4 см. У перетині з колом із радіусом ОА = 3,5 см отримаємо дві шукані точки В і С.
Завдання 705
Накресліть коло із центром O і радіусом 3 см. Позначте на ньому точки A і B такі, що AB = 3 см. Знайдіть периметр трикутника AOB.
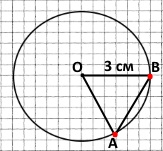
Р = 3 см + 3 см + 3 см = 9 см
Завдання 706
Накресліть коло й позначте на ньому три точки A, B і C.
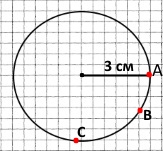
При цьому утворилося шість дуг: АВ, ВС, СА, АВС, АСВ, ВАС
Завдання 707
Накресліть коло радіуса 3 см із центром O. Проведіть промінь з початком у точці O та позначте на ньому точку A, віддалену від точки O на 5 см. Проведіть коло з центром у точці A, радіус якого:
1) 2 см; Має одну спільну точку В.
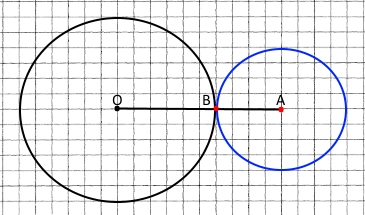
2) 2 см 5 мм; Мають дві спільні точки С і D
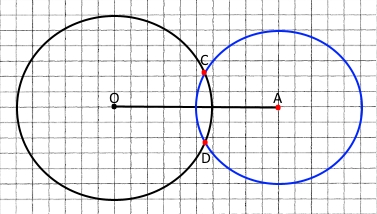
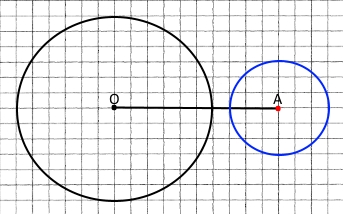
3) 1 см 5 мм. Не мають спільних точок.
Завдання 708
Накресліть коло та трикутник так, щоб сторони трикутника були хордами кола.
Завдання 709
Накресліть коло, проведіть його діаметр AB. Позначте на колі точки C і D та сполучіть кожну з них із кінцями діаметра AB.
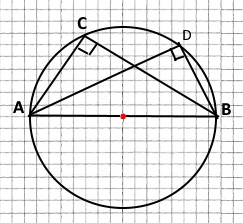
Величина кожного з кутів ACB і ADB дорівнює 90 градусів.
Завдання 710
Накресліть коло із центром O і проведіть його діаметр AB. Проведіть ще один діаметр, який позначте CD, так, щоб кут AOD був прямий. Проведіть хорди AC, BC, BD і AD.
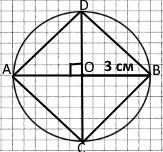
Чотирикутник ABCD є квадратом.
Завдання 711
Радіус кола з центром A дорівнює 9 см, а радіус кола з центром B — 2 см (рис. 40). Знайдіть відстань між центрами цих кіл.
1) АВ = 9 см + 2 см = 11 см
2) АВ = 9 см – 2 см = 7 см
Завдання 712
На рисунку OC = 6 см, BD = 2,5 см. Знайдіть довжину відрізка OK.
OK = OC – 2BD = 6 см – 2 • 2,5 см = 6 см – 5 см = 1 см
Завдання 713
Накресліть довільний трикутник. Проведіть три кола так, щоб сторони трикутника були їхніми діаметрами.
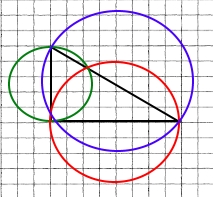
Завдання 714
Накресліть квадрат зі стороною 3 см. Проведіть чотири кола так, щоб сторони квадрата були їхніми діаметрами.
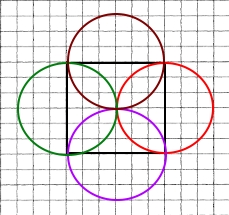
Завдання 715
1) Накресліть відрізок AB завдовжки 3 см. Знайдіть точку, віддалену від кожного з кінців відрізка AB на 2 см. Скільки існує таких точок? Дві точки.
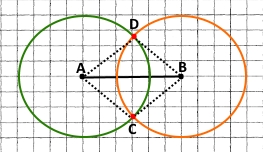
2) Накресліть відрізок CD завдовжки 3 см 5 мм. Знайдіть точку, віддалену від точки C на 2 см 5 мм, а від точки D — на 3 см. Скільки існує таких точок? Дві точки.
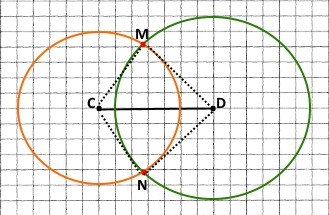
Завдання 716
За допомогою циркуля та лінійки побудуйте трикутник зі сторонами:
1) 3 см, 3 см і 4 см;
За допомогою лінійки будуємо відрізок АВ довжиною 4 см. З кінців відрізка АВ проводимо кола радіусом 3 см. З'єднаємо кінці відрізка АВ з однією з точок перетину кіл. Отримаємо трикутник АВС.
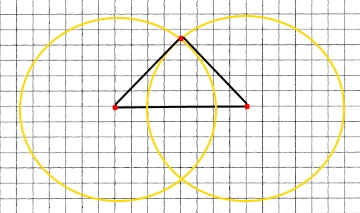
2) 3 см, 4 см і 5 см.
За допомогою лінійки будуємо відрізок АВ довжиною 5 см. З одного його кінця проводимо коло, радіус якого 3 см, а з другого — коло радіус якого 4 см. З'єднаємо кінці відрізка АВ з однією з точок перетину кіл. Отримаємо трикутник АВС.
Завдання 717
За допомогою циркуля та лінійки побудуйте трикутник зі сторонами:
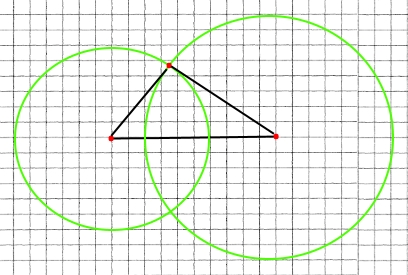
1) 5 см, 6 см і 4 см;
За допомогою лінійки будуємо відрізок АВ довжиною 6 см. З одного його кінця проводимо коло, радіус якого 5 см, а з другого — коло радіус якого 4 см. З'єднаємо кінці відрізка АВ з однією з точок перетину кіл. Отримаємо трикутник АВС.
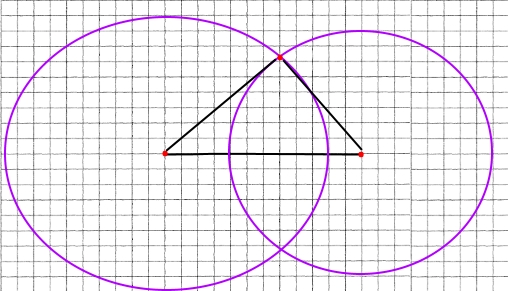
2) 2 см, 2 см і 2 см.
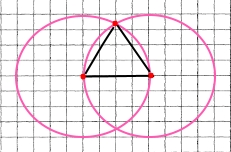
За допомогою лінійки будуємо відрізок АВ довжиною 2 см. З кінців відрізка АВ проводимо кола радіусом 2 см. З'єднаємо кінці відрізка АВ з однією з точок перетину кіл. Отримаємо трикутник АВС.
Завдання 718
Установіть, чи можна побудувати трикутник зі сторонами:
1) 2 см, 6 см і 7 см; Так, бо 2 см + 6 см > 7 см.
2) 2 см, 6 см і 8 см; Ні, бо 8 см = 2 см + 6 см
3) 2 см, 6 см і 9 см. Ні, бо 2 см + 6 см < 9 см.
Властивість довжини трьох відрізків, щоб вони могли слугувати сторонами трикутника: сума будь-яких двох сторін трикутника має бути більшою, ніж його третя сторона.
Завдання 719
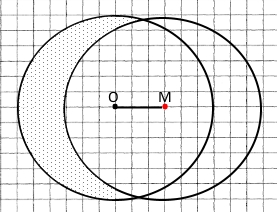
У крузі із центром O позначили точку M. Як розрізати цей круг:
1) на три частини; Вирізати два різні круги з центрами в точках О і М, а потім поміняти їх місцями.
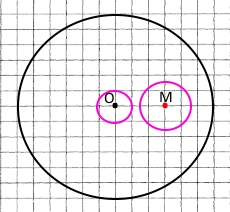
2) на дві частини так, щоб із них можна було скласти новий круг, у якому позначена точка M була б його центром? Необхідно побудувати коло з центром у точці М та радіусом рівним радіусу вихідного кола з центром у точці О. Розрізати коло з центром у точці О по дузі, утвореною колом із центром у точці О. Відрізані частини приєднати одна до одної зі зворотного боку.
Завдання 720
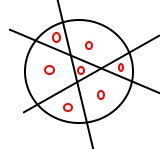
На торті кондитер розмістив 7 троянд із крему (рис. 42). Як трьома прямолінійними розрізами поділити торт на 7 порцій, на кожній з яких була б одна троянда?
Вправи для повторення
Завдання 721 Степінь числа
1) 7² = 7 • 7 = 49
2) 0,4² = 0,4 • 0,4 = 0,16
3) 1,2² = 1,2 • 1,2 = 1,44
4) (1/3)² = 1/3 • 1/3 = 1/9
5) (2 2/9)² = (20/9)² = 20/9 • 20/9 = 400/81 = 4 76/81
Завдання 722
Першого дня продали 500 кг яблук, а другого — 420 кг. На скільки відсотків менше продали яблук другого дня, ніж першого?
Розв'язання
1) 500 – 420 = 80 (кг) – настільки менше продали яблук;
2) 80 : 500 • 100% = 16%
Відповідь: на 16%.
Завдання 723
(6,8 – 5 5/9) : (2 13/30 – 2 1/12) • 3,6 = 12,8
1) (6,8 – 5 5/9) = 6 8/10 – 5 5/9 = 6 4/5 – 5 5/9 = 6 36/45 – 5 25/45 = 1 11/45
2) 2 13/30 – 2 1/12 = 2 26/60 – 2 5/60)= 21/60
3) 1 11/45 : 21/60 • 3,6 = 1 11/45 : 21/60 • 3 3/5 = 56/45 • 60/21 • 18/5 = 64/5 = 12 4/5 = 12,8
Задача від Мудрої Сови
Завдання 724
Діти збирали в лісі гриби. Вийшовши з лісу, вони стали парами — хлопчик з дівчинкою, причому в хлопчика грибів або вдвічі більше, або вдвічі менше, ніж у дівчинки. Чи могло так статися, що всі діти разом зібрали 500 грибів? Ні, не могло таке статися. З умови випливає, що кількість грибів, зібрана кожною парою, кратна 3. Отже, числу 3 кратна і загальна кількість усіх зібраних грибів, а 500 не ділиться націло на 3.
