
Завдання 860
|
1) |19| = 19; Так
|
2) |–6,4| = –6,4. Ні
|
3) |–7,28| = 7,28. Так
|
Завдання 861 Модуль числа
|
|2| = 2
|–3| = 3
|4,3| = 4,3
|
|12,6| = 12,6
|−17 1/7| = 17 1/7
|–36| = 36
|
|0| = 0
|5 11/16| = 5 11/16
|–129| = 129
|
Завдання 862
1) |5,1| + |–9,9| = 5,1 + 9,9 = 15
3) |–9,6| : |32| = 9,6 : 32 = 0,3
2) |−7/9| − |4/15| = 7/9 − 4/15 = 35/45 − 12/45 = 23/45
4) |8/9| • |27/32| = 8/9 • 27/32 = 3/4
Завдання 863
1) |–3,5| – |2,6| = 3,5 – 2,6 = 0,9
2) |20/21| + |−5/7| = 20/21 + 5/7 = 20/21 + 15/21 = 35/21 = 1 14/21 = 1 2/3
3) |–2,1| • |–3,7| = 2,1 • 3,7 = 7,77
4) |–1/16| : |–1 1/4| = 1/16 : 1 1/4 = 1/16 : 5/4 = 1/16 • 4/5 = 1/20
Завдання 864
1) якщо a = −5 1/3, b = 1 5/9, тоді
|−5 1/3| : |1 5/9| = 5 1/3 : 1 5/9 = 16/3 : 14/9 = 16/3 • 9/14 = 24/7 = 3 3/7
2) якщо a = 1,38, b = –0,4 , тоді |1,38| : |–0,4| = 1,38 : 0,4 = 3,45
Завдання 865
1) якщо a = –0,14, b = 0,1, тоді |a| – |b| = |–0,14| – |0,1| = 0,14 – 0,1 = 0,04
2) a = −2 11/12, b = −1 17/18, тоді
|−2 11/12| – |−1 17/18| = 2 11/12 – 1 17/18 = 2 33/36 – 1 34/36 = 1 69/36 – 1 34/36 = 35/36
Завдання 866, 867
|
1) 14
2) 4,6
|
1) –16
2) –0,8
|
Завдання 868
−12; −6,8; 1/19; 349,6
Завдання 869
1) протилежні числа — це числа, які мають різні знаки; Ні
2) протилежні числа — це числа, які мають різні знаки та рівні модулі. Так
Завдання 870 Рівняння
|
1) |x| = 12, х = –12 або х = 12
2) |x| = –8, рівняння не має розв'язку
|
3) |x| = 0, х = 0
4) |–x| = 2,4, х = –2,4 або х = 2,4
|
Завдання 871
1) |x| = 5
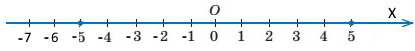
2) |x| = 7
3) |x| = 2,5
4) |x| = 0
5) |x| = 3,5
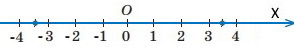
6) |x| = 4
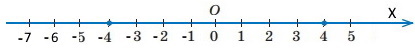
Завдання 872 Рівняння
1) |x| = 3,7; х = –3,7 або х = 3,7
2) |x| = –7,4; Рівняння не має розв'язків
3) |x| = 0,1. х = –0,1 або х = 0,1
Завдання 873
Числа у у порядку спадання їхніх модулів: 17,6; 8,6; 6,8; 2,2; 0,9; 0
Завдання 874
Числа у порядку зростання їхніх модулів: 0,4; 2,8; 3; 4,7; 9,4; 10,5
Завдання 875
Запишіть усі цілі числа, модулі яких менші від 3,6: –3; –2; –1; 0; 1; 2; 3
Завдання 876
Три додатних і три від’ємних цілих числа, модулі яких більші за 9,2:
10, 11, 12 і –10, –11, –12
Завдання 877
Позначте на координатній прямій цілі значення x, при яких є правильною нерівність:
1) |x| < 4, якщо цілі х = –3; –2; –1; 0; 1; 2; 3

2) 1,2 < |x| < 5, якщо цілі х = –4; –3; –2; 2; 3; 4

Завдання 878
Позначте на координатній прямій цілі значення x, при яких є правильною нерівність:
1) |x| < 6,1, якщо цілі числа х = –6; –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5; 6
2) 3,4 < |x| < 5,2, якщо цілі числа х = -5; -4; 4; 5
Завдання 879
Для якого числа одночасно виконуються рівності |a| = a і |a| = –a? 0
Завдання 880
Чи існує таке число a, що:
1) Чи існує таке число a, що |a| = –|a|; Так, а = 0
2) Чи існує таке число a, що |–a| = –|a|. Так, а = 0
Завдання 881
Якщо |a| = 7, тоді а = -7 і а = 7, тому відстань від точки A (a) до точки B (4): 11 і 3
Завдання 882
Якщо |a| = 4, тоді а = -4 і а = 4, тому відстань від точки A (a) до точки B (–2): 2 і 6
Завдання 883
1) якщо a = b, то |a| = |b|; Так
2) якщо |a| = |b|, то a = b; Ні
3) якщо a = –b, то |a| = |b|; Так
4) якщо a = b, то |a| = b; Ні
5) якщо |a| = |b|, то a = b або a = –b; Так
6) якщо a — ціле число, то |a| — натуральне число? Ні
Вправи для повторення
Завдання 884
За 1 год надрукували 5/8 рукопису. За скільки годин надрукують увесь рукопис?
Розвязання
1 : 5/8 = 1 • 8/5 = 8/5 = 1,6 год = 1 год 36 хв
Відповідь: 1 год 36 хв.
Завдання 885
Знайдіть відстань між двома містами, якщо 4/9 цієї відстані на 20 км менші, ніж уся відстань.
Розвязання
Нехай уся відстань х км. Складаємо рівняння.
х - 4/9х = 20
5/9х = 20
х = 20 : 5/9
х = 20 • 9/5
х = 36
Відповідь: 36 км.
Завдання 886
0,9 • (1 5/9 – 4/9 : (5/8 + 3/8 : 3)) = 13/15
1) 3/8 : 3 = 3/8 • 1/3 = 1/8
2) 5/8 + 1/8 = 6/8 = 3/4
3) 4/9 : 3/4 = 4/9 • 4/3 = 16/27
4) 1 5/9 – 16/27 = 14/9 – 16/27 = 42/27 – 16/27 = 26/27
5) 9/10 • 26/27 = 13/15
Завдання 887 Порівняня дробових чисел
1) 6/7 = 18/21, 18/21 > 17/21, 6/7 > 17/21
3) 5/9 = 35/63 i 4/7 = 36/63, 35/63 < 36/63, 5/9 < 4/7
5) 0,02 > 0,019
2) 7/12 = 35/60 i 11/15 = 44/60, 35/60 < 44/60, 7/12 < 11/15
4) 3,4 > 3,38
6) 0,001 > 0
Завдання 888
5 5/8 = 5,625; 5 3/5 = 5,6; 5,7; 4 1/2 = 4,5; 6,1; 4 9/16 = 4,5625
У порядку зростання числа: 4 1/2; 4 9/16; 5 3/5; 5 5/8; 5,7; 6,1
Задача від Мудрої Сови
Завдання 889
У деякому весняному місяці понеділків більше, ніж вівторків, а неділь більше, ніж субот. Який день тижня був 7-го числа цього місяця? Який це місяць? Оскільки в цьому весняному місяці неділь більше, ніж субот, і понеділків більше, ніж вівторків, то цей місяць починається у неділю і закінчується у понеділок. Тобто у ньому 30 днів. Серед весняних місяців 30 днів тільки у квітні. Якщо у неділю було перше число, то сьоме число припадає на суботу.
Відповідь: субота; квітень.