Завдання 1183 Парпендикулярні прямі

NР ⊥ МК; NК ⊥ КР; NK ⊥ МN; МР ⊥ КР; МР ⊥ МN.

Завдання 1184

АС ⊥ КЕ; FТ ⊥ МО.

Завдання 1185

а)	б)	в)	г)

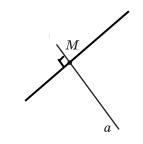Проведіть пряму d і позначте точку M, яка їй не належить. За допомогою косинця проведіть через точку M пряму, перпендикулярну до прямої d.

Завдання 1187

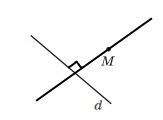
Проведіть пряму c і позначте точку K, яка їй належить. Користуючись косинцем, проведіть через точку K пряму, перпендикулярну до прямої c.

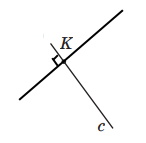
Завдання 1188

Накресліть прямокутник ABCD, сполучіть точки A і C. Проведіть через точку B пряму, перпендикулярну до прямої AC.

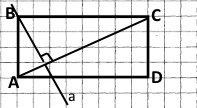
Завдання 1189

1) гострокутний;	2) тупокутний;	3) прямокутний.

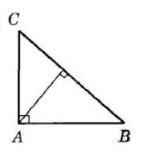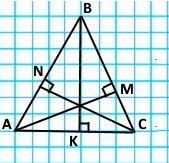
Накресліть кут ABK. Позначте на промені BK точку C і проведіть через неї прямі, перпендикулярні до прямих AB і BK.

1) 73°	2) 146°

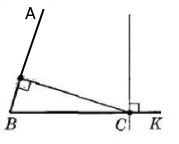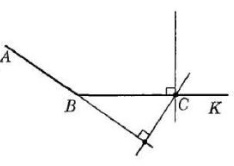Перерисуйте в зошит рисунок 128. Проведіть через точку O прямі, перпендикулярні до прямих

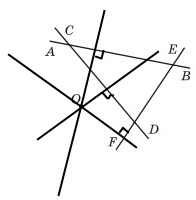
Завдання 1192

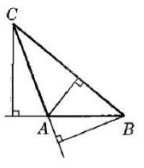
Накресліть гострокутний трикутник і позначте всередині нього точку. Проведіть через цю точку прямі, перпендикулярні до сторін трикутника.

Завдання 1193

Накресліть чотирикутник ABCD, у якому:

1) AB ⊥ AD;	2) AB ⊥ AD, AB ⊥ BC;	3) AB ⊥ AD, BC ⊥ CD.

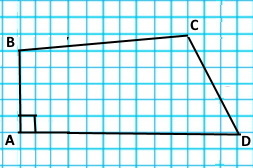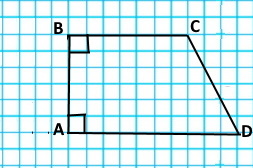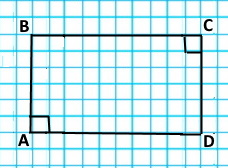Визначте на око, а потім перевірте за допомогою косинця, які з прямих, зображених на рисунку 129, перпендикулярні.

a ⊥ m, b ⊥ k, c ⊥ s, d ⊥ p

Завдання 1195

Накресліть два перпендикулярних відрізки так, щоб вони:

1) перетиналися;	2) не мали спільних точок;	3) мали спільний кінець.

1) перетиналися;	2) не мали спільних точок;

На рисунку 130 AB ⊥ CD, ∠MOC + ∠BOK = 130°, ∠BOK = 130°, ∠COK = 42°. Обчисліть градусну міру:

∠МОА = 180° – (∠МОС + ∠ВОК + ∠СОК) = 180° – (130° + 42°) = 8°

1) ∠МОК = ∠МОС + ∠СОК = (∠АОС – ∠МOА) + ∠СОК = (90° – 8°) + 42° = 124°

2) ∠МОD = ∠МОА + ∠АОD = 8° + 90° = 98°

Завдання 1198

На рисунку 131 AC ⊥ DK, OB ⊥ BF, ∠DBO = ° 54 . Обчисліть градусну міру кута ABF.

∠ОВС = ∠DВС – ∠DВО = 90° – 54° = 36°

∠СВF = ∠ОВF – ∠ОВС = 90° – 36° = 54°

∠АВF = ∠АВC – ∠СВF = 180° – 54° = 126°

Завдання 1199

Як побудувати перпендикулярні прямі, користуючись шаблоном кута, який дорівнює: 

1) 15°; Відкласти послідовно 6 кутів по 15° (15° • 6 = 90°) і через сторони кута провести прямі.

 2) 18°? Відкласти послідовно 5 кутів по 18° (18° • 5 = 90°) і через сторони кута провести прямі.

Завдання 1200

Користуючись косинцем і шаблоном кута 17°, побудуйте кут, градусна міра якого дорівнює:  

1) 5°; Від сторони прямого кута відкласти послідовно 5 разів кут 17° (17° • 5 = 85°). Той кут, що залишиться, буде 5° (90° - 85° = 5°).

2) 12°. Від сторони прямого кута відкласти послідовно 6 разів кут 17° (17° • 6 = 102°). Той кут, що залишиться дальше від прямого кута, буде 12° (102° - 90° = 12°).

Завдання 1201

Користуючись косинцем і шаблоном кута 20°, побудуйте кут, градусна міра якого дорівнює 10°. Від сторони прямого кута відкласти послідовно 4 рази кут 20° (20° • 4 = 80°). Той кут, що залишиться, буде 10° (90° - 80° = 10°).

Вправи для повторення

Завдання 1202

Сума цифр двоцифрового числа дорівнює 8, кількість десятків у 3 рази менша від кількості одиниць. Знайдіть це число.

Розв'язання

Нехай кількість десятків двоцифрового числа x, тоді кількість одиниць Зх. Cкладаємо рівняння:

Зх + х = 8

4х = 8

х = 2 – кількість десятків двоцифрового числа;

З • 2 = 6 – кількість одиниць двоцифрового числа.

Відповідь: двоцифрове число 26.

Завдання 1203

Чи є правильним твердження, що |a| + a = 2a при будь-якому значенні a? 

Ні, бо якщо a < 0, тоді |a| + a = –а + а = 0

Завдання 1205

За тиждень в офісі витрачають 1400 аркушів паперу. Яку найменшу кількість пачок паперу потрібно купити, щоб забезпечити роботу офісу протягом 6 тижнів, якщо в одній пачці міститься 500 аркушів?

Розв'язання

1) 1400 • 6 = 8400 (арк.) – витрачають аркушів за 6 тижнів;

2) 8400 : 500 = 16,8 ≈ 17 (п.) – потрібно пачок купити.

Відповідь: 17 пачок.

Завдання 1206

Максим відвідує заняття із самбо по понеділках, четвергах і суботах, а його друг Антон — уроки музики по вівторках, середах і п’ятницях. Заповніть таблицю з розкладом занять Максима й Антона, якщо відомо, що 11 і 15 січня в Антона уроки музики.

На шахівницю пролили фарбу. Чи може кількість заплямованих фарбою клітинок бути на 17 меншою від кількості клітинок, що залишилися чистими?

Розв'язання

Нехай кількість заплямованих х клітинок, тоді кількість чистих (х + 17) клітинок. Складаємо рівняння:

х + х + 17 = 64

2х = 47

х = 47 : 2

х = 23,5. Оскільки х має виражатися цілим числом, тому не може кількість заплямованих фарбою клітинок бути на 17 меншою від кількості клітинок, що залишилися чистими.

Відповідь: не може.

Інші завдання дивись тут...