Завдання 368 Трикутники
|
Трикутник MNP
|
Трикутник DRT
|
|
|
Вершини
Сторони
Кути
|
M, N, P
MN, NP, PN
M, N, P
|
D, R, T
DR, RT, TD
D, R, T
|
Завдання 369
| 1) різносторонній BAK |
2) рівнобедрений COD
|
3) рівносторонній LMT
|
Завдання 370
1) AB = 3 см, BC = 8 см, CA = 8 см; Рівнобедрений
2) AB = 15 м, BC = 15 м, CA = 15 м. Рівносторонній
Завдання 371
1) гострокутний трикутник; NML
2) тупокутний трикутник; ABC
3) прямокутний трикутник. XZY
Завдання 372
Назвіть вид трикутника АВC, якщо:
1) ∠А = 90°, ∠В = 20°, ∠С = 70°; Прямокутний
2) ∠А = 45°, ∠В = 65°, ∠С = 70°; Гострокутний
3) ∠А = 14°, ∠В = 126°, ∠С = 40°; Тупокутний
4) ∠А = 45°, ∠В = 45°, ∠С = 90°. Прямокутний, рівнобедрений
Завдання 373
Чи може сума всіх кутів трикутника дорівнювати:
| 1) 100°; Ні |
2) 170°; Ні
|
3) 180°; Так
|
4) 190° Ні
|
Завдання 374
Дано трикутник АВС. Знайдіть невідому величину за таблицею 19.
| АВ |
8 см
|
6 м
|
25 см
|
12 м
|
| АС |
4 см
|
8 м
|
25 см
|
20 м
|
| ВС | 5 см | 11 м | 25 см | 20 м |
| Р | 17 см | 25 см | 75 см | 52 см |
|
8 + 4 + 5 = 17 (см) 6 + 8 + 11 = 25 (см) |
25 • 3 = 75 (см) 12 + 20 + 20 = 52 (см) |
|||
Завдання 375
Обчисліть периметр трикутника АВС, якщо:
1) АВ = СВ = АС = 10 см; Р = 10 • 3 = 30 (см)
2) АВ = 6 м, СВ = 6 м, АС = 10 м; Р = 6 + 6 + 10 = 22 (м)
3) АВ = 12 см, СВ = 13 см, АС = 5 см. Р = 12 + 13 + 5 = 30 (см)
Завдання 376
У трикутнику АВС АВ = 6 см, сторона АС на 3 см довша за АВ, а сторона ВС на 4 см довша за АС. Знайдіть периметр трикутника.
Розв’язання
1) 6 + 3 = 9 (см) – довжина сторони АС;
2) 9 + 4 = 13 (см) – довжина сторони ВС;
3) 6 + 9 + 13 = 28 (см) – периметр трикутника.
Відповідь: 28 см.
Завдання 377
У трикутнику АВС СВ = 12 см, сторона АС удвічі довша за СВ, сторона АВ на 6 см довша за АС. Знайдіть периметр трикутника.
Розв’язання
1) 12 • 2 = 24 (см) – довжина сторони АС;
2) 24 + 6 = 30 (см) – довжина сторони АВ;
3) 12 + 24 + 30 = 66 (см) – периметр трикутника.
Відповідь: 66 см.
Завдання 378
У трикутнику АВС АВ = 18 см, сторона АС на 5 см менша від АВ, сторона ВС на 6 см менша від АС. Знайдіть периметр трикутника.
Розв’язання
1) 18 – 5 = 13 (см) – довжина сторони АС;
2) 13 – 6 = 7 (см) – довжина сторони ВС;
3) 18 + 13 + 7 = 38 (см) – периметр трикутника.
Відповідь: 38 см.
Завдання 379
Побудуйте довільний трикутник. Виміряйте його сторони та визначте його вид. Знайдіть периметр трикутника.
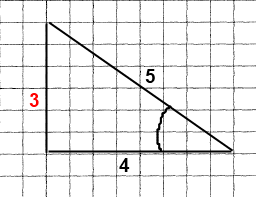
Розв’язання
3 + 4 + 5 = 12 (см) – периметр трикутника.
Відповідь: 12 см; трикутник прямокутний.
Завдання 380
Знайдіть периметр рівностороннього трикутника ABC, якщо:
1) AB = 21 мм; 21 • 3 = 63 (мм)
2) AC = 4 м; 4 • 3 = 12 (м)
3) AB = 17 см. 17 • 3 = 51 (см)
Завдання 381
Знайдіть периметр рівностороннього трикутника, якщо його сторона дорівнює 15 см.
Розв’язання
15 • 3 = 45 (см)
Відповідь: 45 см.
Завдання 382
Знайдіть довжини сторін рівностороннього трикутника, якщо його периметр дорівнює 36 см.
Розв’язання
36 : 3 = 12 (см)
Відповідь: 12 см.
Завдання 383
Знайдіть довжини сторін рівностороннього трикутника, якщо його периметр дорівнює 72 м.
Розв’язання
72 : 3 = 24 (м)
Відповідь: 24 м.
Завдання 384 Чи існує трикутник зі сторонами:
|
1) 1 см, 1 см, 2 см; Ні, бо 2 = 1 + 1
2) 3 см, 8 см, 8 см; Так
3) 4 см, 3 см, 5 см; Так
|
4) 6 см, 10 см, 4 см; Ні, бо 10 = 6 + 4
5) 12 см, 4 см, 15 см; Так
6) 21 см, 19 см, 5 см? Так
|
Завдання 385
|
1) 9 см, 10 см, 11 см; Так
2) 4 см, 4 см, 4 см; Так
|
3) 10 см, 2 см, 8 см; Ні, бо 10 = 2 + 8
4) 13 см, 7 см, 5 см? Так
|
Завдання 386
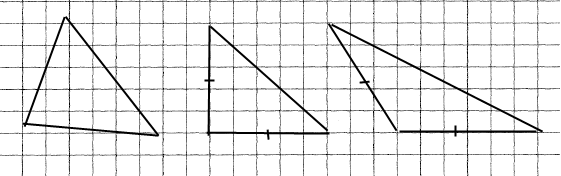
Трикутники: гострокутний, прямокутний, тупокутний.
Завдання 387
|
А
|
60°
|
60°
|
60°
|
45°
|
135°
|
|
В
|
30°
|
20° | 42° | 90° | 20° |
|
С
|
90° | 100° | 78° | 45° | 25° |
|
180° - 60° - 30° = 90° 180° - 60° - 100° = 20° 180° - 60° - 42° = 78° |
180° - 90° - 45° = 45° 180° - 135° - 20° = 25° |
||||
Завдання 388
Дано трикутник АВС. Знайдіть кут С, якщо:
1) ∠А = 35°, ∠В = 90°; ∠С = 180° – ∠А – ∠В = 180° – 35° – 90° = 55°
2) ∠А = 120°, ∠В = 30°. ∠С = 180° – ∠А – ∠В = 180° – 120° – 30° = 30°
Завдання 389
Кут А трикутника дорівнює 40°, а кут С — удвічі більший за кут А. Знайдіть кут В. Визначте вид трикутника.
Розв’язання
1) 40° • 2 = 80° – кут С;
2) 180° – (40° + 80°) = 60° – кут В.
Відповідь: 60°; трикутник гострокутний.
Завдання 390
Кут С трикутника дорівнює 135°, а кут В — на 105° менший від кута С. Знайдіть кут А. Визначте вид трикутника.
Розв’язання
1) 135° – 105° = 30° – кут В;
2) 180° – (135° + 30°) = 15° – кут А.
Відповідь: 15°, трикутник тупокутний.
Завдання 391
Кут А трикутника дорівнює 70°, а кут С — на 10° більший за кут А. Знайдіть кут В. Визначте вид трикутника.
Розв’язання
1) 70° + 10° = 80° – кут С;
2) 180° – (70° + 80°) = 30° – кут В.
Відповідь: 30°, трикутник гострокутний.
Завдання 392
Скільки трикутників зображено на малюнку 140? 20 трикутників.
Завдання 393
Сторона АВ трикутника АВС дорівнює 10 см. Сторона АС — удвічі більша за АВ і на 6 см менша, ніж ВС. Знайдіть периметр трикутника.
Розв’язання
1) 10 • 2 = 20 (см) – сторона АС;
2) 20 + 6 = 26 (см) – сторона ВС;
3) 10 + 20 + 26 = 56 (см) – периметр трикутника.
Відповідь: 56 см.
Завдання 394
Одна сторона рівнобедреного трикутника дорівнює 10 см, а інша — на 4 см більша. Знайдіть периметр трикутника. Скільки розв’язків має задача?
Розв’язання
|
Перший розв'язок
|
Другий розв'язок
|
|
1) 10 + 4 = 14 (см) – інша сторона;
2) 14 • 2 = 28 (см) (см) – рівні сторони;
3) 10 + 28 = 38 (см)
Відповідь: 38 см.
|
1) 10 + 4 = 14 (см) – інша сторона;
2) 10 • 2 = 20 (см) – рівні сторони;
3) 14 + 20 = 34 (см)
Відповідь: 34 см.
|
Завдання 395
Сторона ВС трикутника АВС дорівнює 17 см. Сторона АС на 8 см більша за ВС і на 6 см менша від АВ. Знайдіть периметр трикутника.
Розв’язання
1) 17 + 8 = 25 (см) – сторона ВС;
2) 25 + 6 = 31 (см) – сторона АВ;
3) 17 + 25 + 31 = 73 (см) – периметр трикутника.
Відповідь: 73 см.
Завдання 396
Сторони АВ і СВ трикутника АВС дорівнюють по 10 см. Знайдіть довжину сторони АС, якщо периметр трикутника дорівнює 25 см.
Розв’язання
1) 10 + 10 = 20 (см) – сума двох сторін АВ і СВ;
2) 25 – 20 = 5 (см) – довжина сторони АС.
Відповідь: 5 см.
Завдання 397
У трикутнику АВС АВ = 20 см, сторона АС на 5 см менша, ніж сторона АВ. Знайдіть довжину сторони ВС, якщо периметр трикутника АВС дорівнює 65 см.
Розв’язання
1) 20 – 5 = 15 (см) – довжина сторони АС;
2) 65 – (20 + 15) = 30 (см) – довжина сторони ВС.
Відповідь: 30 см.
Завдання 398
Чому дорівнює сторона рівностороннього трикутника, периметр якого вдвічі менший від периметра квадрата зі стороною 12 см?
Розв’язання
1) 12 • 4 = 48 (см) – периметр квадрата;
2) 48 : 2 = 24 (см) – периметр рівностороннього трикутника;
3) 24 : 3 = 8 (см) – довжина сторони рівностороннього трикутника.
Відповідь: 8 см.
Завдання 399
Є 8 паличок, довжина кожної з яких дорівнює 2 см. Чи можна з них скласти трикутник? Скільки різних трикутників можна отримати? Які їхні сторони?
Розв’язання
1) Можна скласти трикутник.
2) 2 • (3 + 3 + 2), або 2 • (1 + 1 + 6), або 2 • (1 + 2 + 5).
Завдання 400
Дано відрізки, довжини яких дорівнюють 6 см, 4 см, 2 см, 1 см, 8 см. Скільки трикутників можна утворити з даних відрізків?
Розв’язання
1) 6 см; 4 см; 2 см.
2) 4 см; 2 см; 1 см.
3) 1 см; 8 см; 2 см.
Відповідь: з даних відрізків можна утворити три трикутники.
Завдання 401
У прямокутному трикутнику ABC: ∠В — прямий, ∠A — на 56° більший за ∠С. Знайдіть кути трикутника.
Розв’язання
Нехай ∠С = х°, тоді ∠А = х° + 56°, а ∠В = 90°. Складаємо рівняння.
х + (х + 56) + 90 = 180
2х = 180 – 56 – 90
2х = 34
х = 34 : 2
х = 17 (°) – ∠С;
17 + 56 = 73 (°) – ∠А.
Відповідь: 17°, 73° і 90°.
Завдання 402
Кут А трикутника АВС дорівнює 60°. Кут С — удвічі більший за кут В. Знайдіть ∠В і ∠С.
Розв’язання
Нехай ∠В = х°, тоді ∠С = 2х°, а ∠А = 60°. Складаємо рівняння.
х + 2х + 60 = 180
3х = 180 – 60
3х = 120
х = 120 : 3
х = 40 (°) – ∠В;
40 • 2 = 80 (°) – ∠С.
Відповідь: 40° і 80°.
Завдання 403
Сторона рівнобедреного трикутника дорівнює 18 см, а його периметр — 42 см. Знайдіть інші сторони трикутника. Скільки розв’язків має задача?
|
1 випадок
|
2 випадок
|
|
1) 18 • 2 = 36 (см) – дві рівні сторони;
2) 42 – 36 = 6 (см) – інша сторона.
Відповідь: 6 см.
|
1) 42 – 18 = 24 (см) – сума рівних сторін.
2) 24 : 2 = 12 (см) – кожна з рівних сторін.
Відповідь: 12 см.
|
Завдання 404
Сторона АВ трикутника АВС на 7 см більша за сторону АС, яка на 6 см менша, ніж сторона ВС. Знайдіть сторони трикутника, якщо його периметр дорівнює 49 см.
Розв’язання
Нехай сторона АС дорівнює х см, тоді АВ дорівнює (х + 7) СМ, а ВС дорівнює (х + 6) см. Складаємо рівняння.
х + (х + 7) + (х + 6) = 49
3х = 49 – 6 – 7
3х = 36
х = 36 : 3
х = 12 (см) – сторона АС;
12 + 7 = 19 (см) – сторона АВ;
12 + 6 = 18 (см) – сторона ВС.
Відповідь: 12 см, 19 см і 18 см.
Завдання 405
У трикутнику ABC: AB + BC = 25 см, BC + CA = 26 см, CA + AB = 27 см. Знайдіть периметр трикутника ABC та кожну його сторону.
Розв’язання
1) 25 + 26 + 27 = 78 (см) – сума всіх сторін, взята двічі;
2) 78 : 2 = 39 (см) – сума всіх сторін;
3) 39 – 25 = 14 (см) – довжина сторони СА;
4) 26 – 14 = 12 (см) – довжина сторони ВС;
5) 27 – 14 = 13 (см) – довжина сторони АВ;
Відповідь: 13 см, 12 см і 14 см.
Завдання 406
У трикутнику ABC: ∠В + ∠С = 98°, ∠В + ∠А = 130°. Знайдіть кути трикутника ABC.
Розв’язання
1) 180° – 98° = 82° – ∠А;
2) 130° – 82° = 48° – ∠В;
3) 98° – 48° = 50° – ∠С.
Відповідь: 82°, 48° і 50°.
Завдання 407
Папір має форму прямокутника, одна сторона якого дорівнює 4 см, а друга — 9 см. Розріжте прямокутник на дві рівні частини так, щоб можна було, склавши їх, одержати трикутник.
Завдання 408
На уроці трудового навчання дівчата одержали завдання пошити трикутну косинку, розміри якої: 50 см, 50 см, 75 см. Марійка виконала завдання точно. У Даринки кожна сторона косинки вийшла на 1 см коротшою, а в Оксани — на 5 см довшою. Дівчата вирішили оздобити свої косинки мереживом.
1) Скільки сантиметрів мережива потрібно купити кожній дівчинці, щоб обшити свою косинку (припусками для зшивання знехтувати)?
Розв’язання
50 + 50 + 75 = 175 (см) – потрібно купити мережива Марійці;
49 + 49 + 74 = 172 (см) – потрібно купити мережива Даринка;
55 + 55 + 80 = 190 (см) – потрібно купити мережива Оксанці.
2) Кому з дівчат доведеться купувати більше мережива й на скільки сантиметрів більше?
190 – 175 = 15 (см) – на стільки більше доведеться купити мережива Оксанці.
3) Хто з дівчат витратить найменше мережива? Даринка