Завдання 708 Провідміняй слово
|
Відмінки |
а) аргумент |
б) функція |
в) графік |
|
Називний Родовий Давальний Знахідний Орудний Місцевий |
аргумент аргументу аргументу аргумент аргументом аргументу |
функція функції функції функцію функцією функції |
графік графіка графіку графік графіком графіку |
Завдання 709
Графіками функцій є лінії, зображені на малюнку першому і третьому.
Завдання 710
Доведи, що графік функції у = x² + 1 не перетинає вісь абсцис.
При будь–яких значеннях х значення у ≠ 0, отже, графік не перетинає вісь х.
Завдання 711
Чи перетинає вісь абсцис графік функції у = x² – 9?
X² – 9 = 0
(х – 3)(х + 3) = 0
х = 3 або х = –3 Отже, графік перетинає вісь х в точках (–3:0) і (3;0).
Завдання 712
Графік якої з функцій проходить через початок координат?
|
Відмінки |
а) аргумент |
б) функція |
|
а) у = 0,5x – 1 г) у = 6x + 2 |
б) у = –25x² ґ) у = 3 – 3x |
в) у = 3x д) у = x – 3x² |
Завдання 713
Яка з точок належить графіку функції у = 7х – 2? 7 • 1 – 2 = 5, тому В (1; 5)
Завдання 714
а) Температура була додатною впродовж часу від 11 год до 23 год, а
від'ємною впродовж часу від 0 год до 11 год, та від 23 год до 24 год.
б) –3°С було о 2 годині і 8 годині; –1°С було о 10 годині і о 23 годині 30 хвилин;
0°С було об 11 годині і о 23 годині; 2°С було 0 13 годині і о 21 годині.
в) О 6 год ранку було –4°С; о 14 год було 3°С; о 21 год було 2°С;
г) Температура знижувалася з 0 год до 6 год; з 18 год по 24 год; а підвищувалася з 6 год до 14 год.
ґ) Температура була сталою з 14 год до 18 год і дорівнювала 3°С.
д) Температура була нижча, ніж –3°С від 2 год до 8 год.
Завдання 715
Установи відповідність між графіками функцій (1–2) та їх областями значень (А–Г).
1) — В –4 ≤ y ≤ 4. Область визначення: –4 < x ≤ 5; функція зростаюча;
2) — А –2 ≤ y ≤ 4. Область визначення: –6 ≤ x ≤ 6; функція спадаюча.
ВИКОНАЙ ПИСЬМОВО РІВЕНЬ А
Завдання 716
Познач на координатній площині точки A(5;4), B(3;3), C(1;0), D(7;3), E(–2;5), F(–2;–2).
Побудуй прямі AC, BD, EF. Знайди координати точок, у яких ці прямі попарно перетинаються.
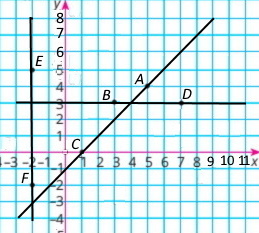
Прямі АС і BD перетинаються в точці (4; 3) прямі АС і EF перетинаються в точці (–2; –3).
Завдання 717
За графіком на малюнку знайди:
а) якщо х=–1, то у = 3; якщо х=0, то у = 5; якщо х=3, то у = 1,5; якщо х=4, то у = 1;
б) у=–1, якщо х = –3; у=0, якщо х = –2; у=3, якщо х = –1 або x = 1,5; у=5, якщо х = 0.
Завдання 718
За графіком функції (мал. 17.11) заповни таблицю.
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
y |
–2 |
–1 |
0 |
2 |
2 |
0 |
–1 |
0 |
1,5 |
Завдання 719
За графіком функції (мал. 17.12) заповни таблицю.
|
x |
–1 |
–0,5 |
0 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
|
y |
–5 |
–4 |
–3 |
–1 |
0 |
1 |
2 |
3 |
4 |
Завдання 720
За малюнком 17.13 знайди:
а) якщо х=–3, то у = 3; якщо х=–1, то у = –1,5; якщо х=0, то у = –2;
якщо х=1, то у = –2; якщо х=4, то у = 2
б) у=–2, якщо х = 0 і х = 1; у=–1, якщо х = –1,5 і х = 2; у=0, якщо х = –2 і х = 3;
у=1, якщо х = –2,5 і х = 3,5; у=3, якщо х = –3 і х = 4,5
в) у – додатне, якщо –4 < х < 2 і 3 < х < 6
г) у – від'ємне, якщо –2 < х < 3
Завдання 721
На малюнку 17.14 зображено графік деякої функції. Знайди:
1. а) область визначення функції: –4 ≤ x ≤ 9
б) значення функції, яке відповідає значенню аргументу:
|
x |
–4 |
–3 |
0 |
2 |
3 |
4 |
6 |
|
y |
–3 |
0 |
3 |
2 |
1 |
0 |
–1,2 |
2. а) значення функції:
|
x |
–3,5 |
–3 або 4 або 8 |
–2 або 2 |
0 |
|
y |
–1 |
0 |
2 |
3 |
б) функція набуває додатних значень: –3 < x < 4 і від 8 < x ≤ 9
в) функція зростає: від –4 ≤ x < 0 і від 6 ≤ x ≤ 9
г) функція спадає: 0 < x ≤ 6
Завдання 722
Функцію задано формулою у = 1/2 х, якщо 1 ≤ х ≤ 12.
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
|
y |
0,5 |
1 |
1,5 |
2 |
2,5 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
Завдання 723
Визнач, чи належать графіку функції у = –2х – 1 точки:
а) A(5;1); Не належить, бо у = –2 • 5 – 1 = –11, –11 ≠ 1
б) B(–1;3); Не належить, бо у = –2 • (–1) – 1 = 1, 1 ≠ 3
в) C(–1;–3); Не належить, бо у = –2 • (–1) – 1 = 1, 1 ≠ –11
г) D(3;–7). Належить, бо у = –2 • 3 – 1 = –7
Завдання 724
Які з точок A(5;–4), B(3;3), C(1;0), D(1;7), E(–2; 5) належать графіку функції?
|
а) у = 5х + 2; D(1; 7) в) у = х² + 1; E(–2; 5) |
б) у = –х + 1; A(5; –4), C(1; 0) г) у = 10х – 3. D(1; 7) |
Завдання 725
а) у = –х, якщо –5 ≤ х ≤ 4;
|
x |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
|
y |
5 |
4 |
3 |
2 |
1 |
0 |
–1 |
–2 |
–3 |
–4 |
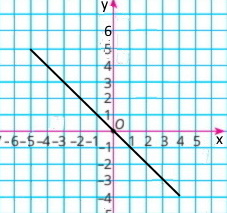
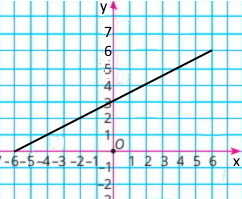
б) у = 0,5х + 3, якщо –6 ≤ х ≤ 6.
|
x |
–6 |
–5 |
–4 |
–3 |
–2 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
0 |
0,5 |
1 |
1,5 |
2 |
3 |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
Завдання 726
а) у = 2х, якщо –3 ≤ х ≤ 6;
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
y |
–6 |
–4 |
–2 |
0 |
2 |
4 |
6 |
8 |
10 |
12 |
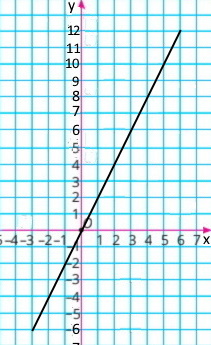
б) у = 2х – 1, якщо 0 ≤ х ≤ 7.
|
x |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
y |
–1 |
1 |
3 |
5 |
7 |
9 |
11 |
13 |
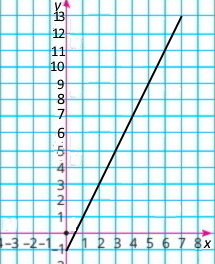
Завдання 727
Функцію у = 0,5х + 3 задано на множині натуральних чисел, не більших від числа 8.
|
x |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
|
y |
3,5 |
4 |
4,5 |
5 |
5,5 |
6 |
6,5 |
7 |
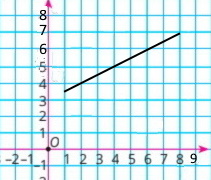
Завдання 728
Функцію у = 5 – х задано на множині цілих чисел, що задовольняють умову –7 ≤ х ≤ 7.
|
х |
–7 |
–6 |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
у |
12 |
11 |
10 |
9 |
8 |
7 | 6 | 5 | 4 | 3 | 2 | 1 | 0 | –1 | –2 |
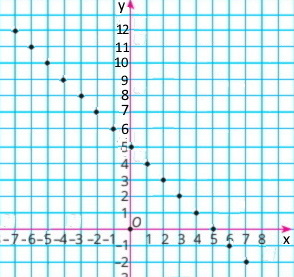
Завдання 729
Побудуй графік функції, заданої формулою у = 4 – 2х.
|
х |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
у |
8 | 6 | 4 | 2 | 0 | –2 | –4 | –6 | –8 |
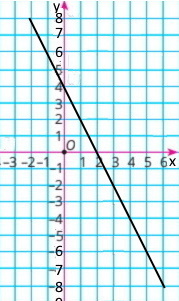
а) якщо x=0 , то у = 4; якщо х=1, то у = 2; якщо х=–1, то у = 6;
якщо х=2, то у = 0; якщо х=–2, то у = 8; якщо х=2,5, то у = –1
б) у=–6, якщо х = 5; у=–2, якщо х = 3; у=0, якщо х = 2; у=4, якщо х = 0
в) значення у додатні, якщо х < 2
г) значення у від'ємні, якщо х > 2
Завдання 730
Побудуйте графік функції, заданої формулою у = (x – 4)/2 = х/2 – 2 = 0,5х – 2
|
х |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
|
у |
–3 | –1,5 | –2 | –1,5 | –1 |
–0,3 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 |
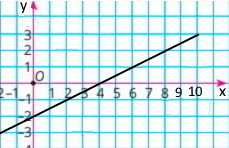
а) у=–3, якщо х = –2; у=–2, якщо х = 0; у=–1, якщо х = 2; у=0, якщо х = 4;
у=1, якщо х = 6; у=2, якщо х = 8; у=3, якщо х = 10
б) якщо x=–2, то у = –3; якщо x=0, то у = –2; якщо x=2, то у = –1;
якщо x=4, то у = 0; якщо x=6, то у = 1; якщо x=8, то у = 2
в) значення у додатні, якщо х > 4
г) значення у від'ємні, якщо х < 4
Завдання 731
Марина вирушила до Праги на конференцію. Вона взяли таксі з дому до аеропорту і з аеропорту до готелю. Яка частина графіка (мал. 17.15) відображає її рух на таксі до готелю? Частина V.
Завдання 732
На малюнку 17.16 зображено графіки руху пішохода (лінія a) і велосипедиста (лінія b). Користуючись графіком, визначте:
а) чи одночасно вони почали рухатись; Ні, велосипедист на 10 хв пізніше
б) чи сталою була швидкість кожного. Ні
Завдання 733
Графік якої функції проходить через точку A(3;–2)?
|
а) у = 3x – 8 г) у = 3x – 2 |
б) у = 2(x – 4) ґ) у = 2 1/3 x – 9 |
в) у = 7(1 – 5x) д) у = 1/7(1 –5x) |
Завдання 734
Визнач, чи належать графіку функції дані точки.
а) у = 0,5x + 4;
0,5 • 4 + 4 = 6, точка A(4;6) належить графіку функції;
0,5 • (–8) + 4 = 0, точка B(–8;0) належить графіку функції;
0,5 • 2 + 4 = 5, точка C(2;5) належить графіку функції;
б) у = –12x + 17;
–12 • 1 + 17 = 5, точка A(1;5) належить графіку функції;
–12 • (–1/3) + 17 = 21, точка B(–1/3;11) не належить графіку функції;
–12 • 0,5 + 17 = 11, точка C(0,5;11) належить графіку функції;
Завдання 735
Визнач, чи належать графіку функції дані точки.
а) y = x(x – 5);
0(0 – 5) = 0, точка A(0;–5) не належить графіку функції;
5(5 – 5) = 0, точка B(5;0) належить графіку функції;
0(0 – 5) = 0, точка C(0;0) належить графіку функції;
б) у = 4 – 8/x;
4 – 8/1 = –4, точка A(1;–4) належить графіку функції;
4 – 8/(1/2) = –12, точка B (1/2;0) не належить графіку функції;
4 – 8/4 = 2, точка C(4;–2) не належить графіку функції;
Завдання 736
Determine whether the points belong to the graph of the function.
a) y = 1/(x – 6);
1/(7 – 6) = 1, точка A(7;1) належить графіку функції;
1/(2 – 6) = –0,25, точка B(2;0) не належить графіку функції;
1/(3 – 6) = –1/3, точка C(3;1/3) не належить графіку функції;
b) y = (6 – x)²;
б) (6 – 7)² = 1, точка A(7;–1) не належить графіку функції;
(6 – 8)² = 4, точка B (8;4) належить графіку функції;
(6 – 4)² = 4, точка C(4;4) належить графіку функції;
Завдання 737
Функцію задано графічно (мал. 17.17).
а) у = х
|
x |
–1 |
0 |
1 |
2 |
|
y |
–1 |
0 |
1 |
2 |
б) y = –x – 1
|
x |
–1 |
0 |
1 |
2 |
|
y |
0 |
–1 |
–2 |
–3 |
в) y = –x² + 1
|
x |
–1 |
0 |
1 |
2 |
|
y |
0 |
1 |
0 |
–3 |
г) y = x²
|
x |
–1 |
0 |
1 |
2 |
|
y |
1 |
0 |
1 |
4 |
Завдання 738
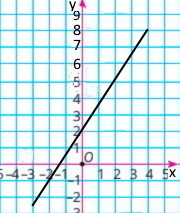
а) у = 1,5x + 2, якщо –3 ≤ x ≤ 4;
|
х |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
|
у |
–2,5 | –1 | –0,5 | 2 | 3,5 | 5 | 6,5 | 8 |
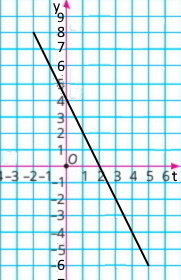
б) у = 4 – 2t, якщо –2 ≤ t ≤ 5.
|
х |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
у |
8 | 6 | 4 | 2 | 0 | –2 | –4 | –6 |
Завдання 739
а) у = (x + 6)/2 , якщо –8 ≤ x ≤ 14;
|
х |
–8 |
–7 |
–6 |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
8 |
9 |
10 |
11 |
12 |
13 |
14 |
|
у |
–1 | –0,5 | 0 | 0,5 | 1 | 1,5 | 2 | 2,5 | 3 | 3,5 | 4 | 4,5 | 5 | 5,5 | 6 | 6,5 | 7 | 7,5 | 8 | 8,5 | 9 | 9,5 | 10 |
б) у = –1/5 x = –0,2х, якщо –5 ≤ x ≤ 5.
|
х |
–5 |
–4 |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
|
у |
1 | 0,8 | 0,6 | 0,4 | 0,2 | 0 | –0,2 | –0,4 | –0,6 | –0,8 | –1 |
Завдання 740
а) у = 3 – 2x; функція спадна
б) у = 0,1x; функція зростаюча
в) у = (3x – 1)/5. функція зростаюча
Завдання 741
а) у = 2x – 5; функція зростаюча
б) у = –1/5 + 2x; функція зростаюча
в) у = (17 – x)/5. функція спадна
Завдання 742
Графік функції у = 2(1 – x). Знайди значення аргументу, при яких значення функції більші за –3 і менші від 7.
|
х |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
5 |
6 |
7 |
|
у |
8 |
6 |
4 |
2 |
0 |
–2 |
–4 | –6 | –8 | –10 | –12 |
Завдання 743
Графік функції у = 2x + m проходить через точку A(–2; 5). Знайди значення m.
2 • (–2) + m = 5
–4 + m = 5
m = 9
Завдання 744
Графік функції у = kx + 2 проходить через точку B(3; 8). Знайди значення k.
3k + 2 = 8
3k = 6
k = 2
Завдання 745
Функцію задано формулою у = x² – m. При якому значенні m графік цієї функції проходить через початок координат?
Точка початку координат (0;0), тому підставимо у функцію 0 = 0² – m, звідси m = 0.
ЦІКАВІ ЗАДАЧІ
Завдання 746
Установіть, який із графіків (мал. 17.18) відповідає кожній з описаних ситуацій.
а) На газоні росте трава, яку регулярно викошують (x – час, у – висота); в)
б) груша росте, потім її зривають і висушують (x – час, у – маса груші); а)
в) м’яч падає з деякої висоти на підлогу (x – час, у – висота м’яча). б)
Завдання 747
Доведи тотожність (n² + 1)² – (n² – 1)² = 4n² . Користуючись нею, доведи, що квадрат кожного парного числа дорівнює різниці квадратів двох деяких цілих чисел.
(n² + 1)² – (n² – 1)² = (n² + 1 – n² + 1)(n² + 1 + n² – 1) = 2 • 2n² = 4n²;
Тоді (2n)² = 4n² = (n² + 1)² – (n² – 1)² – квадрат кожного парного числа дорівнює різниці квадратів двох деяких цілих чисел.
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 748 Рівняння
|
а) (x + 3) = x + 9x x + 9x – x = 3 9x = 3 x = 1/3 |
б) (у – 5)² = у(у + 2) y² – 10y + 25 = y² + 2y 2y + 10y = 25 12y = 25 y = 25/12 у = 2 1/12 |
|
в) (1 – z) = 3 + z z + z = 1 – 3 2z = –2 z = –1 |
г) (7 – x)² – x² = 35 49 – 14x + x² – x² = 35 14x = 49 – 35 14x = 14 x = 1 |
Завдання 749
Підприємиця купує у фермера картоплю зі знижкою 10 % її оптової ціни, а продає картоплю в роздріб за ціною, що перевищує оптову на 10 %. Який відсоток прибутку має підприємиця?
Розв'язання
Позначимо оптову ціну картоплі через х, тоді вартість за ціною зі знижкою 10% дорівнює 0,9х грн, а вартість за ціною перевищення оптової ціни на 10% дорівнює 1,1х. Знайдемо рівницю вартості, тобто прибуток:
1) 1,1х – 0,9х = 0,2х – прибуток підприємиці;
2) 0,2х : х • 100% = 20% – відсотковий прибуток підприємиці.
Відповідь: 20%.
Завдання 750 Спрощення виразу
а) 10x²у(0,2x + 2y)(–0,2x + 2у) = 10x²y(4y² – 0,04x²) = 40x2y3 – 0,4x4y
б) (1/3 x – 2/3 y)(1/3 x + 2/3 y) • (–9ху) = (1/9x² – 4/9y²) • (–9ху) = –x3y + 4xy3