Інші завдання дивись тут...

Завдання 854 Лінійні рівняння 

А –2x = 5

Б 1/x = 2

В 3 – 2x = 0

Г 4x = 5 – x Не є лінійним

Завдання 855 Лінійне рівняння першого степеня

А 0x = 7

Б –2x = 0

В 3x² = 0

Г 0x = 0

Завдання 856

Має бути виведено повідомлення: безліч розв’язків.

 

Завдання 857 Корінь рівняння

а) 0x = 35    0 ≠ 35    Не існує

б) 0у = 13 – 13    0 = 0    Безліч

в) 2x = 3 + 2x    0 ≠ 3    Не існує

г) 2х + 5 = 3(х + 5)    2x + 5 = 3x + 15    x = –10

Завдання 858

Поясни, чому має безліч розв’язків рівняння.

а) x + 15 = x; 0х = –15, тому розв’язків немає

б) 3x – 7 = 3x; 0х = 7, тому розв’язків немає

в) 17 – x = 5 – x. 0х ≠ 12, тому розв’язків немає

 

Завдання 859

Поясни, чому має безліч розв’язків рівняння.

а) 3x = 2x + x; 0x = 0, тому х — будь – яке число

б) 6у = 7у – у; 0y = 0, тому х — будь–яке число

в) 8z + 2 = 3z + 2 + 5z. 0z = 0, тому х — будь–яке число

 

Завдання 860

Чи правильна схема, зображена на малюнку 20.2? Так

 

Завдання 861

а) 2 – 3x = 5 – 7x    2 + 7x = 5 + 3x    4x = 3    x = 3/4	б) 15 – 3x = 7x – 5    15 + 5 = 7x + 3x    20 = 10x    x = 2	в) 3x + 2(x + 7) = 2x    3x + 2x + 14 = 2x    5x + 14 = 2x    3x = –14    x = –14/3 = –4 2/3
г) 4(2 + x) – x = 3x + 9    8 + 4x – x = 3x + 9    8 + 3x = 3x + 9    0х = –1    Розв’язків немає	ґ) 1/3x = 6 – 1/2x    1/3x + 1/2x = 6    (2x + 3x)/6 = 6    5x/6 = 6    5x = 36    x = 36/5 = 7 1/5	д) (x – 4)/2 = 1     x – 4 = 2     x = 6

Завдання 862

а) 2x + x – 7x + 3=8    –4x + 3 = 8    –4x = 8 – 3     –4x = 5    x = –5/4 = –1 1/4	б) у – 5у=8 – у    у + у – 5у = 8    –3у = 8    у = –8/3 = –2 2/3
в) –c + 31(2 – c)=32c    –c + 62 – 31c = 32c    62 – c – 31c = 32c    62 = 32c + 32c    62 = 64c    c = 62/64    c = 31/32	г) 0,7=2(x + 3,5) – 2x    0,7 = 2x + 7 – 2x    0х = –6,3    Розв’язків немає

Завдання 863

а) 32x = –16    x = –16/32    x = –1/2	б) x + 4x = 5x    0x = 0    Розв’язків безліч	в) x = 3(x + 1) – 2x    x = 3x + 3 – 2x    0х = 3    Розв’язків немає
г) 2(5 – 8x) = –4(4x + 3)    10 – 16x = –16x – 12    0х = –22    Розв’язків немає	ґ) 2(x – 3) = 3(2x – 1)    2x – 6 = 6x – 3    –6 + 3 = 6x – 2x    –3 = 4x    x = –3/4	д) 4(5 – x) = –5x + 2    20 – 4x = –5x + 2    20 – 2 = –5x + 4x    18 = –x    x = –18

Завдання 864

а) –0,5у = –0,5    у = 1	б) 6x = 8 + 6x    6x – 6x = 8    0х = 8    Розв’язків немає	в) 4 – 3x = 8(1 – x)    4 – 3x = 8 – 8x    4 – 8 = –8x + 3x   –4 = –5x    x = 4/5
г) 2 – 5у = 5(1 – 2у)    2 – 5у = 5 – 10у    2 – 5 = –10у + 5у    –3 = –5у    у = 3/5	ґ) 8(9 – 2x) = 5(2 – 3x)    72 – 16x = 10 – 15x    72 – 10 = –15x + 16x    x = 62	д) 5(z + 3) = 8(10 – z)    5z + 15 = 80 – 8z    5z + 8z = 80 – 15    13z = 65    z = 65/13    z = 5

Завдання 865

Марк вирішив скласти блоксхему для алгоритму розв’язування рівнянь виду ах = b. Чи правильно він її склав? Ні, неправильно.

 

Завдання 866

1. — Б один; 2. — А жодного; 3. — Г безліч.

 

Завдання 867

а) 3(x + 4) + 6(11 – x) = 9    3x + 12 + 66 – 6x = 9     78 – 3x = 9    –3x = 9 – 78    –3x = –69    x = 23	б) 8(1 – x) + 5(x – 2) = 2    8 – 8x + 5x – 10 = 2    –3x – 2 = 2    –3x = 4    x = –4/3 = –1 1/3
в) 7(x – 5) – 3(2x – 6) = 10    7x – 35 – 6x + 18 = 10    x – 17 = 10    x = 27	г) 18 + 3(x – 5) + 8x = 2(5 + 2x)    18 + 3x – 15 + 8x = 10 + 4x    11x + 3 = 10 + 4x    11x – 4x = 10 – 3    7x = 7    x = 1

Завдання 868

а) 7(4 – t) + 3(t – 5) = 9t    28 – 7t + 3t – 15 = 9t    13 – 4t = 9t    –4t – 9t = –13    –13t = –13    t = 1	б) 3(x + 1,5) + 2(3 + x) = –5    3x + 4,5 + 6 + 2x = –5    5x + 10,5 = –5    5x = –5 – 10,5    5x = –15,5    x = –15,5/5    x = –3,1
в) 5(3 – 2x) – (12 – 7x) = 0    15 – 10x – 12 + 7x = 0    3 – 3x = 0    –3x = –3    x = 1	г) 5z + 2(4 + z) = 3z + 28    5z + 8 + 2z = 3z + 28    7z + 8 = 3z + 28    7z – 3z = 28 – 8    4z = 20    z = 5

Завдання 869

а) 3(2x + 3) – 5(7 – 4x) – 2(5x + 4) = –2    6x + 9 – 35 + 20x – 10x – 8 = –2    16x – 34 = –2    16x = 34 – 2    16x = 32     x = 2

б) 8(4 – 3x) + 7(x – 3) + 3(9 + 7x) = 10    32 – 24x + 7x – 21 + 27 + 21x = 10    4x + 38 = 10    4x = –28    x = –7

Завдання 870

а) 6(x + 2) + 3(3x + 7) = 4(5 + 4x) – 7    6x + 12 + 9x + 21 = 20 + 16x – 7    15x + 33 = 16x + 13    15x – 16x = 13 – 33    –x = –20    x = 20

б) 5(12 – x) – 11(4x – 5) = 9(9 – 5x) – 26    60 – 5x – 44x + 55 = 81 – 45x – 26    115 – 49x = 55 – 45x    115 – 55 = 49x – 45x    60 = 4x    x = 15

Завдання 871

а) 1/2x + 1/4(x – 2) = x    2x + x – 2 = 4x    x = –2	б) 1/2(4x – 5) + 3/2(2x + 1) = x + 3    4x – 5 + 6x + 3 = 2x + 6    8x = 8    x = 1
в) 2/3(5 – 3x) + 1/3(2 + 9x) = 2x – 1    10 – 6x + 2 + 9x = 6x – 3    3x = 15    x = 5	г) 2 + 1/4(8x + 1) = 5x + 3/4(4x – 1)    8 + 8x + 1 = 20x + 12x – 3    24x = 12    x = 1/2

Завдання 872

а) 1/2 + 2(1/3 n + 1) = 3n    1/2 + 2/3 n + 2 = 3n    3 + 4n + 12 = 18n    14n = 15     n = 15/14 = 1 1/14

б) 3/5(6 + 7x) – 2x = 2/5(4 + 3x) + 3    18 + 21x – 10x = 8 + 6x + 15    5x = 5    x = 1

Завдання 873

а)	б)
(2x – 3)/3 + (x – 1)/2=(5x – 3)/6 |•6 2(2x – 3) + 3(x – 1) = 5x – 3 4x – 6 + 3x – 3 = 5x – 3 2x = 6 x = 3	(3x + 1)/4 – (2x – 4)/3=3 – (7 – x)/2 |•12 3(3x + 1) – 4(2x – 4) = 36 – 6(7 – x) 9x + 3 – 8x + 16 = 36 – 42 + 6x 5x = 25 x = 5
в)	г)
(2 – 3x)/2 + (6x + 1)/5=(x – 4)/4 |•20 10(2 – 3x) + 4(6x + 1) = 5(x – 4) 20 – 30x + 24x + 4 = 5x – 20 11x = 44 x = 4	(x + 6)/5 – (5 – 2x)/3=2x – (3x – 2)/2 |•30 6(x + 6) – 10(5 – 2x) = 60x – 15(3x – 2) 6x + 36 – 50 + 20x = 60x – 45x + 30 11x = 44 x = 4

Завдання 874

а)	б)
(x + 1)/2 + (3x – 5)/6=(5x – 6)/4 |•12 6(x + 1) + 2(3x – 5) = 3(5x – 6) 6x + 6 + 6x – 10 = 15x – 18 3x = 14 x = 14/3 = 4 2/3	(3x + 1)/5 – (6 – x)/4=3x + (5x + 16)/2 |•20 4(3x + 1) – 5(6 – x) = 60x + 10(5x + 16) 12x + 4 – 30 + 5x = 60x + 50x + 160 93x = –186 x = –2

Завдання 875

Одне число більше за інше на 6. Якщо перше помножити на 5, а друге – на 4, то перший добуток буде більший за другий на 40. Знайдіть ці числа.

Розв'язання

Нехай одне невідоме число – x, тоді друге число (x – 6). Складаємо рівняння:

5x – 4(x – 6) = 40

5x – 4x + 24 = 40

x = 16 – перше невідоме число;

16 – 6 = 10 – друге невідоме число.

Відповідь: 10 і 16.

 

Завдання 876

Одне число більше за інше в 6 разів. Якщо від більшого з них відняти 37, а до меншого додати 73, то результати будуть рівні. Знайди ці числа.

Розв'язання

Нехай одне невідоме число – x, тоді друге 6x. Складаємо рівняння:

6x – 37 = x + 73

5x = 110

x = 22 – перше невідоме число;

6 • 22 = 132 – друге невідоме число.

Відповідь: 22 і 132.

 

Завдання 877

Яке число більше від своєї третьої частини на 1/3

Розв'язання

Нехай x невідоме число. Складаємо рівняння:

x – 1/3x = 1/3

2/3 x = 1/3

2x = 1

x = 1/2 – невідоме число.

Відповідь: 1/2.

 

Завдання 878

а) |x| + 5 = 12    |x| = 12 – 5    |x| = 7    x = 7 або x = –7    Перевірка:    |7| + 5 = 7 + 5 = 12    |–7| + 5 = 7 + 5 = 12	б) 2|x| + 3 = 25    2|x| = 25 – 3    2|x| = 22    |x| = 22 : 2    |x| = 11     x = 11 або x = –11 Перевірка: 2|11| + 3 = 2 • 11 + 3 = 22 + 3 = 25 2|–11| + 3 = 2 • 11 + 3 = 22 + 3 = 25
в) |x – 2| = 12     x – 2 = 12 або x – 2 = –12     x = 14 або x = –10     Перевірка:     |14 – 2| = |12| = 12     |–10 – 2| = |–12| = 12	г) |2x – 3| + 8 = 5    |2x – 3| = 5 – 8    |2x – 3| = –3    Розв’язків немає

Завдання 879

а) |x| – 8 = –3    |x| = –3 + 8    |x| = 5    x = 5 або x = –5    Перевірка:    |5| – 8 = 5 – 8 = –3    |–5| – 8 = 5 – 8 = –3	б) |2x| – 3 = 5     |2x| = 5 + 3     |2x| = 8     2x = 8 або 2x = –8     x = 4 або x = –4     Перевірка:     |2(4)| – 3 = |8| – 3 = 8 – 3 = 5     |2(–4)| – 3 = |8| – 3 = 8 – 3 = 5
в) |x + 4| = 0     x + 4 = 0 або x + 4 = 0     x = –4     Перевірка:     |–4 + 4| = |0| = 0	г) |x – 1| + 7 = 3    |x – 1| = 3 – 7    |x – 1| = –4    Розв’язків немає

Завдання 880

Розв’яжи тільки ті рівняння, які можна звести до лінійних рівнянь.

а) (x² – 2)² – x4 = 0    (x² – 2)² = x4    (x² – 2)(x² – 2) = x4    x4 – 4x² + 4 = x4    –4x² + 4 = 0    4x² = 4    x² = 1    x = 1 або x = –1

б) (x + 2)² – (x + 1)² = 0    (x + 2 + x + 1)(x + 2 – x – 1) = 0    (2x + 3)(1) = 0    2x + 3 = 0    x = –3/2

Завдання 881

Solve only those equations that can be reduced to linear equations.

а) (x² – 4)² – x4 – 8 = 0    (x² – 4)² = x4 + 8     x4 – 8x² + 16 = x4 + 8     –8x² + 16 = 8     –8x² = 8 – 16     –8x² = –8     x² = 1     x = 1 або x = –1

б) (x + 3)² – (x – 3)² = 12     (x + 3 + x – 3)(x + 3 – x + 3) = 12     2x • 6 = 12     12x = 12      x = 1

Завдання 882

а) (а + 3)x = 12     x = 12/(а + 3)     a ≠ –3

б) (а – 6)x = а + 6     x = (а – 6)/(а – 6)     a ≠ 6

в) (а² + 5)x = 2     x = 2/(а² + 5)     а – будь-яке значення

Завдання 883

а) (а – 4)x = 15     x = 15/(а – 4)     a ≠ 4

б) (а + 7)x = а – 7     x = (а – 7)/(а + 7)     a ≠ –7

в) (а² + 2)x = 4     x = 4/(а² + 2)     a – будь-яке значення

Завдання 884

Доведи, що при будь–яких значеннях а рівняння має єдиний корінь.

а) (a² + 3)x = 5; 

x = 5/(a² + 3), де a² + 3 ≠ 0.

Оскільки a² ≥ 0, то a² + 3 > 0 для всіх значень а, тому рівняння має єдиний корінь.

б) (a² + 1)x = a; 

x = a/(a² + 1), де a² + 1 ≠ 0; 

Оскільки a² ≥ 0, то a² + 1 > 0 для всіх значень а, тому рівняння має єдиний корінь.

в) 4 – 5x = a²x; 

4 = x(5 + a²); x = 4/(5 + a²), де 5 + a² ≠ 0.

Оскільки a² ≥ 0, то 5 + a² > 0 для всіх значень а, тому рівняння має єдиний корінь.

 

Завдання 885

а) (a² + 6)x = 5; 

x = 5/(a² + 6), де a² + 6 ≠ 0;

оскільки a² ≥ 0, то a² + 6 > 0 для всіх значень а, тому рівняння має єдиний корінь.

б) (a² + 8)x = a; 

x = a/(a² + 8), де a² + 8 ≠ 0;

оскільки a² ≥ 0, то a² + 8 > 0 для всіх значень а, тому рівняння має єдиний корінь.

в) a²x = –2x + 3; a²x + 2x = 3; x(a² + 2) = 3; 

x = 3/(a² + 2), де a² + 2 ≠ 0;

оскільки a² ≥ 0, то a² + 2 > 0 для всіх значень а, тому рівняння має єдиний корінь.

 

Завдання 886

Для кожного з пунктів а–г визнач, при яких значеннях коефіцієнта k рівняння: 1) має єдиний корінь; 2) не має коренів; 3) має безліч коренів.

а) kx = 8 

1) Має єдиний корінь, якщо k ≠ 0 (x = 8/k). 

2) Не має коренів, якщо k = 0, оскільки 0x = 8 не має розв'язків. 

3) Не має безлічі коренів, оскільки рівняння лінійне і може мати тільки один корінь при k ≠ 0.

б) (k + 3)x = 5 

1) Має єдиний корінь, якщо k + 3 ≠ 0 (x = 5/(k + 3)). 

2) Не має коренів, якщо k + 3 = 0 (x не існує). 

3) Не має безлічі коренів, оскільки рівняння завжди лінійне при k ≠ –3.

в) kx = k 

1) Має єдиний корінь, якщо k ≠ 0 (x = 1). 

2) Не має коренів, якщо k = 0, оскільки 0x = 0 не дає певного розв'язку. 

3) Має безліч коренів, якщо k = 0, оскільки 0x = 0, і x може бути будь–яким числом.

г) (2 – k)x = (2 – k) 

1) Має єдиний корінь, якщо k ≠ 2 (x = 1). 

2) Не має коренів, якщо k = 2 і x ≠ 1. 

3) Має безліч коренів, якщо k = 2, оскільки 0x = 0 має безліч розв'язків.

 

Завдання 887

Для кожного з пунктів а–г визнач, при яких значеннях коефіцієнта т рівняння: 1) має єдиний корінь; 2) не має коренів; 3) має безліч коренів.

а) mx = 12 

1) Має єдиний корінь, якщо m ≠ 0 (x = 12/m). 

2) Не має коренів, якщо m = 0, оскільки 0x = 12 не має розв'язків. 

3) Не має безлічі коренів, оскільки рівняння завжди лінійне і може мати тільки один корінь при m ≠ 0.

б) (m – 5)x = 15 

1) Має єдиний корінь, якщо m – 5 ≠ 0 (x = 15 / (m – 5)). 

2) Не має коренів, якщо m – 5 = 0 (x не існує). 

3) Не має безлічі коренів, оскільки рівняння завжди лінійне при m ≠ 5.

в) mx = 2m 

1) Має єдиний корінь, якщо m ≠ 0 (x = 2). 

2) Не має коренів, якщо m = 0, оскільки 0x = 0 не дає певного розв'язку. 

3) Має безліч коренів, якщо m = 0, оскільки 0x = 0, і x може бути будь–яким числом.

г) (7 + m)x = (7 + m) 

1) Має єдиний корінь, якщо m ≠ –7 (x = 1). 

2) Не має коренів, якщо m = –7 і x ≠ 1. 

3) Має безліч коренів, якщо m = –7, оскільки 0x = 0 має безліч розв'язків. 

 

Завдання 888

Для кожного пункту а–в допишіть після знаку рівності замість крапок вираз.

а) 5x – 4 + 2x = ...;

1) має один корінь: 5x – 4 + 2x = 10 

2) має безліч коренів: 5x – 4 + 2x = 7x – 4 

3) не має коренів: 5x – 4 + 2x = 7x – 5 

б) 2(1,5x – 7) – 3x = ...;

1) має один корінь: 2(1,5x – 7) – 3x = 4 

2) має безліч коренів: 2(1,5x – 7) – 3x = 3x – 14 

3) не має коренів: 2(1,5x – 7) – 3x = –6x + 10 

в) (3x + 2)/5 = … .

1) має один корінь: (3x + 2)/5 = 2 

2) має безліч коренів: (3x + 2)/5 = (3x + 2)/5 

3) не має коренів: (3x + 2)/5 = 3x + 5 

 

ЦІКАВІ ЗАДАЧІ

Завдання 889

Задача з болгарського фольклору. На запитання, яка маса його риби, рибалка відповів: «Хвіст має масу 150 г, голова – стільки, скільки хвіст і половина тулуба, а тулуб – скільки голова і хвіст разом». Яка маса риби?

Розв'язання

Нехай половина тулуба риби важить х кг, тоді увесь тулуб важить 2х г, а голова (150 + х) г. Голова і хвіст разом важать (150 + х) + 150 = (х + 300) г, що дорівнює масі тулуба 2х г. Складемо рівняння:

2х = 300 + х

2х – х = 300

х = 300

150 + 300 = 450 (г) – важить голова;

300 • 2 = 600 (г) – важить тулуб;

450 + 600 + 150 = 1200 (г) = 1 кг 200 г – маса усієї риби.

Відповідь: 1 кг 200 г.

 

Завдання 890

Значення виразу 3(x + a)/2 + 0,5x + 3 дорівнює 4, якщо x = –1. Чому дорівнює значення виразу, якщо x = 5?

3(–1 + a)/2 + 0,5 • (–1) + 3 = 4   |•2

3(–1 + a) + 0,5 • (–1) • 2 + 3 • 2 = 4 • 2

3(–1 + a) – 1 + 6 = 8 

–3 + 3a + 5 = 8

3a + 2 = 8

3a = 6

a = 2

3(5 + 2)/2 + 0,5 • 5 + 3 = 3 • 7/2 + 2,5 + 3 =21/2 + 2,5 + 3 = 10,5 + 5,5 = 16

 

ВПРАВИ ДЛЯ ПОВТОРЕННЯ

Завдання 891

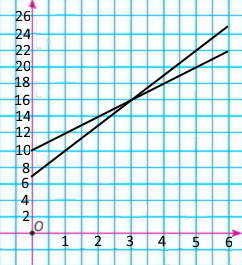
Перебуваючи за кордоном, ти маєш можливість користуватися послугами одного з двох мобільних операторів. Перший пропонує сплачувати 10 грн за першу хвилину і 2 грн за кожну наступну хвилину розмов, а другий – 7 грн і 3 грн відповідно. Побудуй графік залежності вартості розмови від часу, що не перевищує 6 хв, для кожного оператора. Який висновок можна зробити?

Вартість розмови до трьох хвилин включно дешевша в другого оператора

Вартість розмови, починаючи з четвертої хвилини дешевша в першого оператора.

 

Завдання 892

а) 5a³, якщо a = 0,2: 

5 • (0,2)³ = 5 • 0,008 = 0,04

б) 2x² – x⁴ – 5 = x²(2 – x²) – 5, якщо x = –2:
(–2)²(2 – (–2)²) – 5 = 4(2 – 4) – 5 = –13

в) a³ + 3a² = a²(a + 3), якщо a = 0,2:
(0,2)²(0,2 + 3) = 0,04 • 3,2 = 0,128

г) 3a⁴ – a² = a²(3a² – 1), якщо a = –1,2:
(–1,2)²(3(–1,2)² – 1) = 1,44 • (4,32 – 1) = 1, 44 • 3,32 = 4,7808

 

Завідання 893

а) 20% від 350 — це 0,20 • 350 = 70

б) 30% від 56 000 — це 0,30 • 56 000 = 16 800
в) 12% від 0,75 — це 0,12 • 0,75 = 0,09
г) 125% від 1,4 — це 1,25 • 1,4 = 1,75

Інші завдання дивись тут...