Завдання 949 Рівняння з двома змінними
|
а) 3x – у = 5 Лінійне рівняння в) xy – 28 = 3 |
б) x3 + 4z = 9 д) x – 2(3 – у) = 5 |
Завдання 950 Кілька розв’язків рівняння
а) x + у = 5; (–1;6), (5;0), (1;4), (2;3), (0;5), (3;2)
б) x – у = 2; (–2;–4), (–1;–3), (8; 6), (4; 2), (1;–1)
в) xy = 30. (5;6), (6;5), (15;2), (2;15), (1;30 ), (30;1)
Завдання 951
Чи має розв’язки рівняння?
а) x² + у² = –3; Рівняння не має розв'язків, бо x² + у² ≥ 0
б) |х| + |у| = 0; Рівняння має розв'язки, якщо x = 0 і y = 0
в) x4 + |у| = –8. Рівняння не має роззв'язків, бо x4 + |у| ≥ 0
Завдання 952
Значення x = 5 і у = –2 не задовільняють рівняння 5x – 2у = 10.
5 • 5 – 2 • (–2) = 25 + 4 = 29
Завдання 953
Пара (2;–1) є розв'язком 2х – 5у = 9, бо 2 • 2 – 5 • (–1) = 4 + 5 = 9, тому Г (2;–1)
Завдання 954
а) 2x + 7у = 20; пара (3;2) є розв’язком рівняння, бо 2 • 3 + 7 • 2 = 20
б) –2t + 3z = 10; пара (1;4) є розв’язком рівняння –2 • 1 + 3 • 4 = 10
в) x – 4у = 16. пара (4;–3) є розв’язком рівняння 4 – 4 • (–3) = 16
Завдання 955
а) х + у = 0; пара (–1;1) є розв’язком рівняння, бо –1 + 1 = 0
б) 5x – у = 3; пара (1;2) є розв’язком рівняння, бо 5 • 1 – 2 = 3
в) 2х + 3у = 1. пара (–1;1) є розв’язком рівняння, бо 2 • (–1) + 3 • 1 = 1
Завдання 956 Будь–які три розв’язки рівняння
а) x – у = 16; (0;–16), (16;0), (17;1)
б) 2x + у = 3,5; (–1;5,5), (1;1,5), (3;–2,5)
в) 4a + 5b = 20. (5;0), (0;4), (2,5;2)
Завдання 957 Будь–які два розв’язки рівняння
а) 2x + у = 7; (3;1), (8;–9)
b) 2x – 3z = 10; (5;0), (2;–2)
c) 4x + 5n = 21. (–1;5), (4;1)
Завдання 959
Рівняння x + 3у = 10 задовільняють пари чисел (1;3), (4;2), (–2;4), (4;2), (10;0), (25;–5)
Завдання 960
Рівняння 5x + у = 12 задовільняють пари чисел (1;7), (3;–3), (–4;32), (2;2), (3;–3), (2,4;0)
Завдання 961
Склади рівняння з двома змінними, розв’язком якого є пара чисел:
|
а) (3;2); 2x + y = 8 |
б) (–2;5); x – 3y = –17 |
в) (1/2;2/5). 2x + 5y = 3 |
Завдання 962
|
а) (1;4); x – 2y = –7 |
б) (–2;3); 2x + y = –1 |
в) (–4,2;–1,5). 5x – 8y = –9 |
Завдання 963
|
а) x – у = 2 1) x = 2 + y 2) y = x – 2 |
б) 5x + у = 15 1) x = (15 – y)/5 2) y = 15 – 5x |
в) x – 2у = 6 1) x = 6 + 2y 2) y = (x – 6)/2 |
Завдання 964
|
а) x – у = 7 1) x = 7 + y 2) y = x – 7 |
б) x + 3у = 12 1) x = 12 – 3y 2) y = (12 – x)/3 |
в) x – 2у = 6 1) x = 6 + 2y 2) y = (x – 6)/2 |
Завдання 965
Знайдіть таке число c, щоб пара (c;–c) задовольняла рівняння.
|
а) 2x + 3у = 20 2c – 3c = 20 –c = 20 c = –20 |
б) 5x – у = 12 5c + c = 12 6c = 12 c = 2 |
в) x – 8у = 9 c + 8c = 9 9c = 9 c = 1 |
г) 7x – 3у = 20 7c + 3c = 20 10c = 20 c = 2 |
Завдання 966
Знайди таке число n, щоб пара (n; –n) задовольняла рівняння.
|
а) 5x + 4у = 3 5n – 4n = 3 n = 3 |
б) 9x² – у = 0 9n² + n = 0 n(9n + 1) = 0 n = 0 або 9n + 1 = 0 n = 0 або n = –1/9 |
в) x² + 4у = 0 n² – 4n = 0 n(n – 4) = 0 n = 0 або n = 4 |
г) x + |у| = 4 n + |–n| = 4 n + n = 4 2n = 4 n = 2 |
Завдання 967
Знайди значення коефіцієнта а в рівнянні ax + 5у = 1, якщо відомо, що пара x = 3, у = –4 є розв’язком цього рівняння.
3a + 5 • (–4) = 1
3a – 20 = 1
3a = 21
a = 7
Завдання 968
Знайди значення коефіцієнта k в рівнянні 3x + kу = 14, якщо відомо, що пара (–2; 5) є розв’язком цього рівняння.
3 • (–2) + 5k = 14
–6 + 5k = 14
5k = 20
k = 4
Завдання 969
Знайди значення коефіцієнта а в рівнянні 5x – ау = 2, якщо його задовольняє пара чисел:
|
а) 5 • 2 – a = 2 10 – a = 2 a = 8 |
б) 5 • 1 – 2a = 2 5 – 2a = 2 2a = 3 a = 1,5 |
в) 5 • 4 – 3a = 2 20 – 3a = 2 3a = 18 a = 6 |
г) 5 • (–5) – 9a = 2 –25 – 9a = 2 9a = –27 a = –3 |
Завдання 970
Доведіть, що рівняння x² + у² = –5 не має розв’язків.
x² ≥ 0 та у² ≥ 0, сума x² + у² ≥ 0 і не може рівняння дорівнювати –5.
Завдання 971
Чи має розв’язки рівняння з двома змінними?
а) x² + у² = –1;
Не має розв'язку, бо x² ≥ 0 та у² ≥ 0, x² + у² ≥ 0 і не може рівняння дорівнювати –1.
б) x² – у² = –3;
Рівняння має розв’язок при y > x.
в) x² + 3у² = 0.
Рівняння має розв’язок при x = 0 та y = 0.
Завдання 972
Доведи, що рівняння не має розв’язків.
а) x² + (у – 1)² = –3;
x² ≥ 0 та (у – 1)² ≥ 0, сума x² + (у – 1)² ≥ 0 і тому не може рівняння дорівнювати –3
б) x² + у² + 2 = 2у;
x² + y² – 2y + 1 + 1 = 0; x² + (y – 1)² = –1. Оскільки x² ≥ 0 та (у – 1)² ≥ 0, сума
x² + (у – 1)² ≥ 0, тому не може рівняння дорівнювати –1
в) |x| + у² +1 = 0.
|x| ≥ 0 та у² ≥ 0, а отже |x| + у² + 1 ≥ 1, тому не може рівняння дорівнювати 0
Завдання 973 Розв'язок рівняння
|
а) x² + (у – 1)² = 0 x² = 0 і (у – 1)² = 0 x = 0 і y = 1 (0;1) |
б) (x + 3)² + у² = 0 (x + 3)² = 0 і у² = 0 x = –3 і y = 0 (–3;0) |
в) (2x + 3)4 + у2 = 0 (2x + 3)4 = 0, у² = 0 2x + 3 = 0 і y = 0 x = –3/2 і y = 0 (–3/2;0) |
Завдання 974
|
а) x² + (у – 2)² = 0 x² = 0 і (y – 2)² = 0 x = 0 і y = 2 (0;2) |
б) (x – 3)2 + (у + 1)4 = 0 (x – 3)2 = 0 і (у + 1)4 = 0 x = 3 і y = –1 (3;–1) |
в) |x| + у² = 0 |x| = 0 і у² = 0 x = 0 і y = 0 (0;0) |
Завдання 975
|
а) x² + у² + 1 = 2x x² – 2x + 1 + y² = 0 (x – 1)² + y² = 0 (x – 1)² = 0 і y² = 0 x = 1 і y = 0 (1;0) |
в) x² + 4у² + 1 = 4у x² + 4y² – 4y + 1 = 0 x² + (2y – 1)² = 0 x² = 0 і (2y – 1)² = 0 x = 0 і y = 1/2 (0;1/2) |
|
б) x² + у² + 9 = 6x x² – 6x + 9 + y² = 0 (x – 3)² + y² = 0 (x – 3)² = 0 і y² = 0 x = 3 і y = 0 (3;0) |
г) 4x² + у² + 2 = 2(2x – у) 4x² + y² + 2 = 4x – 2y 4x² – 4x + 1 + y² + 2y + 1 = 0 (2x – 1)² + (y + 1)² = 0 (2x – 1)² = 0 і (y + 1)² = 0 x = 1/2 і y = –1 (1/2;–1) |
Завдання 976
|
а) x² + у² + 4 = –4x x² + y² + 4 + 4x = 0 x² + 4x + 4 + y² = 0 (x + 2)² + y² = 0 (x + 2)² = 0 і y² = 0 x = –2 і y = 0 (–2;0) |
б) x² + у² + 16 = 8у x² + y² – 8y + 16 = 0 x² + (y – 4)² = 0 x² = 0 і (y – 4)² = 0 x = 0 і y = 4 (0;4) |
|
в) x² + 2x + у² + 5 = 4у x² + 2x + y² – 4y + 4 = 0 (x + 1)² + (y – 2)² = 0 (x + 1)² = 0 і (y – 2)² = 0 x = –1 і y = 2 (–1;2) |
г) x² + у² + 8 = 4(у – x) x² + y² + 8 – 4y – 4x x² + 4x + 4 + y² – 4y + 4 = 0 (x + 2)² + (y – 2)² = 0 (x + 2)² = 0 і (y – 2)² = 0 x = –2 і y = 2 (–2;2) |
Завдання 977
При яких значеннях n рівняння має тільки один розв’язок
а) x² + у² = n, рівняння має тільки один розв’язок (0;0), якщо n = 0
б) x² + |у| = n – 1, рівняння має тільки один розв’язок (0;0), якщо n = 1
Завдання 978
а) |x| + |у| = n + 2, рівняння має тільки один розв’язок (0;0), якщо n = –2
б) (x – 3)4 + у4 = n4, рівняння має тільки один розв’язок (3;0), якщо n = 0
Завдання 979
Установи відповідність між рівняннями (1–3) та кількістю їх розв’язків (А–Г).
1 – А; 2 – В; 3 – Г.
Завдання 980
Знайди натуральні значення x і у, які задовольняють рівняння:
а) x + 4у = 13; (9;1), (5;2), (1;3)
б) 5x + у = 14; (1;9), (2;4)
в) 3x + 2у = 22. (2;8), (4;5), (6;2)
Завдання 981
а) x + 12у = 37; (25;1), (13;2), (1;3)
б) 3x + у = 16; (1;13), (2;10), (3;7), (4;4), (5;1)
в) 4x + 5у = 29. (1;5), (6;1)
Завдання 982
|
а) x² + у² = 2; (1;1) |
б) 2x² + у² = 9. (2;1), (0;3) |
Завдання 983
|
а) x² + у² = 5; (2;1) |
б) x² + 3у² = 31. (2;3) |
Завдання 984
Знайди таке значення a, щоб рівняння 3x – 2у² = 6 мало розв’язок.
|
а) 3a – 2 • 3² = 6 3a – 18 = 6 3a = 24 a = 8 |
б) 3 • 2 – 2a² = 6 6 – 2a² = 6 2a² = 0 a = 0 |
в) 3a – 2 • 0² = 6 3a = 6 a = 2 |
г) 3 • 8 – 2a² = 6 24 – 2a² = 6 2a² = 18 a² = 9 a = 3 або a = –3 |
Завдання 985
Знайдіть двоцифрове число, яке більше за суму його цифр у:
|
а) 2 рази; 10a + b = 2(a + b) 10a + b = 2a + 2b 8a = b a = b/8 b = 0 і а = 0; b = 8 і a = 1. (0;0) не підходить. Невідоме число: 18 |
б) 6 разів; 10a + b = 6(a + b) 10a + b = 6a + 6b 4a = 5b a = 5b/4 b = 4, тоді a = 5; b = 8, тоді a = 10. (10;8) не підходить. Невідоме число: 54 |
в) 4 рази. 10a + b = 4(a + b) 10a + b = 4a + 4b 6a = 3b a = 3b/6 b = 8 і а = 4; b = 6 і a = 3; b = 4 і a = 2; b = 2 іі a = 1. Невідомі числа: 12; 24; 36; 48 |
Завдання 986
Знайди двоцифрове число, яке більше за суму його цифр у:
|
а) 3 рази; 10a + b = 3(a + b) 10a + b = 3a + 3b 7a = 2b a = 2b/7 b = 7 і a = 2. Невідоме число: 27 |
б) 5 разів; 10a + b = 5(a + b) 10a + b = 5a + 5b 5a = 4b a = 4b/5 b = 5 і a = 4. Невідоме число: 45 |
в) 8 разів. 10a + b = 8(a + b) 10a + b = 8a + 8b 2a = 7b a = 7b/2 b = 2 і a = 7; b = 4 і a = 14; b = 6 і a = 21; b = 8 і a = 28. (7;2) підходить. Невідоме число: 72 |
Завдання 987
Знайди двоцифрове число, яке у 2,5 рази більше за добуток його цифр.
10а + b = 2,5аb
20а + 2b = 5ab
Оскільки 5аb і 20а діляться на 5, тоді 2b повинно ділитися на 5, тоді b = 5.
10а + 5 = 2,5 • 5а; 10а + 5 = 12,5а; 2,5а = 5; а = 2.
Відповідь: 25.
Завдання 988
Знайди двоцифрове число, яке в 2 рази більше за добуток його цифр.
10а + b = 2аb;
Оскільки 2аb і 10а діляться на 2, отже b повинно ділитися на 2, тоді b може приймати натуральні значення 2; 4; 6; 8.
Якщо b = 2, 4, 6, 8, то a набуває відповідно значення –1/3, –2, 3, 1 2/3.
Умову задачі задовольняє лише значення а, яке дорівнює 3, тоді b = 6.
Відповідь: 36.
Завдання 989
Є труби завдовжки 7 м і 8 м. Скільки треба взяти таких труб, щоб прокласти трубопровід завдовжки 67 м?
Нехай довжиною 7 м було х труб, а довжиною 8 м було у штук. Складаємо рівняння:
7x + 8y = 67
Значення y не може бути більше 8, бо 7 • 1 + 8 • 8 > 67, тому змінна y може приймати натуральні значення від 1 до 7.
Якщо y = 1, 2, 3, 4, 5, 6, 7, то відповідно х = 8 3/7; 7 2/7; 6 1/7; 5; 3 6/7; 8 3/7; 1 4/7.
Умову задачі задовольняє значення х, яке дорівнює 5, тоді у = 4, тому маємо
5 • 7 + 4 • 8 = 67
Відповідь: треба взяти 5 труб довжиною 7 м і 4 труби довжиною 8 м, щоб прокласти трубопровід завдовжки 67 м.
Завдання 990
Хлопчик має монети вартістю 2 грн і 5 грн. Як він може без решти заплатити 37 грн?
Нехай вартістю 2 грн було х монет, а вартістю 5 грн — у монет. Складаємо рівняння.
2х + 5y = 37
5y = 37 – 2x
y = (37 – 2x)/5, причому х ≤ 16, бо якщо х > 16, тоді 2х + 5y > 37.
37 – 2х — кратне 5, тому 5; 10; 15; 20; 25; 30; 35, тоді х буде
дорівнюватиме відповідно 16; 13,5; 11; 8,5; 6; 3,5; 1.
Умову задачі задовольняють значення х, які дорівнюють 16; 11; 6; 1, тоді y = 1; 3; 5; 7.
Отже, 37 = 16 • 2 + 1 • 5 = 11 • 2 + 3 • 5 = 6 • 2 + 5 • 5 = 1 • 2 + 7 • 5.
Відповідь: без решти заплатити 37 грн хлопчик може так: 16 монет по 2 грн і 1 монета по 5 грн, 11 монет по 2 грн і 3 монети по 5 грн,
6 монет по 2 грн і 5 монет по 5 грн, 1 монета по 2 грн і 7 монет по 5 грн.
Завдання 991
Цукерки розфасовано в коробки по 200 г і 300 г. Скільки і яких треба взяти таких коробок, щоб було 3 кг цукерок?
Нехай по 200 г було х коробок, а по 300 г — у коробок. Складаємо рівняння.
200x + 300y = 3000
2х + 3y = 30
x = (30 – 3y)/2, причому х < 15 і y < 10,
3y — кратне 2, отже, 3y = 6; 3y = 12; 3y = 18; 3y = 24.
y = 2, y = 4, y = 6, y = 8, тоді x = 12, x = 9, x = 6, x = 3.
Отже, 30 000 = 12 • 200 + 2 • 300 = 9 • 200 + 4 • 300 = 6 • 200 + 6 • 300 = 3 • 200 + 8 • 300.
Відповідь: 12 коробок по 200 г і 2 коробки по 300 г, 9 коробок по 200 г і 4 коробки по 300 г, 6 коробок по 200 г і 6 коробок по 300 г, 3 коробки по 200 г і 8 коробок по 300 г.
Завдання 992
Якщо деяке двоцифрове число помножити на суму його цифр, то вийде 370. Знайди це число.
(10а + b)(а + b) = 370
Оскільки 370 = 37 • 2 • 5 і число 37 — просте, то 10а + b = 37, а + b = 10
Відповідь: 37.
Завдання 993
Склади таке рівняння зі змінними x і у, щоб його задовольняли дві пари чисел.
|
а) (–2;6) і (0;0); 3x + y = 0 б) (5;0) і (–1;–3); –x + 2y = 5 |
в) (–3;2) і (0;–4); 2x + y = –4 г) (2;1) і (1;–1). –2x + y = –3 |
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 994
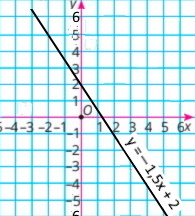
Побудуй графік функції у = –1,5x + 2
|
х |
0 |
2 |
|
у |
2 | –1 |
Завдання 995
Доведи тотожність двома способами.
а) 4a4 + 1 = (2a2 – 2a + 1)(2a2 + 2a + 1);
1 спосіб
4а4 + 1 = 4а4 + 4а2 + 1 – 4а2 = (1 + 2a²)² – (2a)² = (1 + 2a² – 2a)(1 + 2a² + 2a) =
= (2a² – 2a + 1)(2a² + 2a + 1). Тотожній доведено;
2 спосіб
(2a² – 2a + 1)(2a² + 2a + 1) = (2a² + 1)² – (2a²) = 4а4 + 4а2 + 1 – 4а2 = 4а4 + 1.
Тотожність доведено.
б) a4 + a2 + 1 = (a² – a + 1)(a² + a + 1).
1 спосіб
а4 + а² + 1 = а4 + 2а² + 1 – a² = (а² + 1)² – а² = (а4 + 1 – а)(а² + 1 + а). Тотожність
доведено;
2 спосіб
(а² – a + 1)(а² +а + 1) = (а² + 1)² – a² = a4 + 2a² + 1 – a² = a4 + a² + 1. Тотожність
доведено.
Завдання 996
За якої умови рівняння (a – 1)x = 3a – 3 має безліч розв’язків?
(а – 1)х = 3(а – 1) має безліч розв’язків, якщо а – 1 = 0, тобто а = 1.
Відповідь: a = 1.