Інші завдання дивись тут...

Завдання 997

Скільки розв’язків має рівняння?

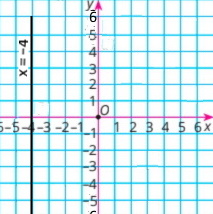
а) 0x + 0у = 20; жодного г) 9x + 0у = 18; безліч

б) 0x + 0у = 0; безліч ґ) x + у = 0; безліч

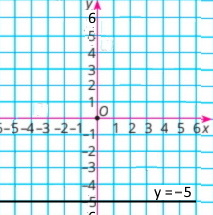
в) 0x + 2у = 0; безліч д) x – у = 1. безліч

Завдання 998

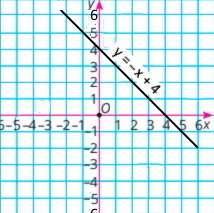
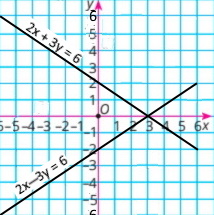
Графіком якої функції є графік рівняння 2x + у = 8? Б у = –2х + 8

 

Завдання 999

Чи відрізняється графік функції у = 0,5x – 2 від графіка рівняння x – 2у = 4?

Графіки співпадають, бо рівняння графіків рівносильні.

 

Завдання 1000

Чи проходить через початок координат графік рівняння?

а) 3x – 2у = 0; Так, бо 3 • 0 – 2 • 0 = 0;

б) 2x – 3у = 7; Ні, бо 2 • 0 – 3 • 0 = 0, 0 ≠ 7;

в) 3(x – 4) = 4(у – 3). Так, бо 3(0 – 4) = 4(0 – 3), –12 = –12.

 

Завдання 1001

Яка з точок не належить графіку рівняння х – 3у = 5?

Точка А(5;0) належить графіку, бо 5 – 3 • 0 = 5

Точка Б (8;1) належить графіку, бо 8 – 3 • 1 = 5

Точка В (–1;–2) належить графіку, бо –1 – 3 • (–2) = 5

Точка Г (4;–3) не належить графіку, бо 4 – 3 • (–3) = 13

 

Завдання 1002

Точка з абсцисою 2 належить графіку рівняння 7x – 2у = 12. Знайди ординату цієї точки.

Якщо х = 2, то 7 • 2 – 2y = 12; 14 – 2y = 12; 2y = 2; y = 1

 

Завдання 1003

Точка з ординатою 1,5 належить графіку рівняння 5x + 4у = 16. Знайди абсцису цієї точки.

Якщо у = 1,5, то 5x + 4 • 1,5 = 16; 5x + 6 = 16; 5x = 10; x = 2

 

Завдання 1004

Чи належить точка A(–3;2) графіку рівняння?

а) 5x + 12у = 9; Належить, бо 5 • (–3) + 12 • 2 = –15 + 24 = 9

б) 2x + 3y = x; Не належить, бо 2 • (–3) + 3 • 2 = –6 + 6 = 0; 0 ≠ –3

в) 5(x + 3) = 4(у – 2). Належить, бо 5 • (–3 + 3) = 4 • (2 – 2), 0 = 0

 

Завдання 1005

Чи належить точка М(2;–1) графіку рівняння?

а) 3x + 5у = 1; Належить, бо 3 • 2 + 5 • (–1) = 6 – 5 = 1

б) 3x + 7у = у; Належить, бо 3 • 2 + 7 • (–1) = 6 – 7 = –1;

в) 2(x – 2) = 4(у – 1). Не належить, бо 2 • (2 – 2) = 4 • (–1 – 1), 0 ≠ –8 

 

Завдання 1006

Виразіть з даного рівняння змінну у через змінну х і знайдіть два розв’язки рівняння.

а) x + у = 7    y = 7 – x Якщо х = 0, то у = 7 Якщо х = 1, то у = 6    (0;7) і (1;6)

б) 2x + у = 5     y = 5 – 2x Якщо х = 0, то у = 5 Якщо х = 1, то у = 3     (0;5) і (2;1)

в) 4x + 3у = 12     y = (12 – 4x)/3     y = 4 – 4/3 x Якщо х = 0, то у = 4 Якщо х = 3, то у = 0      (0;4) і (3;0)

Завдання 1007

Вирази з даного рівняння змінну х через змінну у і знайди два розв’язки рівняння.

а) x – у = 4     x = y + 4 Якщо у = 0, то х = 4 Якщо у = 1, то х = 5   (4;0) і (5;1)

б) x + 3у = 6    x = 6 – 3y Якщо у = 0, то х = 6 Якщо у = 1, то х = 3     (6;0) і (3;1)

в) в) 2x + 5у = 10        x = (10 – 5y)/2        х = 5 – 5/2 у Якщо у = 0, то х = 5 Якщо у = 2, то х = 0     (5;0) і (0;2)

Завдання 1008

Знайди п’ять розв’язків рівняння 3x + 4у = 8.

Усі точки розміщені на прямій.

4у = 8 – 3x

у = (8 – 3x)/4

у = 2 – 3/4 x

Якщо x = 0, то у = 2 – 3/4 • 0 = 2; 

якщо x = 4, то у = 2 – 3/4 • 4 = 2 – 3 = –1;

якщо x = 8, то у = 2 – 3/4 • 8 = 2 – 6 = –4;

якщо x = –4, то у = 2 – 3/4 • (–4) = 2 + 3 = 5;

якщо x = –8, то у = 2 – 3/4 • (–8) = 2 + 6 = 8.

Відповідь: (0;2), (4;–1), (8;–4), (–4;5), (–8;8).

 

Завдання 1009

Знайди чотири розв’язки рівняння 2x – 3у = 6.

Усі точки розміщені на прямій.

–3у = 6 – 2x
у = (2x – 6)/3

у = 2/3 х – 2

Якщо x = 0, то у = 2/3 •  0 – 2 = –2;

якщо x = 3, то у = 2/3 •  3 – 2 = 0;

якщо x = 6, то у = 2/3 •  6 – 2 = 4 – 2 = 2;

якщо x = –3, то у = 2/3 •  (–3) – 2 = –2 – 2 = –4.

Відповідь: (0;–2), (3;0), (6;2), (–3;–4).

 

Завдання 1010 Побудуй графік рівняння

а) x + у = 4	б) 2x + у = 6	в) 3x + 2у = 0
х 0 4 у 4 0	х 0 1 у 6 4	х 0 4 у 0 –6

Завдання 1011 Graph the equation.

а) 2x + у = 5	б) 3x – 2у = 3	в) x + 3у = 0
х 0 1 у 5 3	х 0 1 у 1,5 3	х 0 6 у 0 –2

Завдання 1012

На графіку рівняння 0,6x + у = 2,2 взято точку. Яка ордината цієї точки, якщо її абсциса дорівнює:

а) –8	б) –3	в) 2	г) 7
0,6 • (–8) + у = 2,2 –4,8 + у = 2,2 у = 2,2 + 4,8 у = 7	0,6 • (–3) + у = 2,2 –1,8 + у = 2,2 у = 2,2 + 1,8 у = 4	0,6 • 2 + у = 2,2 1,2 + у = 2,2 у = 2,2 – 1,2 у = 1	0,6 • 7 + у = 2,2 4,2 + у = 2,2 у = 2,2 – 4,2 у = –2

Завдання 1013

Знайди абсцису точки, взятої на прямій, що є графіком рівняння 11x – 4у = 80, якщо її ордината дорівнює:

а) –31	б) –20	в) –3,5	г) 2
11x – 4 • (–31) = 80 11x + 124 = 80 11x = 80 – 124 11x = –44 x = –44 : 11 x = –4	11x – 4 • (–20) = 80 11x + 80 = 80 11x = 80 – 80 11x = 0 x = 0	11x – 4 • (–3,5) = 80 11x + 14 = 80 11x = 80 – 14 11x = 66 x = 66 : 11 x = 6	11x – 4 • 2 = 80 11x – 8 = 80 11x = 80 + 8 11x = 88 x = 88 : 11 x = 8

Завдання 1014

Графік рівняння 2x + 5у = c проходить через задані точки. Установи відповідність між точками, заданими умовами (1–4), та значенням с (А–Д), яке відповідає цим умовам.

 Відповідь: 1 — Г; 2 — В; 3 — Д; 4 — Б

 

Завдання 1015

Яким має бути коефіцієнт a рівняння ax – 4у = 12, щоб графік цього рівняння проходив через точку:

а) M(10;2)	б) N(–1;–1)	в) P(2;–3)	г)  Q(6;6)
a • 10 – 4 • 2=12 10a – 8 = 12 10a = 20 а = 20 : 10 a = 2	a • (–1) – 4 • (–1)=12 –a + 4 = 12 –a = 12 – 4 –а = 8 a = –8	11x – 4 • (–3,5)=80 a • 2 – 4 • (–3)=12 2a + 12 = 12 2a = 0 a = 0	a • 6 – 4 • 6=12 6a – 24 = 12 6a = 36 а = 36 : 6 a = 6

Завдання 1016

При якому значенні b графік рівняння 6x + by = 0 проходить через точку?

а) N(2;3)	б) O(0;0)	в) P(–4;8)	г)  R(–3;–2)
6 • 2 + b • 3 = 0 12 + 3b = 0 3b = –12 b = –12 : 3 b = –4	6 • 0 + b • 0 = 0 b • 0 = 0 b — будь–яке	6 • (–4) + b • 8 = 0 –24 + 8b = 0 8b = 24 b = 24 : 8 b = 3	6 • (–3) + b • (–2) = 0 –18 – 2b = 0 –2b = 18 b = 18 : (–2) b = –9

Завдання 1017

За якої умови графік функції у = 1,5x + c є графіком рівняння 3x – 2у = 4?

у = 1,5x + c

1,5x – y = –c   |•2

3x – 2y = –c і 3x – 2y = 4

–c = 4 

Графіки співпадають при c = –4. 

 

Завдання 1018

Не виконуючи побудови, знайди координати точок перетину з осями координат.

а) 3x + 2у = 6 З віссю Оу (х = 0) 3 • 0 + 2y = 6 2y = 6 y = 3 Точка (0;3) З віссю Ох (у = 0) 3x + 2 • 0 = 6 3x = 6 x = 2 Точка (2;0)

б) x + 5у = 10 З віссю Оу (х = 0) 0 + 5y = 10 5y = 10 y = 2 Точка (0;2) З віссю Ох (у = 0) x + 5 • 0 = 10 x = 10 Точка (10;0)

в) 3x + 4у = 24 З віссю Оу (х = 0) 3 • 0 + 4y = 24 4y = 24 y = 6 Точка (0;6) З віссю Ох (у = 0) 3x + 4 • 0 = 24 3x = 24 x = 8 Точка (8;0)

Завдання 1019

а) 2x – 7у = 14 З віссю Оу (х = 0) 2 • 0 – 7y = 14 –7y = 14 y = –2 Точка (0;–2) З віссю Ох (у = 0) 2x – 7 • 0 = 14 2x = 14 x = 7 Точка (7;0)

б) –x + 2у = 4 З віссю Оу (х = 0) –0 + 2y = 4 2y = 4 y = 2 Точка (0;2) З віссю Ох (у = 0) –x + 2 • 0 = 4 –x = 4 x = –4 Точка (–4;0)

в) 5x – 6у = 30 З віссю Оу (х = 0) 5 • 0 – 6y = 30 –6y = 30 y = –5 Точка (0;–5) З віссю Ох (у = 0) 5x – 6 • 0 = 30 5x = 30 x = 6 Точка (6;0)

Завдання 1020, 1021

Побудуй в одній координатній площині графіки рівнянь.

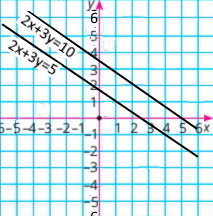
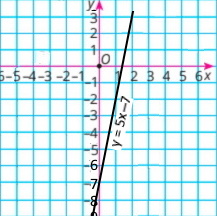
2x + 3у = 5	2x + 3у = 10	5x – у = 7	10x – 2у = 14
х 0 1 у 5/3 1	х 0 4 у 10/3 2	х 0 2 у –7 3	х 0 2 у –7 3

Завдання 1022

Не виконуючи побудову, установи взаємне розміщення графіків рівнянь.

а) 2x – 9у = 18 і 3x – 5у = 15; 2/3 ≠ (–9)/(–5) — прямі перетинаються

б) 2x – 9у = 18 і 4x – 18у = 20; 2/4 = (–9)/(–18) ≠ 18/20 — прямі паралельні

в) 3x – 5у = 15 і 9x – 15у = 45; 3/9 = (–5)/(–15) = 15/45 — прямі збігаються

 

Завдання 1023

а) 3x + 2у = 6 і 2x + 4у = 11; 3/2 ≠ 2/4 — прямі перетинаються

б) 3x + 2у = 6 і 6x + 4у = 12; 3/6 = 2/4 = 6/12 — прямі збігаються

в) 2x – 7у = 1 і 6x – 21у = 5; 2/6 = (–7)/(–21) ≠ 1/5 — прямі паралельні

Завдання 1024

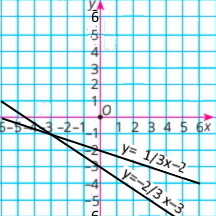
Побудуй в одній координатній площині графіки рівнянь та знайди координати точки їх перетину.

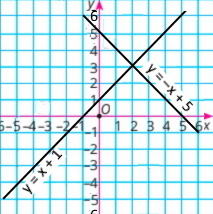
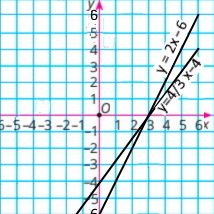
а) x + у = 5 і x – у = –1		б) 2x – у = 6 і 4x – 3у = 12
у = 5 – х х 0 5 у 5 0	у = х + 1 х 0 3 у 1 3	у = 2х – 6 х 0 2 у –6 –2	у = 4/3 х – 4 х 0 3 у –4 0
Координати точки перетину (2;3)		Координати точки перетину (3;0)

Завдання 1025

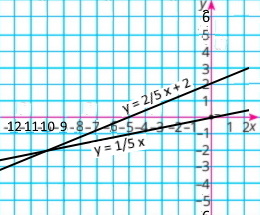
а) 2x + 3у = –9 і x + 3у = –6		б) x – 5у = 0 і 2x – 5у = –10
у = –2/3 х –3  х 0 3 у –3 –5	у = –1/3 х –2 х 0 3 у –2 –3	у = 1/5 х х –5 5 у –1 1	у = 2/5 х + 2 х 0 5 у 2 4
Координати точки перетину (–3;–1)		Координати точки перетину (–10;–2)

Завдання 1026

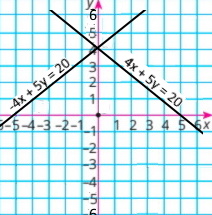
Установи взаємне розміщення графіків рівнянь та побудуй в одній координатній площині графіки цих рівнянь.

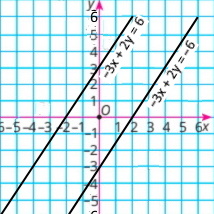
а) 4x + 5у = 20 і –4x + 5у = 20 4/(–4) ≠ 5/5 Прямі перетинаються	б) –3x + 2у = 6 і –3x + 2у = –6 (–3)/(–3) = 2/2 ≠ 6/(–6) Прямі паралельні

Завдання 1027

а) 2x + 3у = 6 і 2x – 3у = 6 2/2 ≠ 3/(–3) Прямі перетинаються	б) 5x – 2у = 10 і 10x – 4у = 20 5/10 = (–2)/(–4) = 10/20 Прямі збігаються

Завдання 1028

а) 0x + 5у = 10	б) 3x + 0у = 9
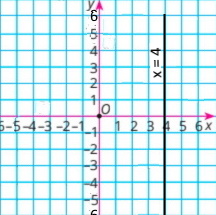
в) x = –4	г) 3у = –15

Завдання 1029

а) x + 0у = 4	б) 0 • x + 3у = 6
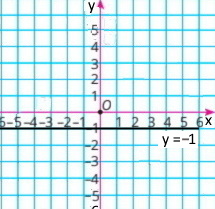
а) 2x = 6	в) у = –1

Завдання 1030

За допомогою ресурсу Desmos Calculator побудуй графік рівняння 0,2x + 3у = 1. Зверни увагу на запис десяткового дробу. В другому рядку введи своє рівняння і побудуй його графік. Друге рівняння: x + 3y = 1

  

Завдання 1031

Склади три різні рівняння, графіки яких проходять через одну й ту саму точку:

а) A(4;3) x + 2y = 10 3x – y = 9 2x – 3y = –1

б) С(0;–3) x + 3y = –9 5x – y = 3 2x + y = –3

в) K(–2; 4) x + 2y = 6 2x – y = –8 –x + y = 6

г) М(1; 0) 2x + y = 2 x – 3y = 1 3x + 2y = 3

Завдання 1033

Склади рівняння, графік якого проходить через початок координат і задану точку.

За умовою графік рівняння проходить через початок координат, тому рівняння y = kx.

а) X(2;2); Точка лежить на прямій у = kx, тому 2 = 2k, k = 1. Рівняння y = x

б) Y(–5;2). Точка лежить на прямій у = kx, тому 2 = –5k; k = –2/5 = –0,4.

Рівняння y = –0,4x

 

Завдання 1034

За умовою графік рівняння проходить через початок координат, тому рівняння y = kx.

а) Р(–4;–6); Точка лежить на прямій у = kx, тому –6 = –4k, k = 3/2 = 1,5.

Рівняння y = 1,5x

б) T(3; –1). Точка лежить на прямій у = kx, тому –1 = 3k, k = –1/3.

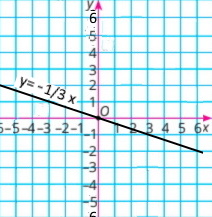
Рівняння y = –1/3x

 

Завдання 1035

Склади рівняння, графік якого перетинає осі координат у точках.

а) A(–3;0) і B(0;1)	б) M(4;0) і N(0;5)
y = kx + b Точка B(0;1) лежить на прямій. 1 = 0 • k + b b = 1 y = kx + 1 Точка A(–3;0) лежить на прямій. 0 = –3k + 1 3k = 1 k = 1/3 Рівняння: y = 1/3x + 1	y = kx + b Точка M(4;0) лежить на прямій. 5 = 0 • k + b b = 5 y = kx + 5 Точка N(0;5) лежить на прямій. 0 = 4k + 5 –4k = 5 k = –5/4 = –1,25 Рівняння: y = –1,25x + 5

Завдання 1036

а) P(0;–3) і Q(3;0)	б) C(0;–4) і D(–2;0)
y = kx + b Точка P(0;–3) лежить на прямій. –3 = 0 • k + b b = –3 y = kx – 3 Точка Q(3;0) лежить на прямій. 0 = 3k – 3 3k = 3 k = 1 Рівняння: y = x – 3	y = kx + b Точка C(0;–4) лежить на прямій. –4 = 0 • k + b b = –4 y = kx – 4 Точка D(–2;0) лежить на прямій. 0 = –2k – 4 2k = –4 k = –2 Рівняння: y = –2x – 4

Завдання 1037

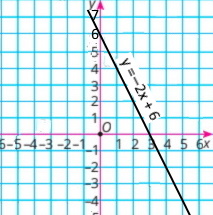
Запиши рівняння, графіки яких зображено на малюнку 23.6.

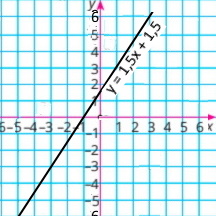
a) (0;2) і (–1;0)	б) (0;–4) і (4;0)
y = kx + b Точка (0;2) лежить на прямій. 2 = 0 • k + b b = 2 y = kx + 2 Точка (–1;0) лежить на прямій. 0 = –k + 2 k = 2 Рівняння: y = 2x + 2	y = kx + b Точка (0;–4) лежить на прямій. –4 = 0 • k + b b = –4 y = kx – 4 Точка (4;0) лежить на прямій. 0 = 4k – 4 4k = 4 k = 1 Рівняння: y = x – 4
c) (0;2) і (2;0)	d) (0;–2) і (–4;0)
y = kx + b Точка (0;2) лежить на прямій. 2 = 0 • k + b b = 2 у = kk + 2 Точка (0;2) лежить на прямій. 0 = 2k + 2 2k = –2 k = –1 Рівняння: y = –x + 2	y = kx + b Точка (0;–2) лежить на прямій. –2 = 0 • k + b b = –2 у = –kх – 2 Точка (–4;0) лежить на прямій. 0 = –4k – 2 4k = –2 k = –1/2 Рівняння: y = –1/2 x – 2

Завдання 1038

Склади рівняння, графік якого проходить паралельно графіку рівняння 2х – у = 0 через точку:

За умовою графік рівняння паралельний графіку рівняння 2х – у = 0, тому шукане рівняння має вигляд: 2х – у = с, де с ≠ 0.

а) K(4;2)	б) L(0;5)
2х – у = с 2 • 4 – 2 = с с = 6 Рівняння: 2x – y = 6	2х – у = с 2 • 0 – 5 = c c = –5 Рівняння: 2x – y = –5

Завдання 1039

Склади рівняння, графік якого проходить паралельно графіку рівняння 3х – у = 0 через точку

За умовою графік рівняння паралельний графіку рівняння 3х – у = 0, тому шукане рівняння має вигояд: 3х – у = с, де с ≠ 0.

а) M(–3;0)	б) A(2;–1)
3х – у = с 3 • (–3) – 0 = с с = –9 Рівняння: 3x – y = –9	3х – у = с 3 • 2 – (–1) = c c = 7 Рівняння: 3x – y = 7

ЦІКАВІ ЗАДАЧІ

Завдання 1040

Чи правильно, що графіком рівняння |х – 2| + |у – 3| = 0 є одна точка K(2;3)?

х – 2  = 0 і у – 3 = 0

х = 2         у = 3

Розв'язок рівняння (2;3), тому графіком дійсно є одна точка K(2;3)

А рівняння |х – 2| = |у – 3|?

x – 2 = y – 3   або x – 2 = –(y – 3) 

x – у = –3 + 2      x – 2 = –y + 3

х – у = –1             х + у = 3 + 2

                         х + у = 5

Графіком рівняння |х – 2| = |у – 3| є дві прямі: x – у = –1 і х + у = 5

 

Завдання 1041

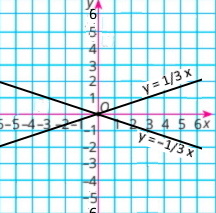
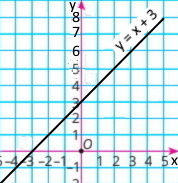
а) x² – 9у² = 0    (x – 3у)(х + 3у) = 0    x – 3у = 0  або х + 3у = 0    у = 1/3 х і у =  –1/3 х	б) (у – 2)² = (x + 1)²     у – 2 = x + 1     у = x + 3

ВПРАВИ ДЛЯ ПОВТОРЕННЯ

Завдання 1042

Оля працює вебдизайнеркою, щодня виконуючи певні проєкти для соціальних мереж замовників. Проаналізуй її заробіток продовж 5 днів.

а) найменше Оля заробила в середу (1500 грн);

б) найбільше Оля заробила в четвер (3000 грн):

Оля заробила у вівторок 2500 грн.

Чи вистачить їй заробітку за тиждень, щоб придбати онлайн–курс для підвищення кваліфікації, ціна якого 11500 грн? 

2000 + 2500 + 1500 + 3000 + 2000 = 11000 (грн) – тижневий заробіток Олі.

11000 < 11500, тому не вистачить.

 

Завдання 1043 Рівняння

а) x² = 64     x = 8 або x = –8

б) (x – 2)² = 25 x – 2 = 5 або x – 2 = –5 x = 7            x = –3

Завдання 1044

З Києва до Одеси виїхав автобус, а через 20 хв слідом за ним – легковий автомобіль, який через 1 год наздогнав автобус. З якою швидкістю їхав автобус, якщо швидкість автомобіля дорівнювала 80 км/год?

Нехай швидкість автобуса х км/год, тоді автобус проіхав 1 1/3 х км, а автомобіль проїхав 80 км. Складаємо рівняння:

1 1/3х = 80

4/3 х = 80

х = 80 : 4/3

х = 80 • 3/4

х = 60 (км/год) – швидкість автобуса.

Відповідь: 60 км/год.

Інші завдання дивись тут...