Інші завдання дивись тут...

ЗАВДАННЯ ДЛЯ САМОСТІЙНОЇ РОБОТИ

ВАРІАНТ І

Завдання 1 Розв’язування системи рівнянь

{5х + 6у = 4

  3х – 2у = 8       |•3

{5х + 6у = 4

 9х – 6у = 24

 14x = 28

х = 2

Підставляємо знайдене значення х у рівняння 3х – 2у = 8:

3 • 2 – 2y = 8

6 – 2y = 8

2y = –2

y =–1

Відповідь: (2;–1)

 

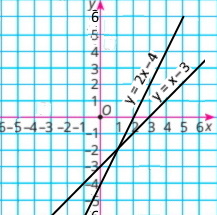
Завдання 2 Розв’язування графічно системи рівнянь

{2х – у = 4   х – у = 3		Розв'язок системи рівнянь (–1;–2)
у = 2х – 4 х 0 2 у –4 0	у = х – 3  х 0 1 у –3 –2

Завдання 3

2 кг помідорів на 16 грн дорожчі за 3 кг огірків. Скільки коштує 1 кг огірків і 1 кг помідорів, якщо за 1 кг помідорів і 4 кг огірків заплатили 107 грн?

Розв'язання

Нехай ціна помідорів — x грн, а огірків — y грн. Складаємо систему рівнянь:

{x + 4y = 107
 2х – 3у = 16

{x = 107 – 4y

 2(107 – 4y) – 3y = 16

Розв'язуємо рівняння:

2(107 – 4y) – 3y = 16

214  – 8y – 3y = 16

–11y = –198

y = 18

Підставляємо знайдене значення у в рівняння х = 107 – 4у:

x = 107 – 4 • 18

х = 107 – 72

х = 35

Відповідь: ціна помідорів 35 грн і ціна огірків 18 грн.

 

ВАРІАНТ ІI

Завдання 1

4х + 3у = –1

2х – 5у = 19     |•(–2)

{4х + 3у = –1

 –4х + 10у = –38

      13у = –39

у = –3

Підставляємо знайдене значення у в рівняння 2х – 5у = 19:

2х – 5 • (–3) = 19

2х + 15 = 19

2х = 4

х = 2

Відповідь: (2;–3)

 

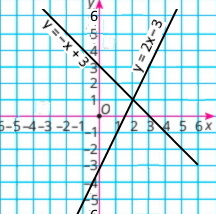
Завдання 2

{2х – у = 3  х + у = 3		Розв'язок системи рівнянь (2;1)
у = 2х – 3 х 0 2 у –3 1	у = –х + 3  х 0 –3 у 3 0

Завдання 3

3 кг моркви на 4 грн дорожчі за 2 кг картоплі. Скільки коштує 1 кг моркви і 1 кг картоплі, якщо за 5 кг картоплі і 1 кг моркви заплатили 58 грн?

Розв'язання

Нехай ціна моркви — x грн, а картоплі — y грн. Складаємо систему рівнянь:

{x + 5y = 58
 3х – 2у = 4

{x = 58 – 5y
 3(58 – 5y) – 2y = 4

Розв'язуємо рівняння:

3(58 – 5y) – 2y = 4

174  – 15y – 2y = 4

–17y = –170

y = 10

x = 58 – 5 • 10

х = 58 – 50

х = 8

Відповідь: ціна моркви 8 грн і ціна картоплі 10 грн.

 

ВАРІАНТ ІII

Завдання 1

5х – 2у = 7      |•4

3х + 8у = –5          

{20х – 8у = 28

 3х + 8у = –5

 23x = 23

х = 1

Підставляємо знайдене значення х у рівняння 5х – 2у = 7:

5 • 1 – 2y = 7

5 – 2y = 7

–2y = 2

y =–1

Відповідь: (1;–1)

 

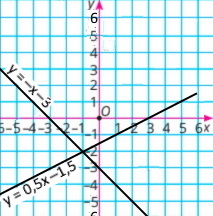
Завдання 2

{х – 2у = 3  х + у = –3		Розв'язок системи рівнянь (–1;–2)
у = 0,5х – 1,5 х –1 1 у –2 –1	у = –х – 3  х 0 –3 у –3 0

Завдання 3

4 кг печива на 40 грн дорожчі за 2 кг цукерок. Скільки коштує 1 кг печива і 1 кг цукерок, якщо за 3 кг печива і 1 кг цукерок заплатили 355 грн?

Розв'язання

Нехай ціна печива — x грн, а цукерок — y грн. Складаємо систему рівнянь:

{3x + y = 355
 4х – 2у = 40

{у = 355 – 3х
 4х – 2(355 – 3х) = 40

Розв'язуємо рівняння:

4х – 2(355 – 2х) = 40

4х  – 710 + 4х = 40

8х = 670

х = 83,75

Підставляємо знайдене значення х у рівняння у = 355 – 3х:

у = 355 – 3 • 83,75

у = 355 – 251,25

у = 103,75

Відповідь: ціна печива 83,75 грн і ціна цукерок 103,75 грн.

 

ГОТУЄМОСЯ ДО ТЕМАТИЧНОГО ОЦІНЮВАННЯ

Тестові завдання № 7

Завдання 1

На графіку рівняння 3x – 5y = 6,2 взято точку з абсцисою 0,4. Яка ордината цієї точки?

3 • 0,4 – 5y = 6,2

1,2 – 5у = 6,2

–5у = 5

у = –1, тому Б –1

 

Завлання 2

Розв’язком якого рівняння є пара чисел (2; 3)?

А 2x + y = 7, бо 2 • 2 + 3 = 4 + 3 = 7

 

Завдання 3

Яке з рівнянь не має розв’язків?

А x⁴ +  y⁴ = –5, бо сума невід'ємних чисел не може бути від'ємною.

 

Завдання 4

Графіком якого рівняння є пряма, паралельна осі ординат?

Г x = 2, бо у = 0, а х – будь–яке число

 

Завдання 5

При якому значенні a графік рівняння 2x + ay = 4 проходить через точку (1;2)?

2 • 1 + 2a = 4

2 + 2а = 4

2а = 2

а = 1, тому В 1

 

Завдання 6 Розв’язок системи рівнянь

{х + у = 14

 х – у = 8

 2х = 22

х = 11

11 + у = 14

у = 3, тому А (11;3)

 

Завдання 7

{х = у

 х + у = 10

Розв'язуємо рівняння:

у + у = 10

2у = 10

у = 5

Підставляємо знайдене значення у в рівняння х = у:

х = 5, тому Б (5;5)

 

Завдання 8

Знайди координати точки перетину графіків рівнянь 2x – 3y = 16 і x + 2y = 1.

{2x – 3y = 16

 x + 2y = 1

{2(1 – 2у) – 3y = 16

 x = 1 – 2у

Розв'язуємо рівняння:

 

 

 

 

 

 

 

 

 

Завдання 9

Скільки спільних точок мають графіки рівнянь 2x + 3y = 7 і 2x – 3y = 7? А одну

 

Завдання 10 

При яких значеннях a система рівнянь має безліч розв’язків?

{3х + ау = 15

 12х – 8у = 60    |:4

{3х + ау = 15

 3х – 2у = 15

Система має безліч розв'язків, якщо а = –2, тому А –2

 

ТИПОВІ ЗАВДАННЯ ДО КОНТРОЛЬНОЇ РОБОТИ №7

Завдання 1

Через яку з точок проходить графік рівняння 3х – 5у = –2?

3 • х – 5 • 1 = 3 – 5 = –2, тому В (1;1)

 

Завдання 2

При якому значенні у пара чисел (3;у) є розв’язком рівняння:

5х + 7у = 36

5 • 3 + 7у = 36

15 + 7у = 36

7у = 21

у = 3, тому Б 3

 

Завдання 3

У якій точці графік рівняння 2х + 3у = 6 перетинає вісь абсцис?

При у = 0, 2х = 6, х = 3, тому Б (0; 3)

 

Завдання 4

Установи відповідність між значеннями а і b, заданими умовами (1–3), та кількістю розв’язків (А–Д) системи рівнянь. 1—А, 2—Г, 3—В.

 

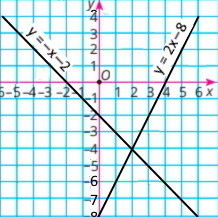
Завдання 5

{х + у = –2  2х – у = 8		Розв'язок системи рівнянь (2;–4)
у = –х – 2 х 0 1 у –2 –3	у = 2х – 8  х 0 1 у –8 –6

Завдання 6

а) {5х – 3у = –9      2х – у = –2    {5х – 3(2х + 2) = –9      у = 2x + 2 Розв'язуємо рівняння: 5х – 3(2х + 2) = –9 5х – 6х – 6 = –9 –х = –3 х = 3 Підставляємо х у рівняння у = 2х + 2: у = 2 • 3 + 2 у = 6 + 2 у = 8 Відпоівідь: (3;8)

б) (3х – 2у)/5 + (2х – у)/3 – х = 1     |•15    (4х + у)/3 – (3х + у)/2 – у = 1       |•6    3(3х – 2у) + 5(2х – у) – 15х = 15    2(4х + у) – 3(3х + у) – 6у = 6    9х – 6у + 10х – 5у – 15х = 15    8х + 2у – 9х – 3у – 6у = 6    4х – 11у = 15    –х – 7у = 6    4(–7у – 6) – 11у = 15    х = –7у – 6 Розв'язуємо рівняння: 4(–7у – 6) – 11у = 15 –28у – 24 – 11у = 15 –39у = 39 у = –1 Підставляємо у в рівняння х = –7у – 6: х = –7 • (–1) – 6 у = 7 – 6 у = 1 Відповідь: (–1;1)

Завдання 7

У сараї є гуси та кролі. У них 50 голів і 160 ніг. Скільки гусей і скільки кролів у сараї?

Розв'язання

Нехай у сараї x гусей і у кролів. У гуски 2 ноги, а в кроля 4 ноги. Складаємо систему рівнянь:

{х + у = 50

 2х + 4у = 160

{х = 50 – у

 2(50 – у) + 4у = 160

Розв'язуємо рівняння:

2(50 – у) + 4у = 160

100 – 2у + 4у = 160

2у = 60

у = 30

х = 50 – 30

х = 20

Відповідь: 20 гусей і 30 кролів.

 

Завдання 8

Знайди значення коефіцієнтів a і b рівняння ax + by = 13, якщо його графік проходить через точки M(5;–3) і N(9;5).

{5a – 3b = 13     |•5

 9a + 5b = 13     |•3

{25a – 15b = 65

 27a + 15b = 39 

 52a = 104

a = 2

Підставляємо знайдене значення a в рівняння: 5а – 3b = 13:

5 • 2 – 3b = 13

10 – 3b = 13

–3b = 3

b = –1

Відповідь: a = 2 і b = –1.

 

Додаткове завдання

Завдання 9

На складі було 1500 м³  березових і соснових дров. За перший місяць використали 15% соснових і 20% березових дров, а разом — 270 м³. Скільки соснових і скільки березових дров окремо було на складі?

Розв'язання

Нехай на складі березових х дров і соснових у дров. Складаємо систему рівнянь:

{х + у = 1500

 0,2х + 0,15у = 270

{х = 1500 – у

 0,2(1500 – у) + 0,15у = 270

Розв'язуємо рівняння:

0,2(1500 – у) + 0,15у = 270

300 – 0,2у + 0,15у = 270

–0,05у = 30

у = 600

х = 1500 – 600

х = 900

Відповідь: 600 м³ березових дров і 900 м³ соснових дров.

Інші завдання дивись тут...