Завдання 1141 Знайди два числа, якщо:
|
а) їх сума дорівнює 40, а відношення — 3; |
б) їх сума дорівнює 40, а різниця — 20; |
в) їх різниця дорівнює 10, а відношення — 3. |
|
{x + y = 40 y = 3x {x + 3х = 40 y = 3x Розв'язуємо рівняння: x + 3х = 40 4х = 40 х = 10 у = 3 • 10 у = 30 Відповідь: 10 і 30. |
{x + y = 40 y – x = 20 {x + y = 40 –x + у = 20 2y = 60 y = 30 30 – x = 20 x = 10 Відповідь: 10 і 20. |
в) {y – x = 10 y = 3x {3х – x = 10 y = 3x Розв'язуємо рівняння: 3x – x = 10 2x = 10 x = 5 у = 3 • 5 у = 15 Відповідь: 5 і 15 |
Завдання 1142
|
Схема ліворуч |
Схема праворуч |
|
{x + y = 37 y – x = 7 |
{х + у = 80 y = 3x |
Завдання 1143, 1144
|
Знайди два числа, сума яких дорівнює 35,5, а різниця — 12,5. Розв'язання Нехай перше число x, а друге – y. Складаємо систему рівнянь: 2x = 48 Підставляємо х в рівняння х + у = 35,5: 24 + y = 35,5 Відповідь: 24 і 11,5. |
Знайди два числа, півсума яких дорівнює 37,9, а піврізниця — 7,5. Розв'язання Нехай перше число x, а друге – y. Складаємо систему рівнянь: {x + y = 75,8 2x = 90,8 Підставляємо х в рівняння х + у = 75,8: 45,4 + y = 75,8 Відповідь: 45,4 і 30,4. |
Завдання 1145, 1146
|
Купили 9 м тканини двох сортів ціною по 1200 грн і 900 грн за 1 м. За всю покупку заплатили 9900 грн. Скільки метрів тканини кожного сорту купили? Розв'язання Першого сорту х метрів, а другого – у м. Складаємо систему рівнянь: {x + y = 9 {у = 9 – х 1200х + 900(9 – х) = 9900 Розв'язуємо рівняння: 1200х + 900(9 – х) = 9900 1200х + 8100 – 900х = 9900 300х = 1800 х = 6 Підставляємо х в рівняння у = 9 - х: у = 9 – 6 = 3 Відповідь: 6 м і 3 м. |
На будівництві працювали 50 мулярів і теслярів. Згодом кількість мулярів збільшилась у 2 рази, а теслярів — у 3 рази, і всіх стало 130. Скільки мулярів і теслярів було спочатку? Розв'язання Працювало х мулярів і у теслярів. Складаємо систему рівнянь: {x + y = 50 {х = 50 – у 2(50 – у) + 3y = 130 Розв'язуємо рівняння: 2(50 – у) + 3y = 130 100 – 2у + 3у = 130 у = 30 Підставляємо у в рівняння х = 50 - 30: х = 50 – 30 = 20 Відповідь: 20 мулярів і 30 теслярів. |
Завдання 1147, 1148
|
Швидкість моторного човна за течією — 23 км/год, а проти течії — 17 км/год. Знайдіть власну швидкість човна і швидкість течії. Розв'язання Нехай швидкість човна x км/год, а швидкість течії y км/год. Складаємо систему рівнянь: {x + y = 23 х – у = 17 2x = 40 x = 20 Підставляємо х в рівняння х - у = 17: 20 – y = 17 y = 3 Відповідь: 20 км/год і 3 км/год. |
Швидкість катера за течією річки — 37 км/год, а проти течії — 33 км/год. Знайди власну швидкість катера і швидкість течії. Розв'язання Нехай швидкість катера x км/год, а швидкість течії y км/год. Складаємо систему рівнянь: 2x = 70 x = 35 Підставляємо х в рівняння х + у = 37: 35 + y = 37 y = 2 Відповідь: 35 км/год і 2 км/год. |
Завдання 1149, 1150
|
Дві велосипедистки виїхали одночасно з двох сіл, відстань між якими становить 9 км, і зустрілися через 0,5 год. Визнач швидкість руху кожної, якщо швидкість першої велосипедистки на 1,6 км/год більша за швидкість другої велосипедистки. Розв'язання Нехай швидкість першої х км/год, а другої – у км/год. Складаємо систему рівнянь: {х – у = 1,6 0,5х + 0,5у = 9 {х = 1,6 + у 0,5(1,6 + у) + 0,5у = 9 Розв'язуємо рівняння: 0,5(1,6 + у) + 0,5у = 9 0,8 + 0,5у + 0,5у = 9 у = 8,2 Підставляємо у в рівняння х = 1,6 + у: х = 1,6 + 8,2 = 9,8 Відповідь: 8,2 км/год і 9,8 км/год. |
Два туристи вийшли одночасно з двох міст, відстань між якими — 57 км, і зустрілися через 6 год (мал. 27.3). З якою швидкістю йшов кожний, якщо перший до зустрічі пройшов на 3 км більше, ніж другий? Розв'язання Нехай швидкість першого x км/год, а другого — y км/год. Складаємо систему рівнянь: 12х = 60 х = 5 Підставляємо х в рівняння 6х - 6у = 3: 30 – 6у = 3 6у = 27 у = 4,5 Відповідь: 5 км/год і 4,5 км/год. |
Завдання 1151
Туристи проїхали 570 км. 6 год вони їхали поїздом і 3 год — автобусом. Знайди швидкість поїзда, якщо вона на 5 км/год більша за швидкість автобуса. Доповни таблицю та розв’яжи задачу.
| v, км/год | t, год | s, км | |
|
Поїзд |
х |
6 | 6х |
|
Автобус |
у |
3 | 3у |
Розв'язання
{6х + 3у = 570
х – у = 5
{6(у + 5) + 3у = 570
х = у + 5
Розв'язуємо рівняння:
6(у + 5) + 3у = 570
6у + 30 + 3у = 570
9у = 540
у = 60
Підставляємо у в рівняння х = у + 5:
х = 60 + 5 = 65
Відповідь: швидкість поїзда 65 км/год і швидкість автобуса 60 км/год.
Завдання 1152
Три «дорослі» тополі й 5 «дорослих» лип з травня по вересень поглинають 212 кг вуглекислого газу. Такі самі 5 тополь і 3 липи поглинають 268 кг вуглекислого газу. Скільки вуглекислого газу поглинає за цей час кожне дерево?
Розв'язання
Нехай вуглекислого газу одна тополя поглинає x кг, а одна липа — y кг. Складаємо систему рівнянь:
{3x + 5y = 212 |•5
5x + 3y = 268 |•(–3)
{15x + 25y = 1060
–15x – 9y = –804
16y = 256
y = 16
Підставляємо у в рівняння 3х + 5у = 212:
3x + 80 = 212
3x = 132
x = 44
Відповідь: тополя поглинає вуглекислого газу 44 кг і липа – 16 кг.
Завдання 1153
На годівлю 10 коней і 16 корів щодня відпускали 160 кг сіна, причому 5 коней одержували на 5 кг сіна більше, ніж 7 корів. Скільки кілограмів сіна давали щодня коневі й скільки корові?
Розв'язання
Нехай щоденна кількість сіна для коня дорівнює x кг, а для корови — y кг. Складаємо систему рівнянь:
{10x + 16y = 160
5x – 7y = 5 |•(–2)
{10x + 16y = 160
–10x + 14y = –10
30y = 150
y = 5
Підставляємо у в рівняння 5х - 7у = 5:
5x – 35 = 5
5x = 40
x = 8
Відповідь: 8 кг і 5 кг.
Завдання 1154
Периметр ділянки прямокутної форми дорівнює 168 м. Знайди довжини її сторін, якщо одна з них на 8 м довша.
Розв'язання
Нехай довжина більшої сторони прямокутної ділянки x м, а меншої — у м. Складаємо систему рівнянь:
{х – у = 8
2х + 2у = 168
{х = у + 8
2(у + 8) + 2у = 168
Розв'язуємо рівняння:
2(у + 8) + 2у = 168
2у + 16 + 2у = 168
4у + 16 = 168
4у = 152
у = 38
Підставляємо у в рівняння х = у + 8:
х = 38 + 8 = 46
Відповідь: 38 м і 46 м.
Завдання 1155
Мати старша за доньку на 24 роки, а донька молодша від матері втричі. Скільки років матері й скільки доньці?
Розв'язання
Нехай матері виповнилося x років, а доньці – у років. Складаємо систему рівнянь:
{x – у = 24
х = 3у
{3у – у = 24
х = 3у
Розв'язуємо рівняння:
3у – у = 24
2у = 24
у = 12
Підставляємо у в рівняння х = 3у:
х = 3 • 12 = 36
Відповідь: 36 років і 12 років.
Завдання 1156
Знайди довжини сторін рівнобедреного трикутника, якщо його периметр дорівнює 82 см, а основа більша за бічну сторону на 10 см.
Розв'язання
Нехай бічна сторона рівнобедреного трикутника дорівнює x см, а основа – у см. Складаємо систему рівнянь:
{у – х = 10
2х + у = 82
{у = х + 10
2х + (х + 10) = 82
Розв'язуємо рівняння:
2х + х + 10 = 82
3х = 72
х = 24
Підставляємо х в рівняння у = х + 10:
у = 24 + 10 = 34
Відповідь: 24 см, 24 см, 34 см.
Завдання 1157
Скільки років Антону й Насті, якщо разом їм — сімнадцять, і тепер їй вдвічі більше, ніж було Антону вісім років тому?
Розв'язання
Нехай Антону x років, а Насті у років. Складаємо систему рівняннь:
{х + у = 17
у = 2(х – 8)
{х + (2х – 16) = 17
у = 2х – 16
Розв'язуємо рівняння:
х + 2х – 16 = 17
3х = 33
х = 11
Підставляємо х в рівняння у = 2х - 16:
у = 22 – 16 = 6
Відповідь: 11 років і 6 років.
Завдання 1158
У двох рядах паркувального майданчика 65 автомобілів. У І ряді на 7 автомобілів більше, ніж у ІІ. Скільки автомобілів у кожному ряді?
Розв'язання
Нехай у I ряді x автомобілів, а в II – у автомобілів. Складаємо рівняння:
{х – у = 7
х + у = 65
2х = 72
х = 36
Підставляємо х в рівняння х + у = 65:
36 + у = 65
у = 29
Відповідь: 36 автомобілів і 29 автомобілів.
Завдання 1159
На двох полицях разом 78 книжок. Якщо з другої полиці переставити на першу 9 книжок, то на обох полицях книжок стане порівну. Скільки книжок на кожній полиці?
Розв'язання
Нехай на першій полиці x книжок, а на другій – у книжок. Складаємо систему рівняннь:
{х + у = 78
х + 9 = у – 9
{х + у = 78
х – у = –18
2х = 60
х = 30
Підставляємо х в рівняння х + у = 78:
30 + у = 78
у = 48
Відповідь: 30 книжок і 48 книжок.
Завдання 1160
There are 72 students in two seventh grades. If 2 students moved from class 7A to class 7B, there would be an equal number of students in both classes. How many students are in each class?
Розв'язання
Нехай в 7А класі навчаються x учнів, а в 7В класі – у учнів. Складаємо систему рівнянь:
{х + у = 72
х – 2 = у + 2
{х + у = 72
х – у = 4
2х = 76
х = 38
Підставляємо х в рівняння х + у = 72:
38 + у = 72
у = 34
Answer: в 7А класі навчаються 38 учнів і в 7В – 34 учні.
Завдання 1161
|
а) Різниця двох чисел дорівнює 4, а різниця їх квадратів — 44. Знайди ці числа. Розв'язання Нехай перше число дорівнює х, а друге – y. Складаємо систему рівнянь: {х – y = 4 х² – у² = 44 {х = y + 4 (у + 4)² – у² = 44 Розв'язуємо рівняння: (у + 4)² – у² = 44 у² + 8у + 16 – у² = 44 8у = 28 у = 3,5 Підставляємо у в рівняння х = у + 4: х = 3,5 + 4 = 7,5 Відповідь: 7,5 і 3,5. |
б) Знайди два числа, якщо відомо, що їх сума дорівнює 12, а різниця квадратів — 60. Розв'язання Нехай перше число дорівнює х, а друге – y. Складаємо систему рівнянь: {х + y = 12 х² – у² = 60 {х = 12 – у (12 – у)² – у² = 60 Розв'язуємо рівняння: (12 – у)² – у² = 60 144 – 24у + у² – у² = 60 –24у = –84 у = 3,5 Підставляємо у в рівняння х = 12 - у: х = 12 – 3,5 = 8,5 Відповідь: 8,5 і 3,5. |
Завдання 1162
|
Довжина болта і двох гайок дорівнює 250 мм. Знайдіть довжину болта і довжину гайки, якщо болт на 130 мм довший за гайку. Розв'язання Нехай довжина болта дорівнює x мм, а гайки – y мм. Складаємо систему рівнянь: {x + 2у = 250 x – у = 130 {130 + у + 2у = 250 x = 130 + у Розв'язуємо рівняння: 130 + у + 2у = 250 130 + 3у = 250 3у = 120 у = 40 Підставляємо у в рівняння х = 130 + у: х = 130 + 40 = 170 Відповідь: 170 мм і 40 мм. |
Маса грушки більша від маси яблука на 50 г. Знайдіть масу яблука і масу грушки, якщо маса трьох таких яблук дорівнює масі двох таких грушок. Розв'язання Нехай маса яблука x г, а маса грушки y г. Складаємо систему рівнянь: {х – у = 50 3x = 2y {1,5x – x = 50 y = 1,5x Розв'язуємо рівняння: 1,5x – x = 50 0,5x = 50 х = 100 Підставляємо х в рівняння у = 1,5х: у = 150 Відповідь: 100 г і 150 г. |
Завдання 1163
Стародавня китайська задача. Скільки в клітці фазанів і кролів, якщо разом у них 35 голів і 94 ноги?
Розв'язання
Нехай у клітці x фазанів і у кролів. Складаємо систему рівнянь:
{х + у = 35
2х + 4у = 94
{х = 35 – у
2(35 – у) + 4у = 94
Розв'язуємо рівняння:
2(35 – у) + 4у = 94
70 – 2у + 4у = 94
2у = 24
у = 12
Підставляємо у в рівняння х = 35 - у:
х = 35 – 12 = 23
Відповідь: 23 фазани і 12 кролів.
Завдання 1164
Стародавня китайська задача. 5 волів і 2 барани коштують 11 таєлів, а 2 воли і 8 баранів — 8 таєлів. Скільки баранів можна купити за гроші, одержані від продажу 5 волів?
Розв'язання
Нехай ціна вола x таєлів, а барана y таєлів. Складаємо систему рівнянь:
{5x + 2y = 11 |•(–2)
2x + 8y = 8 |:2
{–10x – 4y = –22
x + 4y = 4
–9х = –18
х = 2
Підставляємо х в рівняння х + 4у = 4:
2 + 4у = 4
4у = 2
у = 0,5
5 • 2 = 10 (т.) – коштують 5 волів;
10 : 0,5 = 20 (б.) – можна отримати баранів за ці кошти.
Відповідь: 20 баранів.
Завдання 1165
Стародавня грецька задача. Навантажені осел і мул ідуть повільно. Осел скаржиться на важку ношу, мул йому відповідає: «Чого ти скаржишся? Коли я взяв би один твій мішок, то моя ноша стала б удвічі важчою від твоєї. А коли ти взяв би один мій мішок, то твоя ноша дорівнювала б моїй». По скільки мішків несли осел і мул?
Розв'язання
Нехай осел несе x мішків, а мул — y мішків. Складаємо систему рівнянь:
{y + 1 = 2(x – 1)
x + 1 = y – 1
{y + 1 = 2((у – 2) –1)
x = y – 2
Розв'язуємо рівняння:
y + 1 = 2((у – 2) –1)
y + 1 = 2(у – 3)
y + 1 = 2у – 6
2у – у = 1 + 6
у = 7
Підставляємо у в рівняння х = у - 2:
х = 7 – 2 = 5
Відповідь: 5 мішків і 7 мішків.
Завдання 1166
Півсума двох чисел більша від меншого з них на 5, а від пів різниці — на 1. Знайди ці числа.
Розв'язання
Нехай більше число дорвнює x, а менше – y. Складаємо систему рівнянь:
{(x + y)/2 – y = 5 |•2
(х + у)/2 – (x – y)/2 =1 |•2
{x + y – 2у = 10
x + y – (х – у) = 2
{x – y = 10
2у = 2
{x – 1 = 10
у = 1
{x = 11
у = 1
Відповідь: 11 і 1.
Завдання 1167
Піврізниця двох чисел менша від більшого з них на 13, а від їх різниці — на 12. Знайди ці числа.
Розв'язання
Нехай більше число дорівнює x, а менше – y. Складаємо систему рівнянь:
{х – (x – y)/2 = 13 |•2
(x – у) – (х – y)/2 = 12 |•2
{2х – (x – y) = 26
2(x – у) – (х – у) = 24
{2х – x + y = 26
2x – 2у – х + у = 24
{х + у = 26
х – у = 24
2х = 50
х = 25
Підставляємо х в рівняння х + у = 26:
25 + у = 26
у = 1
Відповідь: 25 і 1.
Завдання 1168
Різниця квадратів двох додатних чисел і квадрат їх різниці дорівнюють відповідно 275 і 121. Знайди ці числа.
Розв'язання
Нехай невідомі числа – x і y. Складаємо систему рівнянь:
{x² – y² = 275
(x – y)² = 121
{(x – y)(х + у) = 275
(x – y)² = 11²
Розв'язуємо дві системи рівнянь:
|
{(x – y)(x + y) = 275 x – y = 11 {11(x + y) = 275 x – y = 11 {x + y = 25 x – y = 11 2x = 36 x = 18 Підставляємо х в рівняння х - у = 11 18 – y = 11 y = –7 |
{(x – y)(x + y) = 275 x – y = –11 {–11(x + y) = 275 x – y = –11 {x + y = –25 x – y = –11 2x = –36 x = –18 Підставляємо х в рівняння х - у = -11: –18 – y = –11 y = 7 |
|
Відповідь: 18 і –7 або –18 і 7 |
|
Завдання 1169
Відстань 320 км моторний човен проходить за течією річки за 8 год, а проти течії — за 10 год. Знайди швидкість течії річки і власну швидкість моторного човна.
Розв'язання
Нехай власна швидкість човна х км/год, а швидкість течії річки у ки/год.
| v, км/год | t, год | s, км | |
|
За течією |
х + у |
8 | 8(х + у) |
|
Проти течії |
х – у |
10 | 10(х – у) |
Складаємо систему рівнянь:
{8(х + у) = 320
10(х – у) = 320 |:10
{8х + 8у = 320
х – у = 32 |•8
{8х + 8у = 320
8х – 8у = 256
16х = 576
х = 36
Підставляємо х в рівняння х - у = 32:
36 – у = 32
у = 4
Відповідь: 4 км/год і 36 км/год.
Завдання 1170
Відстань 210 км катер проходить за течією річки за 5 год, а проти течії — за 6 год. Знайди швидкість течії річки і власну швидкість катера.
Розв'язання
Нехай власна швидкість катера х км/год, а швидкість течії річки у y км/год.
| v, км/год | t, год | s, км | |
|
За течією |
х + у |
5 | 5(х + у) |
|
Проти течії |
х – у |
6 | 6(х – у) |
Складаємо систему рівнянь:
{5(х + у) = 210 |:10
6(х – у) = 210
{х + у = 42 |•6
6х – 6у = 210
{6х + 6у = 252
6х – 6у = 210
12х = 462
х = 38,5
Підставляємо х в рівняння х + у = 42:
38,5 + у = 42
у = 3,5
Відповідь: 3,5 км/год і 38,5 км/год.
Завдання 1171
Якщо з одного пункту одночасно і в одному напрямку виїдуть велосипедист і мотоцикліст, то через 2 год відстань між ними буде дорівнювати 14 км. Якщо ж вони виїдуть одночасно в протилежних напрямках, то через 3 год відстань між ними становитиме 174 км (мал. 27.6). Знайди швидкість кожного з них.
Розв'язання
Нехай швидкість мотоцикліста х кмгод, а велосипедиста – y км/год. Складаємо систему рівнянь:
{2(х – у) = 14
3(х + у) = 174
{х – у = 7
x + у = 58
2х = 65
х = 32,5
Підставляємо х в рівняння х - у = 7:
32,5 – у = 7
у = 25,5
Відповідь: швидкість мотоцикліста 32,5 км/год і швидкість велосипедиста 25,5 км/год.
Завдання 1172
Якби велосипедистка збільшила швидкість на 3 км/год, то відстань між пунктами A і B проїхала б на 1 год швидше. А якби їхала зі швидкістю на 2 км/год меншою, то їхала б на 1 год довше. Знайдіть швидкість велосипедистки і відстань між пунктами A і B.
Розв'язання
Нехай швидкість велосипедистки х кмгод, а час руху – y год. Складаємо систему рівнянь:
{ху = (х + 3)(у – 1)
ху = (х – 2)(у + 1)
{ху = ху – х + 3у – 3
ху = ху + х – 2у – 2
{ху – ху + х – 3у = –3
ху – ху – х + 2у = –2
{х – 3у = –3
–х + 2у = –2
–у = –5
у = 5
Підставляємо у в рівняння х - 3у = -3:
х – 15 = –3
х = 12
12 • 5 = 60
Відповідь: 12 км/год і 60 км.
Завдання 1173
Якби мотоциклістка збільшила швидкість на 24 км/год, то відстань між містами A і B проїхала б на 1 год швидше. А якби зменшила швидкість на 12 км/год, то їхала б на 1 год довше. Знайди швидкість мотоциклістки і відстань між містами A і B.
Розв'язання
Нехай швидкість мотоциклістки х кмгод, а час руху – y год. Складаємо систему рівнянь:
{ху = (х + 24)(у – 1)
ху = (х – 12)(у + 1)
{ху = ху – х + 24у – 24
ху = ху + х – 12у – 12
{ху – ху + х – 24у = –24
ху – ху – х + 12у = –12
{х – 24у = –24
–х + 12у = –12
–12у = –36
у = 3
Підставляємо у в рівняння х - 24у = -24:
х – 72 = –24
х = 48
48 • 3 = 144
Відповідь: 48 км/год і 144 км.
Завдання 1174
На двох рахунках разом 10000 гривень. Якщо з першого перевести половину грошей на другий, то на другому стане у чотири рази більше грошей, ніж залишиться на першому рахунку. Скільки грошей на рахунках?
Розв'язання
Нехай на першому рахунку х грн, а на другому – y грн. Складаємо систему рівнянь:
{х + у = 10000
у + 0,5х = 4(х – 0,5х)
{у = 10000 – х
10000 – х + 0,5х = 4(х – 0,5х)
Розв'язуємо рівняння:
10000 – х + 0,5х = 4х – 0,5х
–х + 0,5х – 4х + 0,5х = –10000
–4х = –10000
х = 2500
Підставляємо х в рівняння у = 10000 - х:
у = 10000 – 2500 = 7500
Відповідь: 2500 грн і 7500 грн.
Завдання 1175
На двох полицях разом 80 книжок. Якщо з другої полиці третину книжок переставити на першу, то на першій стане у три рази більше книжок, ніж залишиться на другій. Скільки книжок на кожній полиці?
Розв'язання
Нехай на першій полиці х книжок, а на другій – y книжок. Складаємо систему рівнянь:
{х + у = 80
х + 1/3 у = 3 • 2/3 у |•3
{х + у = 80
3х + у = 6у
{х = 80 – у
3(80 – у) = 5у
Розв'язуємо рівняння:
3(80 – у) = 5у
240 – 3у = 5у
–3у – 5у = –240
–8у = –240
у = 30
Підставляємо у в рівняння х = 80 - у:
х = 80 – 30 = 50
Відповідь: 50 книжок і 30 книжок.
Завдання 1176
В одному ящику великі і малі свічки. Всього їх 100. За перший день використали 35 % малих свічок і 40 % великих свічок. Скільки свічок кожного виду в ящику, якщо всього використали 38 свічок?
Розв'язання
Нехай малих було х свічок, а великих – y свічок. Складаємо систему рівнянь:
{х + у = 100
0,35х + 0,4у = 38
{х = 100 – у
0,35(100 – у) + 0,4у = 38
Розв'язуємо рівняння:
0,35(100 – у) + 0,4у = 38
35 – 0,35у + 0,4у = 38
–0,35у + 0,4у = 38 – 35
–0,05у = 3
у = 60
Підставляємо у в рівняння х = 100 - у:
х = 100 – 60 = 40
Відповідь: 40 малих свічок і 60 великих свічок.
Завдання 1177
До магазину завезли 760 кг апельсинів і бананів. За перший день продали 30 % апельсинів і 40 % бананів. Скільки завезли апельсинів і скільки бананів, якщо апельсинів продали на 59 кг менше, ніж бананів?
Розв'язання
Нехай апельсинів завезли х кг, а бананів – y кг. Складаємо систему рівнянь:
{х + у = 760
0,4у – 0,3х = 59
{у = 760 – х
0,4(760 – х) – 0,3х = 59
Розв'язуємо рівняння:
0,4(760 – х) – 0,3х = 59
304 – 0,4х – 0,3х = 59
–0,4х – 0,3х = 59 – 304
–0,7х = –245
х = 350
Підставляємо х в рівняння у = 760 - х:
у = 760 – 350 = 410
Відповідь: 350 кг іі 410 кг.
Завдання 1178
Якщо розсадити дітей по двоє за стіл, то не вистачить трьох столів. Якщо розсадити їх по троє, то один стіл виявиться зайвим. Скільки дітей і скільки столів?
Розв'язування
Нехай було x дітей і y столів. Складаємо систему рівнянь:
{x/2 = y + 3 |•2
x/3 = y – 1 |•3
{x = 2y + 6
x = 3y – 3
{x = 2y + 6
2у + 6 = 3y – 3
Розв'язуємо рівняння:
2у + 6 = 3у – 3
у = 9
Підставляємо у в рівняння х = 2у + 6:
х = 18 + 6 = 24
Відповідь: 24 дитини і 9 столів.
Завдання 1179
Метушливі горобці хочуть сісти на стовпці. По одному якщо сісти, двом не вистачило б місця, а як вмостяться по парі, буде вільна стовпців пара. Скільки ж там було стовпців і літало горобців?
Розв'язування
Нехай було x горобців і у стовпців. Складаємо систему рівнянь:
{х – 2 = у
x/2 = y – 2 |•2
{(2у – 4) – 2 = у
x = 2y – 4
Розв'язуємо рівняння:
(2у – 4) – 2 = у
2у – у = 4 + 2
у = 6
Підставляємо у в рівняння х = 2у - 4:
х = 12 – 4 = 8
Відповідь: 8 горобців і 6 стовпців.
Завдання 1180
По колу, довжина якого 120 м, рухаються два тіла. Вони зустрічаються кожні 10 с, рухаючись в одному напрямку, і кожні 4 с, рухаючись у протилежних напрямках. З якою швидкістю рухаються ці тіла?
Розв'язування
Нехай перше тіло рухається зі швидкістю х м/с, а друге – у м/с. Складаємо систему рівнянь:
{10х – 10у = 120 |:10
4х + 4у = 120 |:4
{x – у = 12
x + y = 30
2х = 42
х = 21
Підставляємо х в рівняння х - у = 12:
21 – у = 12
у = 9
Відповідь: 21 м/с і 9 м/с.
Завдання 1181
По колу, довжина якого 90 м, рухаються дві подружки на скейтах в одному напрямку й зустрічаються через 6 с. Знайди їх швидкість, якщо швидкість однієї в 4 рази більша за швидкість іншої.
Розв'язування
Нехай перша подружка рухається зі швидкістю х м/с, а друга – у м/с. Складаємо систему рівнянь:
{6х – 6у = 90
х = 4у
{24у – 6у = 90
х = 4у
Розв'язуємо рівняння:
24у – 6у = 90
18у = 90
у = 5
Підставляємо у в рівняння х = 4у:
х = 4 • 5 = 20
Відповідь: 20 м/с і 5 м/с.
Завдання 1182
Система з 2 сонячних батарей має загальну потужність 35 кВт. Знайди потужність кожної з них, якщо потужність однієї на 50 % більша за потужність іншої.
Розв'язування
Нехай потужність одної сонячної батареї х кВт, а другої – у кВт. Складаємо систему рівнянь:
{х + у = 35
х = 1,5у
{1,5у + у = 35
х = 1,5у
Розв'язуємо рівняння:
1,5у + у = 35
2,5у = 35
у = 14
Підставляємо у в рівняння х = 1,5у:
х = 1,5 • 14 = 21
Відповідь: 21 кВт і 14 кВт.
Завдання 1183
Мотузку завдовжки 35 м розрізали на дві частини так, що одна з них на 33 1/3% коротша від другої. Знайди довжини цих частин.
Розв'язування
Нехай більша частина має довжину х м, а менша – у м. Складаємо систему рівнянь:
{х + у = 35
х – у = 33 1/3
{х = 35 – у
35 – у – у = 33 1/3
Розв'язуємо рівняння:
35 – у – у = 33 1/3
–2у = 33 1/3 – 35
–2у = –1 2/3
–2у = –5/3
у = 5/6
Підставляємо у в рівняння х = 35 - у:
х = 35 – 5/6 = 34 1/6
Відповідь: 34 1/6 м і 5/6 м.
Завдання 1184
Найбільшими забруднювачами вод України є електроенергетика, комунальне господарство і сільське господарство — 79% від усього обсягу зливу в річки. Відомо, що відсоток зливів електроенергетики перевищує сукупні зливи сільського і комунального господарства на 7%, а зливи одного сільського господарства — на 26,5%. Який відсоток обсягу всіх зливів припадає на: а) комунальне господарство; б) електроенергетику?
ЦІКАВІ ЗАДАЧІ
Завдання 1185
Задача В. А. Лебега. Розв’яжи у цілих додатних числах систему.
{2x + 3у + 7z = 131 |•(–1)
2x + 3у + 8z = 140
{–2x – 3y – 7z = –131
2x + 3y + 8z = 140
z = 9
Підставляємо z в систему рівнянь:
{2x + 3y + 63 = 131
2x + 3y + 72 = 140
{2x + 3y = 68
2x + 3y = 68
Розв'язуємо рівняння:
2x + 3y = 68
2x = 68 – 3y
x = (68 – 3y)/2
Якщо y = 2, x = (68 – 6)/2 = 62/2 = 31, z = 9
Якщо y = 4, x = (68 – 12)/2 = 56/2 = 28, z = 9
Якщо y = 6, x = (68 – 18)/2 = 50/2 = 25, z = 9
Якщо y = 8, x = (68 – 24)/2 = 44/2 = 22, z = 9
Відповідь: (2;31;9), (4;28;9), (6;25;9), (8;22;9).
Завдання 1186
Знайди число, яке при діленні на 4, 7 і 11 дає відповідно остачі 2, 1 і 6, причому сума часток на 2 менша від половини шуканого числа.
Розв'язання
Нехай шукане число дорівнює х, а частки – l, m, n. Складаємо систему рівнянь:
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 1187
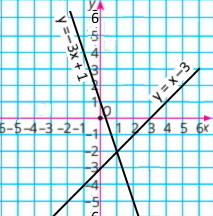
Побудуй в одній координатній площині графіки рівнянь.
|
{х – у = 3 3х + у = 1 |
Координати точки перетину (1;–2) |
||||||||||||
|
у = х – 3
|
у = –3х + 1
|
||||||||||||
Завдання 1188
Не виконуючи побудови, знайди координати точки перетину графіків рівнянь.
{x + 2у = 0
x – у = –6
{x = –2у
–2у – у = –6
Розв'язуємо рівняння:
–2y – y = –6
–3y = –6
y = 2
х = –4
Графіки перетинаються в точці з координатами (–4;2).
Завдання 1189
У фітнес–студії є ваза з резинками, які можуть брати відвідувачі.
а) найбільша кількість резинок у вазі була о 10 год
б) найменша кількість резинок у вазі була о 12 год.
Найбільша зміна кількості резинок була з 11 год до 12 год
Що відбувалось з 13:00 до 14:00: обідня перерва.