Вправа 1
6 • (а + 0,5) – 4 • (а – 2,8) = 6а + 3 – 4а + 11,2 = 2а + 14,2, тому Б. 2а + 14,2
Вправа 2 Рівняння
2,5х + 12 = 2х – 13
2,5х – 2х = –13 – 12
0,5х = –25
х = –50, тому Г. –50
Вправа 3
Сума двох чисел дорівнює 30. Одне із чисел у 1,5 рази більше за інше. Знайдіть ці числа.
х + 1,5х = 30
2,5х = 30
х = 12 – І число;
12 • 1,5 = 18 – ІІ число.
Відповідь: Б. 18 і 12.
Вправа 4
2 • (у – 3,5) = 7 + 3,6 • (2у – 1)
2у – 7 = 7 + 7,2у – 3,6
2у – 7,2у = 7 + 7 – 3,6
–5,2у = 10,4
у = 10,4 : (–5,2)
у = –2
Відповідь: Б. –2.
Вправа 5
На двох полицях стоїть 18 книжок. Якщо з першої полиці переставити на другу 2 книжки, то на першій полиці їх стане у 2 рази більше, ніж на другій. Скільки книжок стоїть на кожній полиці?
Розв'язання
Нехай на першій полиці було х книжок. Тоді на другій полиці було (18 – х) книжок. Складаємо рівняння:
х – 2 = 2(18 – х + 2)
х – 2 = 40 – 2х
Зх = 42
х = 42 : 3
х= 14
Отже, на першій полиці було 14 книжок, а на другій — 18 – 14 = 4 (книжки).
Відповідь: Б. 14 і 4.
ВАРІАНТ №2
Вправа 1
На малюнку 114 перпендикулярною до прямої AB є пряма СВ, тому В. СВ
Вправа 2
∠AOC є розгорнутим, отже, дорівнює 180°, тому Г. 180°
Вправа 3
Протилежні сторони квадрата паралельні, отже, лежать на паралельних прямих, тому
В. Протилежні сторони квадрата.
Вправа 4
Три вершини квадрата ABCD мають координати: А (–2; 4), В(5; 4) і С(5; –3). Зайдіть координати вершини D.
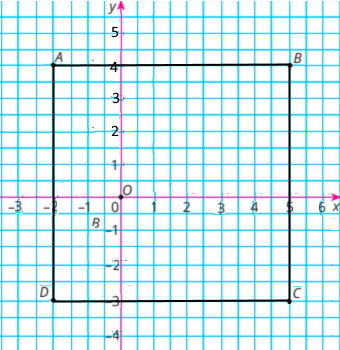
Відповідь: Г. (–2; –3)
Вправа 5
Відрізок AB точкою C поділено у відношенні 5 : 1, починаючи від точки А. Знайдіть координати точки С, якщо А(1; –6) і В (–5; –6).
5х + х = 1 + |–5|
6х = 6
х = 6 : 6
х = 1 (од.) – довжина відрізка СВ;
5x = 5 • 1 = 5 од. – довжина відрізка АС.
1 – 5 = –4 – абсциса точки С.
–6 – ордината С.
Відповідь: А. (–4; –6).
