Завдання 785 Розклад на множники
1) 7a² – 7b² = 7 (a² – b²) = 7(a – b)(a + b)
2) 3y3 – 27y = 3y (y² – 9) = 3y(y – 3)(y + 3)
3) m5 – m3 = m3(m² – 1) = m3(m – 1)(m + 1)
4) 49/64 x2y3z6 – 0,04yz8 = yz6(49/64 x²y² – 0,04z²) = yz6(7/8 xy – 0,2z)(7/8 xy + 0,2z)
Завдання 786
1) 2a² – 2b² = 2(a² – b²) = 2(a – b)(a + b)
2) cx² – cy² = c(x² – y²) = c(x – y)(x + y)
3) 3x² – 3 = 3(x² – 1) = 3(x – 1)(x + 1)
4) 3ab² – 27a = 3a(b² – 9) = 3a(b – 3)(b + 3)
5) x3 – 4x = x(x² – 4) = x(x – 2)(x + 2)
6) 2y3 – 18y = 2y(y² – 9) = 2y(y – 3)(y + 3)
7) x4 – x² = x²(x² – 1) = x²(x – 1)(x + 1)
8) 0,09t4 – t6 = t4(0,09 – t2) = t4(0,3 – t)(0,3 + t)
9) 16/49 a2b4c5 – b2c3 = b2c3(16/49 a2b2c2 – 1) = b2c3(4/7 abc – 1)(4/7 abc + 1)
Завдання 787
1) 12b² – 12c² = 12(b² – c²) = 12(b – c)(b + c)
2) 2a²c – 2b²c = 2c(a² – b²) = 2c(a – b)(a + b)
3) 5a² – 20 = 5(a² – 4) = 5(a – 2)(a + 2)
4) 3mn² – 48m = 3m(n² – 16) = 3m(n – 4)(n + 4)
5) 7y^3 – 7y = 7y(y² – 1) = 7y(y – 1)(y + 1)
6) a3 – a5 = a3(1 – a2) = a3(1 – a)(1 + a)
Завдання 788 Розклад на множники
1) 9a²b² – 6ab² + b² = b² (9a² – 6a + 1) = b²(3a – 1)²
2) 4b²c – 20abc + 25a²c = c (4b² – 20ab + 25a²) = c(2b – 5a)²
3) –3m^3 + 6m²n – 3mn² = –3m (m² – 2mn + n²) = –3m(m – n)²
Завдання 789
1) 3a² + 6ab + 3b² = 3(a² + 2ab + b²) = 3(a + b)²
2) 5m² + 5n² – 10mn = 5(m² – 2mn + n²) = 5(m – n)²
3) –3x² + 12x – 12 = –3(x² – 4x + 4) = –3(x – 2)²
4) –7b² – 14bc – 7c² = –7(b² + 2bc + c²) = –7(b + c)²
5) x2y + 14xy2 + 49y3 = y(x2 + 14xy + 49y2) = y(x + 7y)2
6) –8a3b + 56a2b2 – 98ab3 = –2ab(4a2 – 28ab + 49b2) = –2ab(2a – 7b)²
Завдання 790
1) 8x² + 16xy + 8y² = 8(x² + 2xy + y²) = 8(x + y)²
2) –2a² + 24ab – 72b² = –2(a² – 12ab + 36b²) = –2(a – 6b)²
3) –12b^3 – 12b² – 3b = –3b(4b² + 4b + 1) = –3b(2b + 1)²
4) 48m^3n – 72m²n + 27mn = 3mn(16m² – 24m + 9) = 3mn(4m – 3)²
Завдання 791
1) a4 – 10 000 = (a2)2 – 1002 = (a2 – 100)(a2 + 100) = (a – 10)(a + 10)(a² + 100)
2) m8 – n4 = (m4)2 – (n2)2 = (m4 – n2)(m4 + n2) = (m² – n)(m² + n)(m^4 + n²)
Завдання 792
1) a4 – b4 = (a2 – b2)(a2 + b2) = (a – b)(a + b)(a2 + b2)
2) c4 – 81 = (c2 – 9)(c2 + 9) = (c – 3)(c + 3)(c2 + 9)
Завдання 793
1) x4 – 16 = (x² – 4)(x² + 4) = (x – 2)(x + 2)(x² + 4)
2) y8 – 1 = (y4 – 1)(y4 + 1) = (y2 – 1)(y2 + 1)(y4 + 1) = (y – 1)(y + 1)(y2 + 1)(y4 + 1)
Завдання 794
1) 16x – 2x4 = 2x (8 – x3) = 2x(8 – x3) = 2x(2 – x)(4 + 2x + x²)
2) 3a5 + 375a2 = 3a2(a3 + 125) = 3a2(a3 + 53) = 3a²(a + 5)(a² – 5a + 25)
Завдання 795
1) 4a3 – 4b3 = 4(a3 – b3) = 4(a – b)(a² + ab + b²)
2) 2m3 – 16 = 2(m3 – 8) = 2(m – 2)(m² + 2m + 4)
3) 7 + 7b3 = 7(1 + b3) = 7(1 + b)(1 – b + b2)
4) –x4 + 27x = –x(x3 – 27) = –x(x – 3)(x² + 3x + 9)
5) 2a4 – 250a = 2a(a3 – 125) = 2a(a – 5)(a² + 5a + 25)
6) 9a5 – 9a2 = 9a²(a3 – 1) = 9a²(a – 1)(a² + a + 1)
Завдання 796
1) 3x3 + 3y3 = 3(x3 + y3) = 3(x + y)(x² – xy + y²)
2) 5m4 – 320mn3 = 5m(m3 – 64n3) = 5m(m – 4n)(m² + 4m + 16n)
3) 6c5 – 6c8 = 6c5(1 – c^3) = 6c5(1 – c)(1 + c + c2)
Завдання 797
1) a7 + ab6 = a(a6 + b6) = a(a2 + b2)(a4 – a2b2 + b4)
2) x8 – y8 = (x4 – y4)(x4 + y4) = (x² – y²)(x² + y²)(x4 + y4) = (x – y)(x + y)(x² + y²)(x4 + y4)
3) c6 – 1 = (c2 – 1)(c4 + c2 + 1) = (c – 1)( c + 1)(c + 1)(c4 + c + 1)
Завдання 798
1) c6 + c9 = c6(1 + c3) = c6(1 + c)(1 – c + c2)
2) m9 – n9 = (m3 – n3)(m6 + m3n3 + n6)
3) a8 – b4 = (a4 – b2)(a4 + b2) = (a2 – b)(a2 + b)(a4 + b2)
Завдання 799
1) 3ab + 15b – 3a – 15 = (a + 5)(3b – 3)
2) 84 – 42y – 7xy + 14x = (2 – y)(42 + 7x)
3) abc + 6ac + 8ab + 48a = ac(b + 6) + 8a(b + 6) = (b + 6)(ac + 8a)
4) m3 – m2n + m2 – mn =m(m² – mn + m – n) = m(m(m – n) + (m – n)) = m(m – n)(m + 1)
5) a3 + a² – a – 1 = a²(a² – 1) – (a + 1) = (a + 1)(a² – 1) = (a + 1)(a – 1)(a + 1) = (a – 1)(a + 1)²
6) 2x3 – 2xy² – 8x² + 8y² = 2x(x² – y²) – 8(x² – y²) = (x² – y²)(2x – 8) = 2(x – y)(x + y)(x – 4)
7) 5a² – 5b² – 15a3b + 15ab3 = 5(a² – b²) – 15ab(a² – b²) = (a² – b²)(5 – 15ab) =
= 5(a – b)(a + b)(1 – 3ab)
8) a²b² – 1 – b² + a² = b²(a² – 1) + (a² – 1) = (a² – 1)(b² + 1) = (a – 1)(a + 1)(b² + 1)
Завдання 800
1) 15cx + 2cy – cxy – 30c = c(15x + 2y – xy – 30) = c((15x – 30) + (2y – xy)) =
= c(15(x – 2) – y(x – 2)) = c(x – 2)(15 – y)
2) 35a² – 42ab + 10a²b – 12ab² = 5a²(7 + 2b) – 6ab(7 + 2b) = (5a² – 6ab)(7 + 2b) =
= (a(5a – 6b))(7 + 2b)
3) x + x²y + x² + xy = x(x² + xy + x + y) = x(x(x + y) + (x + y)) = x(x + y)(x + 1)
4) mn4 – n4 + mn3 – n3 = n3(mn – n + m – 1) = n3(n(m – 1) + (m – 1) = n3(m – 1)(n + 1)
Завдання 801
1) (a² + b²)² – 4a²b² = ((a² + b²) – 2ab)((a² + b²) + 2ab) = (a² – 2ab + b²)(a² + 2ab + b²) =
= (a – b)²(a + b)²
2) 81 – (x² + 6x)² = (9 – (x² + 6x))(9 + (x² + 6x)) = (9 – x² – 6x)(9 + x² + 6x) =
= (9 – x² – 6x)(3 + x)²
Завдання 802
1) (m² – 2m)² – 1 = ((m² – 2m) – 1)((m² – 2m) + 1) = (m² – 2m – 1)(m² – 2m + 1) =
= (m² – 2m – 1)(m – 1)²
2) 16 – (m² + 4m)² = (4 – (m² + 4m))(4 + (m² + 4m)) = (4 – m² – 4m)(4 + m² + 4m) =
= (4 – m² – 4m)(2 + m)²
Завдання 803
1) x²(x – 2) – 18x(x – 2) + 81(x – 2) = (x² – 18x + 81)(x – 2) = (x – 9)²(x – 2)
2) 4x(y² – 9) + 4x²(y² – 9) – 9 + y² = 4x(y² – 9) + 4x²(y² – 9) + y² – 9 =
= (y² – 9)(4x + 4x² + 1) = (y – 3)(y + 3)(2x + 1)²
3) b²(a + 1) – a²(b + 1) = ab² + b² – a²b – a² = (ab² – a²b) + (b² – a²) =
= ab(b – a) + (b – a)(b + a) = = (b – a)(ab + b + a)
4) (a – b)(b² – c²) – (b – c)(a² – b²) = (a – b)(b – c)(b + c) – (b – c)(a – b)(a + b) =
= (a – b)(b – c)(b + c – a – b) = (a – b)(b – c)(c – a)
Завдання 804
1) x²(x + 4) – 20x(x + 4) + 100(x + 4) = (x² – 20x + 100)(x + 4) = (x – 10)²(x + 4)
2) a² – 36 – 2a(36 – a²) – a²(36 – a²) = a² – 36 – 72a + 2a3 – 36a² + a4 =
= a4 – 35a² – 72a – 36 = (a² – 36)(a² + 1) = (a – 6)(a + 6)(a² + 1)
3) a²(b – 1) – b²(a – 1) = a²b – a² – ab² + b² = (a²b – ab²) – (a² – b²) =
= ab(a – b) – (a – b)(a + b) = (a – b)(ab – a – b)
4) (m – n)(n3 – p3) – (n – p)(m3 – n3) =
= (m – n)(n – p)(n² + np + p²) – (n – p)(m – n)(m² + mn + n²) =
= (m – n)(n – p)(n² + np + p² – m² – mn – n²) = (m – n)(n – p)(np + p² – m² – mn) =
= (m – n)(n – p)((np – mn) + (p² – m²)) = (m – n)(n – p)(n(p – m) + (p – m)(p + m)) =
= (m – n)(n – p)(n + p + m)
Завдання 805 Рівняння
|
1) x3 – 4x = 0 x(x² – 4) = 0 x(x – 2)(x + 2) = 0 x = 0 або x – 2 = 0, або x + 2 = 0 x = 2 x = –2 |
5) x3 – 10x2 + 25x = 0 x(x² – 10x + 25) = 0 x(x – 5)² = 0 x = 0 або x – 5 = 0 x = 5 |
|
2) x4 – x² = 0 x²(x² – 1) = 0 x²(x – 1)(x + 1) = 0 x² = 0 або x – 1 = 0, або x + 1 = 0 x = 1 x = –1 |
6) x3 + 2x² – 9x – 18 = 0 (x3 – 9x) + (2x² – 18) = 0 x(x² – 9) + 2(x² – 9) = 0 (x + 2)(x² – 9) = 0 (x + 2)(x – 3)(x + 3) = 0 x + 2=0 або x – 3=0, або x + 3=0 x = –2 x = 3 x = –3 |
|
3) x5 – 36x3 = 0 x3(x2 – 36) = 0 x3(x – 6)(x + 6) = 0 x3 = 0 або x – 6 = 0 або x + 6 = 0 x = 0 х = 6 x = –6 |
7) x3 – 5x² + 4x – 20 = 0 x²(x – 5) + 4(x – 5) = 0 (x² + 4)(x – 5) = 0 x – 5 = 0 x = 5 |
|
4) 9x3 – x = 0 x(9x² – 1) = 0 x(3x – 1)(3x + 1) = 0 x = 0 або 3x – 1 = 0, або 3x + 1 = 0 x = 1/3 x = –1/3 |
8) x5 – x4 – x + 1 = 0 x4(x – 1) – 1(x – 1) = 0 (x4 – 1)(x – 1) = 0 (x² – 1)(x² + 1)(x – 1) = 0 (x – 1)(x + 1)(x² + 1)(x – 1) = 0 x = 1 x = –1 |
Завдання 806
|
1) x3 – x = 0 x(x² – 1) = 0 x(x – 1)(x + 1) = 0 x = 0 або x – 1 = 0, або x + 1 = 0 x = 1 x = –1 |
4) 49x^3 + 14x² + x = 0 x(49x² + 14x + 1) = 0 x(7x + 1)² = 0 x = 0 або 7x + 1 = 0 7х = –1 х = –1/7 |
|
2) x4 + x² = 0 x²(x² + 1) = 0 x² = 0 або x² + 1 = 0 x = 0 |
5) x3 + x² – x – 1 = 0 x²(x + 1) – (x + 1) = 0 (x + 1)(x² – 1) = 0 (x + 1)(x – 1)(x + 1) = 0 (x + 1) = 0 або (x – 1) = 0 x = –1 x = 1 |
|
3) x4 – 8x3 = 0 x3(x – 8) = 0 x3 = 0 або x – 8 = 0 x = 0 x = 8 |
6) x3 – 4x² – 25x + 100 = 0 x²(x – 4) – 25(x – 4) = 0 (x – 4)(x² – 25) = 0 (x – 4)(x – 5)(x + 5) = 0 x – 4=0 або x – 5=0 або x + 5=0 x = 4 x = 5 x = –5 |
Завдання 807 Тотожність
1) (a – 1)3 – 9(a – 1) = (a – 1)((a – 1)² – 9) = (a – 1)(a – 1 – 3)(a – 1 + 3) =
= (a – 1)(a – 4)(a + 2)
2) (x² +1)² – 4x² = (x² + 1 – 2x)(x² + 1 + 2x) = (x² – 2x + 1)(x² + 2x + 1) = (x – 1)²(x +1)²
Завдання 808
1) (a + 2)3 – 25(a + 2) = (a + 2)((a + 2)² – 25) = (a + 2)(a + 2 + 5)(a + 2 – 5) =
= (a + 2)(a + 7)(a – 3)
2) a² + 2ab + b² – c² + 2cd – d² = (a + b)² – (c – d)² = (a + b + c – d)(a + b – c + d)
Завдання 809 Розклад на множники двома способами:
а) застосуйте формулу різниці квадратів;
1) (ab + 1)² – (a + b)² = (ab + 1 – a – b)(ab + 1 + a + b) =
= (ab – a – b + 1)(ab + a + b + 1) = (a(b – 1) – (b – 1))((a(b + 1) + (b + 1)) =
= (b – 1)(a – 1)(b + 1)(a + 1)
2) a) (a + 2b)² – (ab + 2)² = ((a + 2b) – (ab + 2))((a + 2b) + (ab + 2)) =
= (a – ab + 2b – 2)(a + ab + 2b + 2)
б) розкрийте дужки та застосуйте метод групування:
1) (ab + 1)² – (a + b)² = a²b² + 2ab + 1 – a² – 2ab – b² = a²b² – a² – b² + 1 =
= a²(b² – 1) – (b² – 1) = (b² – 1)(a² – 1) = (b – 1)(b + 1)(a – 1)(a + 1)
2) (a + 2b)² – (ab + 2)² = a² + 4ab + 4b² – a²b² – 4ab – 4 = a² + 4b² –a²b² – 4 =
= a² – a²b² + 4b² – 4 = a²(1 – b²) – 4(1 – b²) = (1 – b²)(a² – 4) = (1 – b)(1 + b)(a – 2)(a + 2)
Завдання 810
1) a² + 2ab + b² – c² = (a + b)² – c² = (a + b – c)(a + b + c)
2) c² + 4c + 4 – k² = (c + 2)² – k² = (c + 2 – k)(c + 2 + k)
3) 9a² + c² + 6ac – 9 = (3a + c)² – 9 = (3a + c – 3)(3a + c + 3)
4) a² – b² – 10b – 25 = a² – (b² + 10b + 25) = a² – (b + 5)² = (a – b – 5)(a + b + 5)
5) 49 – y² + x² – 14x = (x² – 14x + 49) – y² = (x – 7)² – y² = (x – 7 – y)(x – 7 + y)
6) mn² – m^3 – 12m² – 36m = m(n² – m² – 12m – 36) = m(n² – (m² + 12m + 36)) =
= m(n² – (m + 6)²) = m(n – m + 6)(n + m + 6)
Завдання 811
Подайте у вигляді добутку вираз:
1) x² – 18xy + 81y² – z² = (x – 9y)² – z² = (x – 9y – z)(x – 9y + z)
2) 64x² + 48xy + 9y² – 144 = (8x + 3y)² – 144 = (8x + 3y – 12)(8x + 3y + 12)
3) c² – a² + 22a – 121 = c² – (a² – 22a + 121) = c² – (a – 11)² = (c – (a – 11))(c + (a – 11))
4) 100 – 25y2 – 60x2y – 36x4 = 100 – (25y2 + 60x2y + 36x4) = 100 – (5y + 6x)2 =
= (10 – 5y – 6x)(10 + 5y + 6x
Завдання 812
1) a² – b² – a – b = (a – b)(a + b) – (a + b) = (a + b)(a – b – 1)
2) x – y – x² + y² = x – y – (x² – y²) = x – y – (x – y)(x + y) = (x – y)(1 – x – y)
3) 4m² – 9n² + 2m + 3n = (2m – 3n)(2m + 3m) + 2m + 3n = (2m + 3n)(2m – 3n + 1)
4) c² – d² + 4c – 4d = (c + d)(c – d) + 4(c – d) = (c – d)(c + d + 4)
5) 5x²y – 5xy² – x² + y² = 5xy(x – y) – (x – y)(x + y) = (x – y)(5xy – (x + y)) =
= (x – y)(5xy – x – y)
6) a² – 10a + 25 – ab + 5b = (a² – 10a + 25) – (ab – 5b) = (a – 5)² – b(a – 5) =
= (a – 5)(a – 5 – b)
7) 8mp + 8np – m² – 2mn – n² = 8p(m + n) – (m² + 2mn + n²) = 8p(m + n) – (m + n)² =
= (m + n)(8p – m – n)
8) a3 + b3 – a2b – ab2 = (a + b)(a2 – ab + b2) – ab(a + b) = (a + b)(a2 – ab + b2 – ab) =
= (a + b)(a² – 2ab + b²) = (a + b)(a – b)²
9) m3 – 8n3 – m2 + 4mn – 4n2 = (m – 2n)(m2 + 4mn + 4n2) – (m2 – 4mn + 4n2)
10) a3 – 4a2 + 4a – 1 = (a – 1)(a2 + a + 1) – 4a(a – 1) = (a – 1)(a2 + a + 1 – 4a) =
= (a – 1)(a2 – 3a + 1)
Завдання 813
1) m² – n² – m + n = (m – n)(m + n) – (m – n) = (m – n)(m + n – 1)
2) c + d – c² + d² = (c + d) – (c² – d²) = (c + d) – (c – d)(c + d) = (c + d)(1 – c + d)
3) 16x² – 25y² – 4x – 5y = (4x – 5y)(4x + 5y) – (4x + 5y) = (4x + 5y)(4x – 5y – 1)
4) 12a2b3 + 3a3b2 + 16b2 – a2 = 3a²b²(4b + a) + (4b – a)(4b + a)
5) 49c² – 14c + 1 – 21ac + 3a = (49c² – 14c + 1) – 21ac + 3a = (7c – 1)² – 3a(7c – 1) =
= (7c – 1)(7c – 1 – 3a)
6) ax2 + ay2 + x4 + 2x2y2 + y4 = a(x2 + y2) + (x2 + y2)2 = (x² + y²)(a + x² + y²)
7) 27c3 – d3 + 9c2 + 3cd + d2 = (27c3 – d3) + (9c2 + 3cd + d2) =
= (3c – d)(9c² + 3cd + d²) + (9c² + 3cd + d²) = (3c – d)(9c² + 3cd + d²)
8) b3 – 2b2 – 2b + 1 = (b + 1)(b2 – b + 1) – 2b(b + 1) = (b + 1)(b2 – b + 1 – 2b) =
= (b + 1)(b2 – 3b + 1)
Завдання 814 Куб двочлена
1) a3 + 3a2 + 3a + 1 = (a3 + 1)(3a2 + 3a) = (a + 1)(a2 – a + 1) + 3a(a + 1) =
= (a + 1)(a² – a + 1 + 3a) = (a + 1)(a² + 2a + 1) = (a + 1)(a + 1)² = (a + 1)3
2) b3 – 6b2 + 12b – 8 = (b3 – 8) – (6b2 – 12b) = (b – 2)(b2 + 2b + 4) – 6b(b – 2) =
= (b – 2)(b² + 2b + 4 – 6b) = (b – 2)(b² – 4b + 4) = (b – 2)(b – 2)² = (b – 2)3
Завдання 815 Тотожність
1) (a + b + c)3 – a3 – b3 – c3 = 3(a + b)(b + c)(a + c);
(a + b + c)3 – a3 – b3 – c3 = ((a + b + c)3 – a3 – (b3 + c3) =
= (a + b + c – a)((a + b + c)² + (a + b + c)a + a²) – (b + c)(b² – bc + c²) =
= (b + c)(a² + b² + c² + 2ab + 2ac + 2bc + a² + ab + ac + a²) – (b + c)(b² – bc + c²) =
= (b + c)(a² + b² + c² + 2ab + 2ac + 2bc + a² + ab + ac + a² – b² + bc – c²) =
= (b + c)(3a^3 + 3ab + 3ac + 3bc) = 3(b + c)(a² + ab + ac + bc) =
= 3(b + c)(a(a + b) + c(a + b)) = 3(a + b)(b + c)(a + c)
2) (a – b)3 + (b – c)3 – (a – c)3 = –3(a – b)(b – c)(a – c).
(a – b)3 + (b – c)3 – (a – c)3 =
= (a – b + b – c)((a – b)2 – (a – b)(b – c) + (b – c)2) – (a – c)3 =
= (a – c)((a – b)2 – (a – b)(b – c) + (b – c)2) – (a – c)3 =
= (a – c)((a – b)2 – (a – b)(b – c) + (b – c)2 – (a – c)2) =
=(a – c)(a² – 2ab + b² – ab + ac + b² – bc + b² – 2bc + c² – a² + 2ac – c²) =
= (a – c)(–3ab + 3b² + 3ac – 3bc) = (a – c)(–3b(a – b) + 3c(a – b)) =
= (a – c)(a – b)(–3b + 3c) = –3(a – b)(b – c)(a – c)
Завдання 816 Розклад на множники
1) (x – y) (x + y) + 2 (x + 3y) – 8 = x² – y² + 2x + 6y – 8 = (x² + 2x + 1) – (y² – 6y + 9) =
= (x + 1)² – (y – 3)² = (x + 1 – y + 3)(x + 1 + y – 3) = (x – y + 4)(x + y – 2)
2) (2a – 3b) (2a + 3b) – 4 (a + 3b) – 3 = 4a² – 9b² – 4a – 12b – 3 =
= (4a² – 4a + 1) – (9b² + 12b + 4) = (2a – 1)² – (3b + 2)² =
= (2a – 1 – 3b – 2)(2a – 1 + 3b + 2) = (2a – 3b – 3)(2a + 3b + 1)
Завдання 817 Вираз у вигляді добутку
1) (5x – y2) (5x + y2) – 2 (15x – 7y2) – 40 = 25x2 – y4 – 30x + 14y2 – 40 =
= (25x2 – 30x + 9) – (y4 – 14y2 + 49) = (5x – 3)2 – (y2 – 7)2 =
= (5x – 3 – y² + 7)(5x – 3 + y² – 7) = (5x – y² + 4)(5x + y² – 10)
2) (3m – 2n)(12m + 5n) + 3m(3n + 4) – 2(3n² – 20n +12) =
= 36m² + 15mn – 24mn – 10n² + 9mn + 12m – 6n² + 40n – 24 =
= 36m² – 16n² + 12m + 40n – 24 = (36m² + 12m + 1) – (16n² – 40n + 25) =
= (6m + 1)² – (4n – 5)² = (6m + 1 – 4n + 5)(6m + 1 + 4n – 5) =
= (6m – 4n + 6)(6m + 4n – 4) = 4(3m – 2n + 3)(3m + 2n – 2)
Завдання 818
Розкладіть на множники тричлен, виділивши попередньо квадрат двочлена:
1) x² – 10x + 24 = (x² – 10x + 25) – 1 = (x – 5)² – 1 = (x – 5 – 1)(x – 5 + 1) = (x – 6)(x – 4)
2) a² + 4a – 32 = (a² + 4a + 4) – 36 = (a + 2)² – 36 = (a + 2 – 6)(a + 2 + 6) = (a – 4)(a + 8)
3) b² – 3b – 4 = (b² – 3b + 2,25) – 6,25 = (b – 1,5)² – 6,25 = (b – 1,5 – 2,25)(b – 1,5 + 2,25) =
= (b – 3,75)(b + 3,75)
4) 4a² – 12a + 5 = (4a² – 12a + 9) – 4 = (2a – 3)² – 4 = (2a – 3 – 2)(2a – 3 + 2) =
= (2a – 5)(2a – 1)
5) 9x² – 24xy + 7y² = (9x² – 24xy + 16y²) – 9y² = (3x – 4y)² – (3y)² =
= (3x – 4y – 3y)(3x – 4y + 3y) = (3x – 7y)(3x – y)
6) 36m² – 60mn + 21n² = (36m² – 60mn + 25n²) – 4n² = (6m – 5n)² – (2n)² =
= (6m – 5n – 2n)(6m – 5n + 2n) = (6m – 7n)(6m – 3n) = 3(6m – 7n)(2m – n)
Завдання 819
|
1) x² – 4x + 3 = (x – 3)(x – 1) 2) a² + 2a – 24 = (a + 6)(a – 4) 3) y² + 12y + 35 = (y + 7)(y + 5) |
4) x² + x – 6 = (x + 3)(x – 2) 5) c² + 8cd + 15d² = (c + 3d)(c + 5d) 6) 9x² – 30xy + 16y² = (3x – 8y)(3x – 2y) |
Завдання 820
Значення змінних x1 і x2 є такими, що виконуються рівності x1 – x2 = 8, x1x2 = 5. Знайдіть значення виразу:
1) x1x2² – x1²x2 = x1x2(x2 – x1) = –x1x2(x1 – x2) = –5 • (8) = –40
2) x1² + x2² = x1² – 2x1x2 + x2² + 2x1x2 = (x1 – x2)² + 2x1x2 = 8² + 2 • 5 = 74
3) (x1 + x2)² = x1² + 2x1x2 + x2² = x1² – 2x1x2 + x2² + 4x1x2 = (x1 – x2)² + 4x1x2 = 8² + 4 • 5 = 84
4) x13 – x23 = (x1 – x2)(x1² + x1x2 + x2²) = (x1 – x2)((x1² – 2x1x2 + x2²) + 3x1x2) =
= (x1 – x2)((x1 – x2)² + 3x1x2) = 8 • (8² + 3 • 5) = 8 • 79 = 632
Завдання 821
Значення змінних x і у є такими, що виконуються рівності x + у = 6, xy = –3. Знайдіть значення виразу:
1) x3y2 + x2y3 = x2y2(x + y) = (xy)2(x + y) = (–3)2 • 6 = 9 • 6 = 54
2) (x – y)² = x² – 2xy + y² = (x² + 2xy + y²) – 2xy – 2xy = (x + y)² – 4xy = 6² – 4 • (–3) =
= 36 + 12 = 48
3) x4 + y4 = (x4 + 2x2y2 + y4) – 2x2y2 = (x² + y²)² – 2x²y² = ((x² + 2xy + y²) – 2xy)² – 2x²y² =
= ((x + y)² – 2xy)² – 2(xy)² = ((6² – 2 • (–3))² – 2 • (–3)² = (36 + 6)² – 2 • 9 = 42² – 18 =
= 1764 – 18 = 1746
Завдання 822
Доведіть, що при будь–якому натуральному n значення виразу (2n – 1)3 – 4n2 + 2n +1 ділиться націло на 16.
(2n – 1)3 – 4n2 + 2n + 1 = (2n – 1)(2n – 1)2 – 4n2 + 2n + 1 =
= (2n – 1)(4n² – 4n + 1) – 4n² + 2n + 1 = 8n3 – 8n2 + 2n – 4n2 + 4n – 1 – 4n2 + 2n + 1 =
= 8n3 – 16n2 + 8n = 8n(n2 – 2n + 1) = 8n(n – 1)2 ділиться на 8, із його двох послідовних натуральних множників n і n – 1 один завжди ділиться на 2.
Завдання 823
1) x4 – 5x2 + 4 = (x2 – 4)(x2 – 1) = (x – 2)(x + 2)(x – 1)(x + 1)
2) x4 + x2 + 1 = (x2 + x + 1)(x2 – x + 1)
3) 4x4 – 12x2 + 1 = (4x4 + 4x2 + 1) – 16x2 = (2x2 + 1)2 – (4x)2 = (2x2 + 1 – 4x)(2x2 + 1 + 4x)
4) x5 + x + 1 = (x5 – x2) + (x2 + x + 1) = x2(x3 – 1) + (x2 + x + 1) =
= x2(x – 1)(x2 + x + 1) + (x2 + x + 1) = (x2 + x + 1)(x3 – x2 + 1)
5) x4 + 4 = (x4 + 4x2 + 4) – 4x2 = (x2 + 2)2 – (2x)2 = (x² + 2 – 2x)(x² + 2 + 2x)
6) x8 + x4 – 2 = (x8 – 1) + (x4 – 1) = (x4 – 1)(x4 + 1) + (x4 – 1) = (x4 – 1)(x4 + 1 + 1) =
= (x4 – 1)(x4 + 2) = (x2 – 1)(x2 + 1)(x4 + 2) = (x – 1)(x + 1)(x2 + 1)(x4 + 2)
Завдання 824
1) x4 + 5x2 + 9 = (x4 + 6x2 + 9) – x2 = (x2 + 3)2 – x2 = (x2 + 3 – x)(x2 + 3 + x)
2) x4 – 8x2 + 4 = (x4 – 4x2 + 4) – 4x2 = (x2 – 2)2 – 4x² = (x² – 2 – 2x)(x² – 2 + 2x)
Завдання 825
Доведіть, що при будь–якому натуральному значенні n, відмінному від 1, значення виразу n^4 + n² + 1 є складеним числом.
n4 + n2 + 1 = (n4 + 2n2 + 1) – n2 = (n2 + 1)2 – n2 = (n2 + 1 – n)(n2 + 1 + n) – при будь–якому натуральному значення n, відмінному від 1, значення виразу n4 + n2 + 1 є складеним числом.
ВПРАВИ ДЛЯ ПОВТОРЕННЯ
Завдання 826
Під час оплати послуг через платіжний термінал стягується комісія в розмірі 3 %. Термінал приймає суми, кратні 10 грн. Ганна хоче поповнити рахунок свого мобільного телефону не менше ніж на 200 грн. Яку найменшу суму грошей вона має заплатити через цей термінал?
Розв'язання
200 + 200 • 0,03 = 206 (грн) – потрібно хлопцю, щоб на рахунку було 200 грн;
За умовою термінал приймає суми кратні 10 грн, тобто йому потрібно не менше 210 грн, тоді на рахунку в нього буде:
210 : 1,03 = 203,88 (грн).
Відповідь: 203, 88 грн.
Завдання 827
Дано три числа, з яких кожне наступне на 4 більше за попереднє. Знайдіть ці числа, якщо добуток меншого й більшого з них на 88 менший від добутку більшого й середнього.
Розв'язання
Нехай друге число дорівнює х, тоді перше число – (х – 4), а третє – (х + 4). Складаємо рівняння:
(х – 4)(x + 4) + 88 = х(х + 4)
x² – 16 + 88 = х² + 4х
4х =72
х = 18 – друге число;
18 – 4 = 14 – перше число;
18 + 4 = 22 – третє число.
Відповідь: 14, 18, 22.
Завдання 828
Петро піднявся на гору зі швидкістю 2,5 км/год, а потім спустився іншою дорогою зі швидкістю 4 км/год. Знайдіть загальний шлях, пройдений Петром, якщо дорога на гору на 3 км коротша від дороги з гори, а час, витрачений на весь шлях, становить 4 год.
Розв'язання
Нехай довжина дороги на гору дорівнює х км, тоді довжина дороги з гори – (х + 3) км. Час підйому на гору дорівнює х/2,5 год, а час спуску з гори – (х + 3)/4 год. Складаємо рівняння:
x/2,5 + (x + 3)/4 = 4
(4x + 2,5(x + 3))/10 = 4
4х + 2,5x + 7,5 = 40
6,5х = 32,5
x = 5 (км) – довжина дороги на гору;
5 + 3 = 8 (км) – довжина спуску з гори;
5 + 8 = 13 (км) – весь шлях Петра.
Відповідь: 13 км.
Завдання 829 Рівняння
|
1) |7x – 3| = 4 7x – 3 = 4 або 7x – 3 = –4 7x = 7 або 7x = –1 x = 1 x = 1/7 |
2) || x | – 10 | = 8 |x| – 10 = 8 або |x| – 10 = –8 |x| = 18 |x| = 2 x = 18 або x = –18 x = 2 або x = –2 |
|
3) 4 (x – 2) + 5 | x | = 10 а) Нехай x ≥ 0. Маємо 4(x – 2) + 5x = 10 4x – 8 + 5x = 10 9x = 18 x = 2 б) Нехай x < 0. Маємо 4(x – 2) – 5x = 10 4x – 8 – 5x = 10 –x = 18 x = –18 |
4) | x | = 3x – 8; а) Нехай x ≥ 0. Маємо: x = 3x – 8 x – 3x = –8 –2x = –8 x = 4 б) Нехай x < 0. Маємо: –x = 3x – 8 –x – 3x = –8 –4x = –8 x = 2 – не підходить. |
Завдання 830
Доведіть, що сума трицифрового числа та подвоєної суми його цифр ділиться націло на 3.
Подамо трицифрове число у вигляді xyz = 100х + 10у + z, де х, у, z – деякі цифри.
Маємо: 100х + 10у + z + 2(х + у + z) = 102х + 12у + 3z. Оскільки кожен із трьох отриманих доданків ділиться націло на 3, то і згадана в задачі сума ділиться націло на 3.
ГОТУЄМОСЯ ДО ВИВЧЕННЯ НОВОЇ ТЕМИ
Завдання 831
Обчисліть значення у за формулою у = 0,2x – 3, якщо:
1) Якщо х = 4, тоді у = 0,2х – 3 = 0,2 • 4 – 3 = 0,8 – 3 = –2,2
2) якщо х = –3, тоді у = 0,2х – 3 = 0,2 • (–3) – 3 = –0,6 – 3 = –3,6
Завдання 833
На координатній площині позначте точки: A (2; 3); B(4; 5); C(–3; 7); D(–2; 2); K(–2; –2); M(0; 2); N(–3; 0); P(1; –6); F(–4; –2).
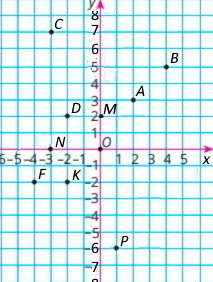
Завдання 834
Побудуйте відрізки AB і CD та знайдіть координати точки перетину цих відрізків, якщо A(–5; –2); B(1; 4); C(–3; 2); D(2;–3).
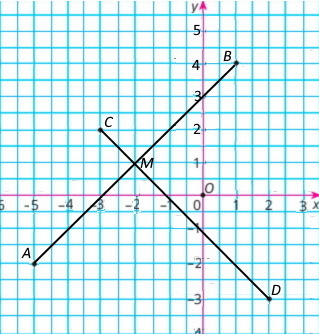
M(–2; 1) – точка перетину відрізків АВ і CD.
Завдання 835
Як розміщена на координатній площині відносно осі x точка:
|
1) A (2; 6); Над віссю х 2) B(–3; 1); Над віссю х |
3) C(–4; –5); Під віссю х 4) D(–3; 0)? На осі х |
Завдання 836
Знайдіть координати вершин квадрата зі стороною 4, якщо дві його сторони лежать на осях координат, а добуток координат однієї з вершин – додатне число. Скільки розв’язків має задача?
|
Перший розв'язок |
Другий розв'язок |
|
|
|
|
1) А(0;0); В(0;4); С(4;4); D(4;0), бо 4 • 4 = 16, а 16 > 0 |
2) А(0;0); В(0;–4); С(–4;–4); D(–4;0), бо –4 • (–4) = 16, а 16 > 0 |
УЧИМОСЯ РОБИТИ НЕСТАНДАРТНІ КРОКИ
Завдання 837
Нехай x1, x2, ..., x25 – деякий набір натуральних чисел, а набір y1, y2, ..., y25 отримано з нього в результаті перестановки деяких чисел. Доведіть, що значення виразу (x1 – y1)(x2 – y2)...(x25 –y25) є парним числом.
Міркуємо так. Якщо б отриманий добуток був непарним числом, то тоді кожен із n множників (х1 – у1), (х2 – у2), .... (х25 – у25) – теж був би непарним. Тоді в цих множниках було б одне з чисел обов'язково парне, а інше обов'язково непарне. Але оскільки кількість чисел у наборі непарна, то неможливо переставити усі парні числа на місяця непарних чи навпаки. Тому отриманий добуток має бути парним числом.