Завдання 1320
Доведіть, що при будь–якому натуральному значенні n значення виразу дорівнює квадрату деякого натурального числа.
n(n + 2)(n + 4)(n + 6) + 16 = (n(n + 6) • (n + 2)(n + 4)) + 16 =
= (n² + 6n)(n² + 4n + 2n + 8) + 16 = (n² + 6n)(n² + 6n + 8) + 16 =
= (n² + 6n + 4 – 4)(n² + 6n + 4 + 4) + 16 = (n² + 6n + 4)² – 4² + 16 =
= (n² + 6n + 4)² – 16 + 16 = (n² + 6n + 4)²
Завдання 1321
Доведіть, що різниця між квадратом натурального числа, яке не кратне 3, і числом 1 кратна 3.
Натуральне число x, яке не кратне 3 можна записати х = 3n + 1 або х = 3n + 2.
Якщо х = 3n + 1, то (3n + 1)² – 1 = 9n² + 6n + 1 – 1 = 9n² + 6n = 3(3n² + 2n) — кратне 3.
Якщо х = 3n + 2, то (3n + 2)² – 1 = 9n² + 12n + 4 – 1 = 9n² + 12n + 3 = = 3(3n² + 4n + 1)
— кратне 3.
Завдання 1322
Доведіть, що при будь–якому натуральному значенні n, яке не кратне 5, значення виразу n4 – 1 ділиться націло на 5
n4 – 1 = (n²)² – (1²) = (n² – 1)(n² + 1) = (n² – 1²)(n² + 1) = (n – 1)(n + 1)(n² + 1)
Натуральне число n, яке не кратне 5 можна записати n = 5m + 1, n = 5m + 2, n = 5m + 3, n = 5m + 4
Якщо n = 5m + 1, тоді
n4 – 1 = (5m + 1 – 1)(5m + 1 + 1)((5m + 1)²+1) = 5m(5m + 2)((5m + 1)²+1) — кратне 5.
Якщо n = 5m + 2, тоді
n4 – 1 = (5m + 2 – 1)(5m + 2 + 1)((5m + 2)² + 1) = (5m + 1)(5m + 3)((5m + 2)² + 1) =
= (5m + 1)(5m + 3)(25m² + 20m + 4 + 1) = (5m + 1)(5m + 3)(25m² + 20m + 5) =
= 5(5m + 1)(5m + 3)(5m² + 4m + 1) — кратне 5.
Якщо n = 5m + 3, тоді
n4 – 1 = (5m + 3 – 1)(5m + 3 + 1)((5m + 3)² + 1) = (5m + 2)(5m + 4)((5m + 3)² + 1) =
= (5m + 2)(5m + 4)(25m² + 30m + 9 + 1) = (5m + 1)(5m + 3)(25m² + 30m + 10) =
= 5(5m + 1)(5m + 3)(5m² + 6m + 2) — кратне 5.
Якщо n = 5m + 4, тоді
n4 – 1 = (5m + 4 – 1)(5m + 4 + 1)((5m + 4)² + 1) = (5m + 3)(5m + 5)((5m + 4)² + 1) =
= 5(5m + 3)(m + 1)((5m + 4)² + 1) — кратне 5.
Завдання 1323
Чи можна стверджувати, що значення виразу n3 + 2n ділиться націло на 3 при будь–якому натуральному значенні n?
n3 + 2n = n(n² + 2)
Натуральне число n, яке ділиться націло на 3 можна записати n = 3m
Якщо n = 3m, тоді n3 + 2n = 3m((3m)2 + 2) = 3m(9m2 + 2) — кратне 3.
Натуральне число n, яке не ділиться націло на 3 можна записати n = 3m + 1, n = 3m + 2
Якщо n = 3m + 1, тоді n3 + 2n = (3m + 1)((3m + 1)2 + 2) = (3m + 1)(9m² + 6m + 1 + 2) =
= (3m + 1)(9m² + 6m + 3) = 3(3m + 1)(3m² + 2m + 1) — кратне 3.
Якщо n = 3m + 2, тоді n3 + 2n = (3m + 2)((3m + 2)2 + 2) = (3m + 2)(9m2 + 12m + 4 + 2)=
= (3m + 2)(9m2 + 12m + 6) = 3(3m + 2)(3m2 + 4m + 2) — кратне 3.
Завдання 1324
Доведіть, що при будь–якому натуральному значенні n значення виразу n7−n кратне 42.
n7 – n = n(n6 – 1) = n(n3 – 1)(n3 + 1) = n(n – 1)(n² + n + 1)(n + 1)(n² – n + 1) =
= n(n – 1)(n + 1)(n² – n + 1)(n² + n + 1).
Із трьох послідовних натуральних чисел n – 1, n і n + 1 одне обов’язково ділиться на 2 і одне — на 3, тому значення виразу при будь–якому натуральному значенні n ділиться на 6 (2 • 3 = 6). Залишилося показати, що воно ділиться на 7 (42 : 6 = 7).
Натуральне число n, яке не є кратне 7 можна записати n = 7m + 1, n = 7m + 2, n = 7m + 3, n = 7m + 4, n = 7m + 5, n = 7m + 6
Якщо n = 7m + 1, тоді n – 1 = (7m + 1 – 1) = 7m — кратне 7.
Якщо n = 7m + 2, тоді (n² + n + 1) = (7m + 2)² + (7m + 2) + 1 =
= (49m² + 28m + 4) + 7m + 3 = 49m² + 35m + 7 = 7(7m² + 5m + 1) — кратне 7.
Якщо n = 7m + 3, тоді (n² – n + 1) = (7m + 3)² – (7m + 3) + 1 =
= (49m² + 42m + 9) – 7m – 2 = 49m² + 35m + 7 = 7(7m² + 5m + 1) — кратне 7.
Якщо n = 7m + 4, тоді (n² + n + 1) = (7m + 4)² + (7m + 4) + 1 =
= (49m² + 56m + 16) + 7m + 5 = 49m² + 63m + 21 = 7(7m² + 9m + 3) — кратне 7.
Якщо n = 7m + 5, тоді (n² – n + 1) = (7m + 5)² – (7m + 5) + 1 =
= (49m² + 70m + 25) – 7m – 4 = 49m² + 63m + 21 = 7(7m² + 9m + 3) — кратне 7.
Якщо n = 7m + 6, тоді n + 1 = (7m + 6 + 1) = 7m + 7 = 7(m + 1) — кратне 7.
Завдання 1325 Порівняйте функції
|
ƒ(х) = х² – 2х і g(х) = (х – 2)/х |
||
|
1) ƒ(2) = 2² – 2 • 2 = 0 g(–1) = (–1 – 2)/(–1) = 3 0 < 3 ƒ(2) < g(–1) |
2) ƒ(0) = 02 – 2 • 0 = 0 g(0) = (2 – 2)/2 = 0 0 = 0 ƒ(0) = g(2) |
3) ƒ(1) = 12 – 2 • 1 = –1 g(1) = (1 – 2)/1 = –1 –1 = –1 ƒ(1) = g(1) |
Завдання 1326
Задамо функцію описом: кожному із значень аргументу –3, –1, 1, 3, 5 відповідає значення функції на 2 менше від відповідного значення аргументу.
Задамо функцію формулою: у = х – 2, де х = –3, –1, 1, 3, 5.
Завдання 1327
При всіх додатних значеннях аргументу значення функції ƒ дорівнює –1, при всіх від’ємних — дорівнює 1, а ƒ (0) = 0. Побудуйте графік функції ƒ.
|
у = –1, якщо х > 0 у = 0, якщо х = 0 у = 1, якщо х < 0 |
|
Завдання 1328
Знайдіть координати точки графіка функції y = 6x – 5:
|
1) абсциса й ордината рівні (х = у); х = 6х – 5 –5х = –5 х = 1 у = 1 Координати точки (1; 1) |
2) сума координат якої дорівнює 30. х + у = 30 х = 30 – у Підставимо в рівняння у = 6х – 5: у = 6(30 – у) – 5 у = 180 – 6у – 5 7у = 175 у = 25 х = 30 – 25 = 5 Координати точки (5; 25) |
Завдання 1329
При якому значенні a через точку M (3;–2) проходить графік функції:
|
1) у = ах – 8; –2 = 3а – 8 За = 6 а = 2 |
2) у = 1/3х – а. –2 = 1/3 • 3 – а –2 = 1 – а а = 3 |
Завдання 1330 Лінійна функція
|
1) ƒ(x) = (x – 1)(x + 1) – х(х – 3); ƒ(x) = х² – 1 – x² + x; ƒ(x) = x – 1 – функція є лінійною.
|
|
||||||
|
2) ƒ(x) = (2х – 3)² – (х + 4) (х – 2); ƒ(x) = 4х² – 12x + 9 – x² + 2x – 4x + 8; ƒ(x) = 3x² – 14х + 17 — функція не є лінійною. |
|||||||
|
3) ƒ(х) = (х + 3)² – х(х + 6); ƒ(х) = х² + 6х + 9 – х² – 6х; ƒ(х) = 9 — функція є лінійною. |
 |
||||||
Завдання 1331
Графіки функцій y = (5 – a) x + a і y = ax + 2 перетинаються в точці, абсциса якої дорівнює –3. Знайдіть ординату цієї точки.
За умовою графіки перетинаються, тому
(5 – a)x + a = ax + 2
5х – ах + а = ах + 2
5х – ах + а – ах = 2
5х – 2ах + а = 2
Якщо х = –3, тоді
5 • (–3) – 2а • (–3) + а = 2
–15 + 6а + а = 2
7а = 17
а = 17/7
Підставимо х = –3 і а = 17/7 в рівняння y = ах + 2, одержимо:
y = 17/7 • (–3) + 2 = –51/7 + 2 = –7 2/7 + 2 = –5 2/7
Завдання 1332
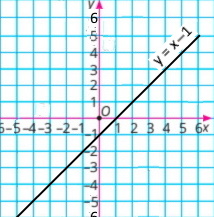
|
y = 2x + 3
|
|
Користуючись графіком, знайдіть значення аргументу, при яких значення функції:
1) дорівнює 5, якщо х = 1;
2) більше за 5, якщо х > 1;
3) менше від 5, якщо x < 1;
4) більше за –3, але менше від 7, якщо –3 < х < 2.
Завдання 1333
Не виконуючи побудови графіка функції y = 12x – 6, знайдіть координати:
1) точок перетину графіка з осями координат;
З віссю абсиц (х = 0): у = 12 • 0 – 6 = –6, координати точки (0;–6)
З віссю ординат (у = 0): 0 = 12х – 6; 12х = 6; х = 0,5, координати точки (0,5;0)
2) точки перетину графіка y = 12x – 6 з графіком функції у = 6х + 24.
Графіки перетинаються, тому
12x – 6 = 6х + 24
12х – 6х = 24 + 6
6х = 30
х = 5
Підставимо знайдене значення в рівняння y = 12x – 6:
y = 12 • 5 – 6 = 54
Отже, графіки перетинаються в точці з координатами (5;54).
Завдання 1334 Побудова графіка функціїї
|
у = |х| – 3 |
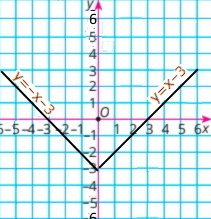
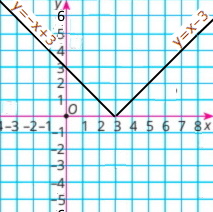
2) у = |х – 3| |
||||||||||||||||||||||||||
|
Якщо х ≥ 0, то у = х – 3
|
Якщо x < 0, то у = –х – 3
|
Якщо х ≥ 3, то y = x – 3
|
Якщо х < 3, то у = –x + 3
|
||||||||||||||||||||||||
|
|
 |
||||||||||||||||||||||||||
Завдання 1335
При якому значенні a пара (a;–a) є розв’язком рівняння:
|
1) 6х + 5у = 7; 6а + 5(–а) = 7 а = 7 |
2) 8х – 2у – 4; 8а – 2(–а) = 4 10а = 4 а = 0,4 |
3) х² – 3у = 0; а² – 3(–а) = 0 а² + 3а = 0 а(а + 3) = 0 а = 0 або а + 3 = 0 а = –3 |
4) х + |у| = –2. а + |–а|=–2 Нехай а < 0, тоді а – а = –2 0а = –2, коренів немає. Нехай а ≥ 0, тоді а + а = –2 2а = –2 a = –1, за умовою а > 0, коренів немає. Отже, при жодному а. |
Завдання 1336
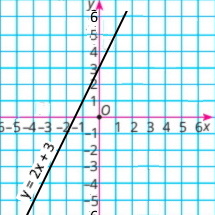
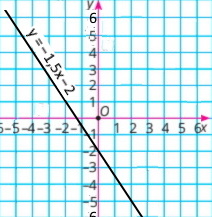
Побудуйте графік рівняння y + 1,5x = c, якщо він проходить через точку A(–2;1).
1 + 1,5 • (–2) = с
с = –2, тому рівняння має вигляд: у + 1,5х = –2
|
y = –1,5x – 2
|
|
Завдання 1337
Складіть систему двох лінійних рівнянь із двома змінними, розв’язком якої є пара чисел:
|
1) абсциса й ордината рівні (х = у); х = 6х – 5 –5х = –5 х = 1 у = 1 Координати точки (1; 1) |
2) сума координат якої дорівнює 30. х + у = 30 х = 30 – у Підставимо в рівняння у = 6х – 5: у = 6(30 – у) – 5 у = 180 – 6у – 5 7у = 175 у = 25 х = 30 – 25 = 5 Координати точки (5; 25) |
Завдання 1329
1) (1;1);
Підставимо (1;1) у формулу y = kx + b, отримаємо: 1 = k + b
Якщо k = 2, то 1 = 2 + b; b = –1, рівняння має вигляд: у = 2х – 1
Якщо k = 3, то 1 = 3 + b; b = –2, рівняння має вигляд: у = 3х – 2
Маємо систему двох лінійних рівнянь з двома змінними:
{2х – у = 1
3х – y = 2
2) (–3;5).
Підставимо (–3;5) у формулу y = kx + b, отримаємо: 5 = –3k + b
Якщо k = 1, то 5 = –3 + b; b = 8, рівняння має вигляд: у = х + 8
Якщо k = 2, то 5 = –6 + b; b = 11, рівняння має вигляд: у = 2х + 11
Маємо систему двох лінійних рівнянь з двома змінними:
{x – y = –8
2x – y = –11
Завдання 1338 Розв’язування системи рівнянь
|
1) {3x + 7у = 1 |•5 6у – 5x = 16 |•3 {15x + 35y = 5 –15x + 18y = 48 53y = 53 y = 1 Підставляємо в рівняння 3x + 7y = 1: 3x + 7 = 1 3х = –6 x = –2 Відповідь: (–2;1) |
2) {3x – 5у = 19 |•(–2) 2x + 3у = 0 |•3 {–6x + 10y = –38 6x + 9y = 0 19y = –38 y = –2 Підставляємо в рівняння 3х – 5у = 19: 3x + 10 = 19 3х = 9 x = 3 Відповідь: (3;–2) |
|
3) {3(2a – 1) + 6(7 – b) = 51 2(a + 6) – 7(1 + 6b) = 49 {6a – 3 + 42 – 6b = 51 2a + 12 – 7 – 42b = 49 {6a – 6b = 12 2a – 42b = 44 {a – b = 2 a – 21b = 22 {a = b + 2 b + 2 – 21b = 22 Розв'язуємо рівняння: b + 2 – 21b = 22 –20b = 20 b = –1 Підставляємо в рівняння а = b + 2: а = –1 + 2 = 1 Відповідь: (1;–1) |
4) {(3x – 2y)/4 – (4x + 5)/3 = –5 |•12 (6x – 5y)/2 + (2x + y)/5 = 9 |•10 {3(3x – 2y) – 4(4x + 5) = –60 5(6x – 5y) + 2(2x + y) = 90 {9x – 6y – 16x – 20 = –60 30x – 25y + 4x + 2y = 90 {–7x – 6y = –40 |•(–23) 34x – 23y = 90 |•6 {161x + 138y = 920 204x – 138y = 540 365x = 1460 x = 4 Підставляємо в рівняннz –7x – 6y = – 40: –28 – 6y = –40 –6у = –12 y = 2 Відповідь: (4;2) |
Завдання 1339
При якому значенні а сума x + у набуває найменшого значення, якщо:
{2x + 3у = 2a² – 12a + 8 |•2
3x – 2у = 3a² + 8a + 12 |•3
{4x + 6y = 4a² – 24a + 16
9x – 6y = 9a² + 24a + 36
13x = 13a² + 52 |:13
x = a² + 4
Підставляємо в рівняння 2х + 3у = 2а² – 12а + 8:
2(a² + 4) + 3y = 2a² – 12a + 8
3y = 2a² – 12a + 8 – 2a² – 8
3y = –12a
y = –4a
Сума x + y = a² + 4 + (– 4a) = a² + 4 – 4a = (a – 2)² і набуває найменшого значення при a = 2
Завдання 1340
При якому значенні а різниця x – у набуває найменшого значення, якщо:
{x – 5у = a² +10a + 1
4x + у = 4a² – 2a + 4 |•5
{x – 5y = a² + 10a + 1
20x + 5y = 20a² – 10a + 20
21x = 21a² + 21 |:21
x = a² + 1
Підставляємо в рівняння 4x + у = 4a² – 2a + 4:
4(a² + 1) + y = 4a² – 2a + 4
4a² + 4 + y = 4a² – 2a + 4
y = 4a² – 2a + 4 – 4a² – 4
y = –2a
Різниця x – y = a² + 1 + 2a = (a + 1)² і набуває найменшого значення при a = –1
Завдання 1341
Учні та учениці 7 класу зібралися на екскурсію. Якщо кожен з них здасть на екскурсію 12 грн 50 к., то для її оплати не вистачить 100 грн; якщо кожний внесе 16 грн, то утвориться надлишок у розмірі 12 грн. Скільки учнів та учениць у цьому класі?
Розв'язання
Нехай у класі х учнів, а екскурсія коштує у грн. Складаємо систему рівнянь:
{12,5x = y – 100 |•(–1)
16x = y + 12
{–12,5x = –y + 100
16x = y + 12
35x = 112
x = 32
Відповідь: 32 учні.
Завдання 1342
По колу, довжина якого дорівнює 100 м, рухаються два тіла. Коли вони рухаються в одному напрямі, то зустрічаються кожні 20 с. Коли вони рухаються в протилежних напрямах, то зустрічаються кожні 4 с. З якою швидкістю рухаються тіла?
Розв'язання
Нехай швидкість першого тіла дорівнює х м/с, а швидкість другого — у м/с. Складаємо систему рівнянь:
{20x – 20y = 100
4x + 4y = 100
{x – y = 5
x + y = 25
2x = 30
x = 15
Підставляємо в рівняння х – у = 5:
15 – y = 5
y = 10
Відповідь: 15 м/с, 10 м/с
Завдання 1343
Сплавили два злитки. Маса одного з них становила 105 г, і він містив 40% міді. Маса другого злитка становила 75 г. Знайдіть відсотковий вміст міді в другому злитку, якщо отриманий сплав містить 50% міді.
Розв'язання
1 спосіб
Нехай відсотковий вміст міді в другому сплаві х%, тоді маса міді в ньому 75х г. Складаємо рівняння:
105 • 0,4 + 75х = (105 + 75) • 0,5
42 + 75х = 180 • 0,5
75х = 90 – 42
75х = 48
х = 0,64
2 спосіб
1) 105 + 75 =180 (г) — маса двох злитків;
2) 180 • 0,5 = 90 (г) — маса міді в усьому сплаві;
3) 105 • 0,4 = 42 (г) — маса міді в першому злитку;
4) 90 – 42 = 48 (г) — маса міді в другому злитку;
5) 48 : 75 = 0,64 = 64% — відсотковий вміст міді в другому злитку.
Відповідь: 0,64 або 64%.
Завдання 1344
Скільки грамів 4%–го та скільки грамів 10%–го розчинів солі треба взяти, щоб одержати 180 г 6%–го розчину?
Розв'язання
Нехай треба взяти першого розчину х г, а другого розчину – у г.
|
Розчини |
Уміст солі |
Маса розчину, кг |
Маса солі в розчині, кг |
|
I |
4% |
х |
0,4х |
|
II |
10% |
у |
0,1у |
|
III |
6% |
180 |
0,06 • 180 |
Складаємо систему рівнянь:
{x + y = 180
0,04x + 0,1y = 0,06 • 180 |•(–10)
{x + y = 180
–0,4x – y = –108
0,6x = 72
x = 120
Підставляємо в рівняння х + у = 180:
120 + y = 180
y = 60
Відповідь: 120 г і 60 г.
Завдання 1345
У першому бідоні було молоко жирністю 3 %, а в другому — вершки жирністю 18 %. Скільки літрів молока та скільки літрів вершків треба взяти, щоб одержати 10 л молока жирністю 6 %?
Розв'язання
Нехай молока в першому бідоні було х г, а в другому – у г.
|
Бідони |
Уміст солі |
Маса розчину, кг |
Маса солі в розчині, кг |
|
I |
3% |
х |
0,03х |
|
II |
18% |
у |
0,18у |
|
III |
6% |
180 |
0,06 • 10 |
Складаємо систему рівнянь:
{x + y = 10
0,03x + 0,18y = 0,06 • 10
{x + y = 10
0,03x + 0,18y = 0,6
{x = 10 – у
0,03(10 – у) + 0,18y = 0,6
Розв'язуємо рівняння:
0,03(10 – у) + 0,18y = 0,6
0,3 – 0,03у + 0,18y = 0,6
0,3 – 0,15у = 0,6
0,15у = 0,3
у = 2
Підставляємо в рівняння х = 10 – у:
х = 10 – 2 = 8
Відповідь: 8 л і 2 л.
Завдання 1346
З одного поля зібрали по 40 ц ячменю з гектара, а з другого — по 35 ц з гектара. Усього було зібрано 2600 ц. Наступного року врожайність першого поля збільшилася на 10%, другого — на 20%. У результаті з двох полів разом було зібрано ячменю на 400 ц більше, ніж попереднього року. Знайдіть площу кожного поля.
Розв'язання
Нехай площа першого поля х га, а площа другого — у га, тоді з першого поля зібрали 40х ц ячменю, а з другого — 35у ц. Наступного року з першого поля зібрали на 0,1 • 40х = 4х ц ячменю більше, а з другого — на 0,2 • 35у = 7у ц. Складаємо рівняння:
{40x + 35y = 2600 |:(–5)
4x + 7y = 400
{–8x – 7y = –520
4x + 7y = 400
–4x = –120
x =30
Підставляємо в рівняння 4х + 7у = 400:
120 + 7y = 400
7y = 280
y = 40
Відповідь: 30 га, 40 га.
Завдання 1347
З одного поля зібрали по 45 ц пшениці з гектара, а з другого — по 40 ц з гектара. Усього було зібрано 1900 ц. Наступного року внаслідок посухи врожайність першого поля зменшилася на 20%, другого — на 15%. У результаті з двох полів разом було зібрано пшениці на 330 ц менше, ніж попереднього року. Знайдіть площу кожного поля.
Розв'язання
Нехай площа першого поля х га, а площа другого — у га, тоді з першого поля зібрали 45х ц пшениці, а з другого — 40у ц. Наступного року з першого поля зібрали на 0,2 • 45х = 9х ц пшениці менше, а з другого — на 0,15 • 40у = 6у ц менше. Складаємо рівняння:
{45x + 40y = 1900 |:(–5)
9x + 6y = 330
{–9x – 8y = –380
9x + 6y = 330
–2y = –50
y = 25
Підставляємо в рівняння 9х + 6у = 330:
9x + 150 = 330
9x = 180
x = 20
Відповідь: 20 га, 25 га.
Завдання 1348
Половину цукерок розфасували в мішечки по 500 г у кожний, а другу половину — у менші мішечки по 300 г у кожний. Усього вийшло 32 мішечки. Якою є маса всіх цукерок?
Розв'язання
Нехай було х мішечків по 500 г у кожному і у мішечків по 300 г у кожному, тоді маса мішечків з цукерками 500х г і 300у г. Складаємо рівняння:
{x + y = 32
500x = 300y
{x = 32 – у
500(32 – у) = 300y
Розв'язуємо рівняня:
500(32 – у) = 300y
16000 – 500у = 300у
800у = 16000
у = 20
Підставляємо в рівняння х = 32 – у:
х = 32 – 20 = 12
12 • 500 + 20 • 300 = 6 000 + 6 000 = 12 000 (г) = 12 (кг) – маса всіх цукерок
Відповідь: 12 кг.
Завдання 1349
Сума цифр двоцифрового числа дорівнює 11. Якщо до цього числа додати 63, то отримаємо число, записане тими самими цифрами у зворотному порядку. Знайдіть дане число.
Розв'язання
Нехай перша цифра х, друга цифра у, тоді шукане двоцифрове число ху = 10х + у, а записане тими самими цифрами у зворотному порядку ух = 10у + х. Складаємо систему рівнянь:
{х + у = 11
10х + у + 63 = 10у + х
{x = 11 – у
10(11 – у) + у + 63 = 10у + 11 – у
Розв'язуємо рівняння:
10(11 – у) + у + 63 = 10у + 11 – у
110 – 10у + у + 63 = 10у + 11 – у
–10у + у – 10у + у = 11 – 110 – 63
–18у = –162
у = 9
Підставляємо в рівняння х = 11 – у:
х = 11 – 9 = 2
Відповідь: 29
Завдання 1350
До деякого двоцифрового числа ліворуч і праворуч дописали цифру 1. У результаті отримали число, яке у 21 раз більше за дане. Знайдіть дане двоцифрове число.
Розв'язання
Нехай перша цифра х, друга цифра у, тоді шукане двоцифрове число ху = 10х + у, а записане згідно умови задачі число 1ху1 = 1000 + 10ху + 1. Складаємо рівняння:
1ху1 = 21ху
Запишемо так:
1000 + 10xу + 1 = 21ху
21ху – 10ху = 1000 + 1
11 • ху = 1001
ху = 91
Відповідь: 91.
Завдання 1351
Сума двох чисел дорівнює 28, а різниця їхніх квадратів становить 112. Знайдіть ці числа.
Розв'язання
Нехай більше число дорівнює х, а менше — у. Складаємо систему рівнянь:
{x + y = 28
x² – y² = 112
{x + y = 28
(x – y)(x + y) = 112
{x + y = 28
28(x – y) = 112
{x + y = 28
x – y = 4
2x = 32
x = 16
Підставляємо в рівняння х + у = 28:
16 + y = 28
y = 12
Відповідь: 16 і 12
Завдання 1352 Розгадайте кросворд
По горизонталі: 5. Пропорційність; 6. Куб; 9. Визначення; 14. Функція; 15. Тотожність; 18. Многочлен; 20. Коефіцієнт; 21. Декарт; 23. Означення; 24. Хорезмі
По вертикалі: 1. Корінь; 2. Аргумент; 3. Групування; 4. Степінь; 7. Квадрат; 8. Пряма; 10. Графік; 11. Абсциса; 12. Ординат; 13. Основа; 16. Одночлен;
17. Алгоритм; 19. Показник; 22. Точка.