Завдання 1199
Знайдіть два числа, якщо їхня сума дорівнює 63, а різниця дорівнює 19.
Розв'язання
Нехай шуканими числами є х і у. Складаємо систему рівнянь:
{х + у = 63
х – у = 19
2х = 82
х = 41
Підставимо знайдене значення змінної x у рівняння х + у = 63:
41 + у = 63
у = 22
Відповідь: 41 і 22.
Завдання 1200
Група із 46 туристів і туристок вирушила в похід на 10 човнах, частина з яких була чотиримісними, решта — шестимісними. Скільки було човнів кожного виду?
Розв'язання
Нехай було чотиримісних х човнів, а шестимісних – у човнів, тоді в чотиримісних човнах було 4х місць, а в шестимісних – 6у місць. Складаємо систему рівнянь:
{х + у = 10 |•(–4)
4х + 6у = 46
{–4х – 4у = –40
4х + 6у = 46
2у = 6
у = 3
Підставимо знайдене значення змінної у в рівняння х + у = 10:
х + 3 = 10
х = 7
Відповідь: було 7 чотиримісних і 3 шестимісних човнів.
Завдання 1201
Знайдіть два числа, якщо їхня різниця дорівнює 23, а сума подвоєного більшого із цих чисел і другого числа дорівнює 22.
Розв'язання
Нехай більше число х, а менше у, тоді подвоєне більше число 2х. Складаємо систему рівнянь:
{х – у = 23
2х + у = 22
3х = 45
х = 15
Підставимо знайдене значення змінної x у рівняння х – у = 23:
15 – у = 23
у = –8
Відповідь: 15 і –8.
Завдання 1202
Для того щоб нагодувати 4 коней і 12 корів, потрібно 120 кг сіна на день, а щоб нагодувати 3 коней і 20 корів — 167 кг сіна. Знайдіть денну норму сіна для коня та для корови.
Розв'язання
Нехай денна норма сіна для коня х кг, а для корови – у кг. Складаємо систему рівнянь:
{4х + 12у = 120 |•(–3)
3х + 20у = 167 |•4
{–12х –36у = –360
12х + 80у = 668
44у = 308
у = 7
Підставимо знайдене значення змінної у в рівняння 4х + 12у = 120:
4х + 12 • 7 = 120
4х + 84 = 120
4х = 120 – 84
4х = 36
х = 9
Відповідь: для коня денна норма сіна 7 кг і для корови — 9 кг.
Завдання 1203
За перший день 2 гусеничних трактори й один колісний зорали 22 га, а за другий день 3 гусеничних і 8 колісних — 72 га. Знайдіть, скільки гектарів землі може зорювати щодня один гусеничний трактор і скільки — один колісний.
Розв'язання
Нехай гусеничний трактор може зорати за день х га, а колісний – у га. Складаємо систему рівнянь:
{2х + у = 22 |•(–8)
3х + 8у = 72
{–16х – 8у = –176
3х + 8у = 22
–13х = –104
х = 8
Підставимо знайдене значення змінної x у рівняння 2х + у = 22:
2 • 8 + у = 22
16 + у = 22
у = 6
Відповідь: щодня гусеничний трактор може зорювати 8 га і колісний — 6 га.
Завдання 1204
Двоє робітників виготовили 135 деталей. Перший робітник працював 7 днів, а другий — 12 днів. Скільки деталей виготовляв щодня кожний робітник, якщо перший за 3 дні зробив на 3 деталі більше, ніж другий — за 4 дні?
Розв'язання
Нехай за день перший робітник виготовив х деталей, тоді другий робітник – у деталеу. Складаємо систему рівнянь:
{7х + 12у = 135
3х – 4у = 3 |•3
{7х + 12у = 135
9х – 12у = 9
16х = 144
х = 9
Підставимо знайдене значення змінної x у рівняння 3х – 4у = 3:
3 • 9 – 4у = 3
27 – 4у = 3
–4у = 3 – 27
–4у = –24
у = 6
Відповідь: щодня перший робітник виготовляв 9 деталей і другий робітник — 6 деталей.
Завдання 1205
Дві бригади працювали на збиранні яблук. Першого дня одна бригада працювала 5 год, а друга — 4 год, причому разом вони зібрали 40 ц яблук. Наступного дня бригади працювали з тією самою продуктивністю праці, при цьому перша бригада зібрала за 3 год на 2 ц більше, ніж друга — за 2 год. Скільки центнерів яблук збирала кожна бригада за 1 год?
Розв'язання
Нехай яблук за годину перша бригада збирала х ц, а друга бригада – у ц. Складаємо систему рівнянь:
{5х + 4у = 40
3х – 2у = 2 |•2
{5х + 4у = 40
6х – 4у = 4
11х = 44
х = 4
Підставимо знайдене значення змінної x у рівняння 3х – 2у = 2:
3 • 4 – 2у = 2
12 – 2у = 2
–2у = 2 – 12
–2у = –10
у = 5
Відповідь: яблук за 1 год перша бригада збирала 4 ц і друга — 5 ц.
Завдання 1206
За 6 однакових наборів олівців і 5 однакових циркулів заплатили 510 грн. Скільки коштує набір олівців і скільки — циркуль, якщо 3 набори олівців дорожчі за 1 циркуль на 150 грн?
Розв'язання
Нехай набір олівців коштує х грн, а набір циркулів – у грн. Складаємо систему рівнянь:
{6х + 5у = 510
3х – у = 150 |•(–2)
{6х + 5у = 510
–6х + 2у = –300
7у = 210
у = 30
Підставимо знайдене значення змінної у в рівняння 3х – у = 150:
3х – 30 = 150
3х = 150 + 30
3х = 180
х = 60
Відповідь: набір олівців коштує 60 грн і циркуль коштує 30 грн.
Завдання 1207
За 11 однакових зошитів і 8 однакових ручок заплатили 245 грн. Скільки коштує 1 зошит і скільки — 1 ручка, якщо 5 зошитів дорожчі за 4 ручки на 35 грн?
Розв'язання
Нехай зошит коштує х грн, а ручка – у грн. Складаємо систему рівнянь:
{11х + 8у = 245
5х – 4у = 35 |•2
{11х + 8у = 245
10х – 8у = 70
21х = 315
х = 15
Підставимо знайдене значення змінної x у рівняння 5х – 4у = 35:
5 • 15 – 4у = 35
75 – 4у = 35
–4у = 35 – 75
–4у = –40
у = 10
Відповідь: один зошит коштує 15 грн і одна ручка коштує 10 грн.
Завдання 1208
Із Києва й Вінниці, відстань між якими 256 км, виїхали одночасно назустріч один одному автобус і автомобіль, які зустрілися через 2 год після початку руху. Знайдіть швидкість кожного з них, якщо автобус за 2 год проїжджає на 46 км більше, ніж автомобіль за 1 год.
Розв'язання
Нехай швидкість автобуса х км/год, а автомобіля – у км/год. Складаємо систему рівнянь:
{2х + 2у = 256 |:2
2х – у = 46
{х + у = 128
2х – у = 46
3х = 174
х = 58
Підставимо знайдене значення змінної x у рівняння х + у = 128:
58 + у = 128
у = 70
Відповідь: швидкість автобуса 58 км/год і швидкість автомобіля 70 км/год.
Завдання 1209
Із двох станцій, відстань між якими 300 км, одночасно назустріч один одному вирушили пасажирський і товарний поїзди, які зустрілися через 3 год після початку руху. Якби пасажирський поїзд вирушив на 1 год раніше від товарного, то вони зустрілися б через 2,4 год після виходу товарного поїзда. Знайдіть швидкість кожного поїзда.
Розв'язання
Нехай швидкість пасажирського поїзда х км/год, а товарного – у км/год. Складаємо систему рівнянь:
{3х + 3у = 300 |:2
3,4х + 2,4у = 300 |:2
{х + у = 100 |•(–1,2)
1,7х + 1,2у = 150
{–1,2х + –1,2у = –120
1,7х + 1,2у = 150
0,5х = 30
х = 60
Підставимо знайдене значення змінної x у рівняння х + у = 100:
60 + у = 100
у = 40
Відповідь: пасажирський поїзд рухається зі швидкістю 60 км/год і товарний — 40 км/год.
Завдання 1210
Із села до станції вийшла пішохідка. Через 30 хв із цього села до станції виїхав велосипедист, який наздогнав пішохідку через 10 хв після виїзду. Знайдіть швидкість кожного з них, якщо за 3 год пішохідка проходить на 4 км більше, ніж велосипедист проїжджає за півгодини.
Розв'язання
10 хв = 10/60 год = 1/6 год; 30 хв = 30/60 год = 1/2 год
Нехай швидкість пішохода х км/год, а велосипедиста – у км/год
|
|
Швидкість (км/год) |
Час (год) |
Відстань (км) |
|
Пішохідка |
х |
(1/2 + 1/6) і 3 |
(1/2 + 1/6)х і 3х |
|
Велосипедист |
у |
1/6 і 1/2 |
1/6у і 1/2у |
Складаємо систему рівнянь:
{(1/2 + 1/6)х = 1/6 у
3х – 1/2у = 4
{1/2 х + 1/6 х = 1/6 у |•6
3х – 1/2у = 4
{3х + х = у
3х – 1/2у = 4
{у = 4х
3х – 1/2у = 4
Підставимо знайдене значення змінної у = 4х в рівняння 3х – 1/2 у = 4:
3х – 1/2• 4х = 4
3х – 2х = 4
х = 4
Підставимо знайдене значення змінної х в рівняння у = 4х:
у = 4 • 4
у = 16
Відповідь: швидкість пішохідки 4 км/год і швидкість велосипедиста 16 км/год.
Завдання 1211
Із Житомира до Одеси, відстань між якими 536 км, виїхав перший автомобіль. Через 2,5 год після початку руху першого автомобіля назустріч йому з Одеси виїхав другий автомобіль, який зустрівся з першим через 2 год після свого виїзду. Знайдіть швидкість кожного автомобіля, якщо перший за 2 год проїжджає на 69 км менше, ніж другий за 3 год.
Розв'язання
Нехай перший автомобіль їхав зі швидкістю х км/год, а другий автомобіль – у км/год.
|
Автомобілі |
Швидкість (км/год) |
Час (год) |
Відстань (км) |
|
I |
х |
(2,5 + 2) і 3 |
(2,5 + 2)х і 3х |
|
II |
у |
2 |
2у |
Складаємо систему рівнянь:
{(2,5 + 2)х + 2у = 536
2х + 69 = 3у
{4,5х + 2у = 536 |•6
2х – 3у = –69 |•2
{13,5х + 6у = 1608
4х – 6у = –138
17,5х = 1470
х = 84
Підставимо знайдене значення змінної х в рівняння 2х – 3у = –69:
2 • 84 – 3у = –69
168 – 3у = –69
–3у = –69 – 168
–3у = –237
у = 79
Відповідь: з Житомира перший автомобіль їхав зі швидкістю 84 км/год і з Одеси другий автомобіль — 79 км/год.
Завдання 1212
У двох бідонах було молоко. Якщо з першого бідона перелити в другий 10 л молока, то в обох бідонах молока стане порівну. Якщо з другого бідона перелити в перший 20 л молока, то в першому стане у 2,5 раза більше молока, ніж у другому. Скільки літрів молока було в кожному бідоні?
Розв'язання
Нехай молока в першому бідоні було х л, а в другому – у л. Складаємо систему рівнянь:
{х – 10 = у + 10
х + 20 = 2,5(у – 20)
{х – у = 20
х + 20 = 2,5у – 50
{х – у = 20
х – 2,5у = –70 |•(–1)
{х – у = 20
–х + 2,5у = 70
1,5у = 90
у = 60
Підставимо знайдене значення змінної у в рівняння х – у = 20:
х – 60 = 20
х = 80
Відповідь: молока в першому бідоні було 80 л і в другому — 60 л.
Завлання 1213
Коли до першого вагона електропотяга ввійшли 4 людини, а з другого вагона вийшли 4 людини, то в обох вагонах людей стало порівну. Якби до першого вагона ввійшли 2 людини, а до другого — 24 людини, то в першому вагоні стало б у 2 рази менше людей, ніж у другому. Скільки людей було спочатку в кожному вагоні?
Розв'язання
Нехай в першому вагоні – х пасажирів, а в другому – у пасажирів. Складаємо систему рівнянь:
{х + 4 = у – 4
(х + 2) • 2 = у + 24
{х – у = –8
2х + 4 = у + 24
{х – у = –8 |•(–1)
2х – у = 20
{–х + у = 8
2х – у = 20
х = 28
Підставимо знайдене значення змінної х в рівняння х – у = –8:
28 – у = –8
у = 36
Відповідь: спочатку в першому вагоні було 28 пасажирів і в другому — 36 пасажирів.
Завдання 1214
Моторний човен за 3 год руху проти течії річки та 2,5 год за течією проходить 98 км. Знайдіть власну швидкість човна та швидкість течії, якщо за 5 год руху за течією він проходить на 36 км більше, ніж за 4 год проти течії річки.
Розв'язання
Нехай власна швидкість човна х км/год, а швидкість течії у км/год.
|
|
Швидкість, км/год |
Час, год |
Відстань, км |
|
За течією |
х + у |
2,5 і 5 |
2,5(х + у) і 5(х + у) |
|
Проти течії |
х – у |
3 і 4 |
3(х – у) і 4(х – у) |
Складаємо систему рівнянь:
{3(х – у) + 2,5(х + у) = 98
5(х + у) – 4(х – у) = 36
{3х – 3у + 2,5х + 2,5у = 98
5х + 5у – 4х + 4у = 36
{5,5х – 0,5у = 98 |•18
х + 9у = 36
{99х – 9у = 1764
х + 9у = 36
100х = 1800
х = 18
Підставимо знайдене значення змінної х в рівняння х + 9у = 36:
18 + 9у = 36
9у = 36 – 18
9у = 18
у = 2
Відповідь: власна швидкість човна 18 км/год і швидкість течії річки 2 км/год.
Завдання 1215
Катер за 5 год руху за течією річки проходить на 70 км більше, ніж за 3 год руху проти течії. Знайдіть швидкість катера в стоячій воді та швидкість течії, якщо за 9 год руху озером він проходить стільки ж кілометрів, скільки за 10 год руху проти течії річки.
Розв'язання
Нехай власна швидкість човна х км/год, а швидкість течії у км/год.
|
|
Швидкість, км/год |
Час, год |
Відстань, км |
|
Човна |
х |
9 |
9х |
|
За течією |
х + у |
5 |
5(х + у) |
|
Проти течії |
х – у |
3 і 10 |
3(х – у) і 10(х – у) |
Складаємо систему рівнянь:
{5(х + у) – 3(х – у) = 70
9х = 10(х – у)
{5х + 5у – 3х + 3у = 70
9х – 10х + 10у = 0
{2х + 8у = 70 |:2
–х + 10у = 0
{х + 4у = 35
–х + 10у = 0
14у = 35
у = 2,5
Підставимо знайдене значення змінної у в рівняння –х + 10у = 0:
–х + 10 • 2,5 = 0
–х + 25 = 0
х = 25
Відповідь: власна швидкість човна 25 км/год і швидкість течії річки 2,5 км/год.
Завдання 1216
Дві майстерні мали пошити 75 костюмів. Коли перша майстерня виконала 60 % замовлення, а друга — 50 %, то виявилося, що перша майстерня пошила на 12 костюмів більше, ніж друга. Скільки костюмів мала пошити кожна майстерня?
Розв'язання
Нехай перша майстерня мала пошити х костюмів, а друга – у костюмів, тоді 60% замовлення першої майстрині становить 0,6х костюмів, а 50% другої – 0,5у костюмів, Складаємо систему рівнянь:
{х + у = 75
0,6х – 0,5у = 12 |•2
{х + у = 75
1,2х – у = 24
2,2х = 99
х = 45
Підставимо знайдене значення змінної у в рівняння х + у = 75:
45 + у = 75
у = 30
Відповідь: перша майстерня мала пошити 45 костюмів і друга — 30 костюмів.
Завдання 1217
Михайло та Галина мали разом 300 грн. Коли Михайло витратив 1/3 своїх грошей на придбання довідника з математики, а Галина — 1/6 своїх грошей на придбання довідника з української мови, то виявилося, що Михайло витратив на 5 грн менше, ніж Галина. Скільки грошей було в кожного з них спочатку?
Розв'язання
Нехай у Михайла було х грн, а в Галини – у грн, тоді Михайло витратив 1/3 х грн, а Галина – 1/6 у грн Складаємо систему рівнянь:
{х + у = 300
1/6 у –1/3 х = 5 |•6
{х + у = 300
у – 2х = 30
{х + у = 300
2х – у = –30
3х = 270
х = 90
Підставимо знайдене значення змінної у в рівняння х + у = 300:
90 + у = 300
у = 210
Відповідь: спочатку в Михайла було 90 грн і в Галини — 210 грн.
Завдання 1218
Відомо, що 4 кг огірків і 3 кг помідорів коштували 340 грн. Після того як огірки подорожчали на 50 %, а помідори подешевшали на 20 %, за 2 кг огірків і 5 кг помідорів заплатили 360 грн. Знайдіть початкову ціну 1 кг огірків і 1 кг помідорів.
Розв'язання
Нехай початкова ціна огірків х грн, а помідорів у грн. Після 50% подорожчання огірки стали коштувати (х + 0,5х) =1,5х грн, а після 20% здешевшення помідори – (у–0,2у) = 0,8у грн. Складаємо систему рівнянь:
{4х + 3у = 340
2 • 1,5х + 5 • 0,8у = 360
{4х + 3у = 340 |•(–3)
3х + 4у = 360 |• 4
{–12х – 9у = –1020
12х + 16у = 1440
7у = 420
у = 60
Підставимо знайдене значення змінної у в рівняння 4х + 3у = 340:
4х + 3 • 60 = 340
4х + 180 = 340
4х = 340 – 180
4х = 160
х = 40
Відповідь: огірків початкова ціна 40 грн і помідорів — 60 грн.
Завдання 1219
Відомо, що 2 однакові банки фарби та 3 однакові банки оліфи коштували 290 грн. Після того як фарба подешевшала на 10 %, а оліфа подорожчала на 40 %, за 6 банок фарби та 5 банок оліфи заплатили 728 грн. Знайдіть початкову ціну однієї банки фарби та однієї банки оліфи.
Розв'язання
Нехай початкова ціна банки фарби х грн, а оліфи у грн. Після подешевшення на 10% фарба стала коштувати (х – 0,1х) = 0,9х грн, а після подорожчання на 40% оліфа стала коштувати (у + 0,4у) = 1,4у грн. Складаємо систему рівнянь:
{2х + 3у = 290
6 • 0,9х + 5 • 1,4у = 728
{2х + 3у = 290 |•(–7)
5,4х + 7у = 728 |• 3
{–14х – 21у = –2030
16,2х + 21у = 2184
2,2х = 154
х = 70
Підставимо знайдене значення змінної х у рівняння 2х + 3у = 290:
2 • 70 + 3у = 290
140 + 3у = 290
3у = 290 – 140
3у = 150
у = 50
Відповідь: банки фарби початкова ціна 70 грн і банки оліфи — 50 грн.
Завдання 1220
Вкладник поклав у банк 14 000 грн на два різних рахунки. За першим із них банк виплачує 4% річних, а за другим — 6 % річних. Через рік вкладник одержав 680 грн відсоткових грошей. Скільки гривень він поклав на кожний рахунок?
Розв'язання
Нехай вкладник на перший рахунок поклав х грн, а на другий – у грн. Виплата 4% за першим вкладом становить 0,04х грн, а 6% за другим вкладом – 0,06у грн. Складаємо систему рівнянь:
{х + у = 14000
0,04х + 0,06у = 680 |• 50
{х + у = 14000 |•(–2)
2х + 3у = 34000
{–2х – 2у = –28000
2х + 3у = 34000
у = 6000
Підставимо знайдене значення змінної у в рівняння х + у = 14000:
х + 6000 = 14000
х = 8000
Відповідь: вкладник на перший рахунок поклала 8000 грн і другий рахунок — 6000 грн.
Завдання 1221
Вкладниця поклала в банк 12 000 грн на два різних рахунки. За першим із них банк виплачує 5% річних, а за другим — 7% річних. Через рік вкладниця отримала за 5 %–м вкладом на 240 грн відсоткових грошей більше, ніж за другим. Скільки гривень вона поклала на кожний рахунок?
Розв'язання
Нехай вкладниця на перший рахунок поклала х грн, а на другий – у грн. Виплата 5% за першим вкладом становить 0,05х грн, а 7% за другим вкладом – 0,07у грн. Складаємо систему рівнянь:
{х + у = 12000
0,05х – 0,07у = 240 |•100
{х + у = 12000 |•(–5)
5х – 7у = 24000
{–5х – 5у = –60000
5х – 7у = 24000
–12у = –36000
у = 3000
Підставимо знайдене значення змінної у в рівняння х + у = 12000:
х + 3000 = 12000
х = 9000
Відповідь: вкладниця на перший рахунок поклала 9000 грн і на другий — 3000 грн.
Завдання 1222
Маємо два сплави міді й цинку. Перший сплав містить 9%, а другий — 30% цинку. Скільки кілограмів кожного сплаву треба взяти, щоб одержати 300 кг сплаву, який містить 23% цинку?
Розв'язання
Нехай треба взяти першого сплаву х кг, а другого сплаву – у кг.
|
Сплав |
Уміст цинку |
Маса сплаву, кг |
Маса цинку в споаві, кг |
|
I |
9% |
х |
0,09х |
|
II |
30% |
у |
0,3у |
|
III |
23% |
300 |
0,23 • 300 |
Складаємо систему рівнянь:
{х + у = 300
0,09х + 0,3у = 0,23 • 300
{х + у = 300 |•(–0,3)
0,09х + 0,3у = 69
{–0,3х – 0,3у = –90
0,09х + 0,3у = 69
–0,21х = –21
х = 100
Підставимо знайдене значення змінної у в рівняння х + у = 300:
100 + у = 300
у = 200
Відповідь: першого сплаву треба взяти 100 кг і другого сплаву — 200 кг.
Завдання 1223
Маємо два водно–сольових розчини. Перший розчин містить 25%, а другий — 40% солі. Скільки кілограмів кожного розчину треба взяти, щоб одержати 50 кг розчину, який містить 34% солі?
Розв'язання
Нехай треба взяти першого розчину х кг, а другого розчину – у кг.
|
Розчини |
Уміст солі |
Маса розчину, кг |
Маса солі в розчині, кг |
|
I |
25% |
х |
0,25х |
|
II |
40% |
у |
0,4у |
|
III |
34% |
50 |
0,34 • 50 |
Складаємо систему рівнянь:
{х + у = 50
0,25х + 0,4у = 0,34 • 50
{х + у = 50 |•(–0,4)
0,25х + 0,4у = 17
{–0,4х – 0,4у = –20
0,25х + 0,4у = 17
–0,15х = –3
х = 20
Підставимо знайдене значення змінної х у рівняння х + у = 50:
20 + у = 50
у = 30
Відповідь: першого розчину треба взяти 20 кг і другого розчину — 30 кг.
Завдання 1224
Сума цифр двоцифрового числа дорівнює 15. Якщо поміняти його цифри місцями, то отримаємо число, яке менше від даного на 9. Знайдіть дане число.
Розв'язання
Нехай перша цифра х, друга цифра у, тоді шукане двоцифрове число ху = 10х + у, а з поміняними місцями цифрами число ух = 10у + х. Складаємо систему рівнянь:
{х + у = 15
10х + у – (10у + х) = 9
{х + у = 15
9х – 9у = 9 |:9
{х + у = 15
х – у = 1
2х = 16
х = 8
Підставимо знайдене значення змінної х у рівняння х – у = 1:
8 – у = 1
у = 7
Відповідь: шукане двоцифрове число 87.
Завдання 1225
Периметр прямокутника дорівнює 28 см. Якщо дві протилежні його сторони збільшити на 6 см, а дві інші зменшити на 2 см, то його площа збільшиться на 24 см². Знайдіть сторони даного прямокутника.
Розв'язання
Нехай перша сторона прямокутника х см, а друга сторона – у см, тоді площа прямокутника ху см, а периметр 2(х + у) см. Збільшена на 6 см перша сторона дорівнює (х + 6) см, а зменшена на 2 см друга сторона – (у – 2) см. Складаємо систему рівнянь:
{2(х + у) = 28
(х + 6)(у – 2) – ху = 24
{2х + 2у = 28
ху – 2х + 6у – 12 – ху = 24
{2х + 2у = 28
–2х + 6у = 36
8у = 64
у = 8
Підставимо знайдене значення змінної у в рівняння 2(х + у) = 28:
2(х + 8) = 28
2х + 16 = 28
2х = 12
х = 6
Відповідь: сторони прямокутника 6 см і 8 см.
Завдання 1226
Якщо кожну сторону прямокутника збільшити на 3 см, то його площа збільшиться на 45 см². Якщо дві протилежні сторони збільшити на 4 см, а дві інші зменшити на 5 см, то його площа зменшиться на 17 см². Знайдіть сторони даного прямокутника.
Розв'язання
Нехай одна сторона прямокутника х см, а друга сторона – у см, тоді площа дорівнює ху см. Збільшена на 3 см кожна сторона дорівнює (х + 3) см і (у + 3) см. Збільшена на 4 см перша сторона дорівнює (х + 4) см. а зменшена на 5 см друга сторона – (у – 5)см. Складаємо систему рівнянь:
(х + 3)(у + 3) – ху = 45
ху – (х + 4)(у – 5) = 17
{ху + 3х + 3у + 9 – ху = 45
ху – ху + 5х – 4у + 20 = 17
{3х + 3у = 36 |:3
5х – 4у = –3
{х + у = 12
5х – 4у = –3
{4х + 4у = 48 |•4
5х – 4у = –3
9х = 45
х = 5
Підставимо знайдене значення змінної у в рівняння х + у = 12:
5 + у = 12
у = 7
Відповідь: сторони прямокутника 5 см і 7 см.
Завдання 1227
(Задача з грецького фольклору.)
Віслюк і мул ідуть поруч з вантажем на спині. Віслюк скаржиться на непосильну ношу, а мул відповідає: «Чого ти скаржишся? Адже якщо я візьму один твій мішок, то моя ноша стане вдвічі важчою за твою. А якщо ти візьмеш один мій мішок, то твоя поклажа зрівняється з моєю». Скажіть же, мудрі математики, скільки мішків ніс віслюк і скільки ніс мул?
Розв'язання
Нехай віслюк ніс х мішків, а мул – у мішків. Складаємо систему рівнянь:
{2(х – 1) = у + 1
х + 1 = у – 1
{2х – 2 = у + 1
х + 1 = у – 1
{2х – у = 3
–х + у = 2
х = 5
Підставимо знайдене значення змінної х у рівняння –х + у = 2:
–5 + у = 2
у = 7
Відповідь: віслюк ніс 5 мішків і мул ніс 7 мішків.
Завдання 1228
(Задача з індійського фольклору.) Один каже другому: «Дай мені 100 рупій, і я буду вдвічі багатший за тебе». Другий відповідає: «А якщо ти даси мені 10 рупій, то я стану в 6 разів багатший за тебе». Скільки грошей було в кожного?
Розв'язання
Нехай у першого було х рупій, а у другого – у рупій. Складаємо систему рівнянь:
{х + 100 = 2(у – 100)
6(х – 10) = у + 10
{х + 100 = 2у – 200
6х – 60 = у + 10
{х – 2у = –300
6х – у = 70 |•(–2)
{х – 2у = –300
–12х + 2у = –140
–11х = –440
х = 40
Підставимо знайдене значення змінної х у рівняння х – 2у = –300:
40 – 2у = –300
–2у = –300 – 40
–2у = –340
у = 170
Відповідь: у першого було 40 рупій і в другого було 170 рупій.
Завдання 1229
Син 6 років тому був у 4 рази молодший від батька, а через 12 років він буде молодшим від батька у 2 рази. Скільки років батькові та скільки — синові?
Розв'язання
Нехай батькові х років, а синові – у років. Шість років тому батьковіі було (х – 6) років, а синові – (у – 6) років. Через 12 років батькові буде (х + 12) років, а синові – (у + 12) років. Складаємо систему рівнянь:
{х – 6 = 4(у – 6)
х + 12 = 2(у + 12)
{х – 6 = 4у – 24
х + 12 = 2у + 24
{х – 4у = –18
х – 2у = 12 •(–1)
{х – 4у = –18
–х + 2у = –12
–2у = –30
у = 15
Підставимо знайдене значення змінної у в рівняння х – 2у = 12:
х – 2 • 15 = 12
х = 42
Відповідь: батькові 42 роки і синові 15 років.
Завдання 1230
Бабуся 6 років тому була в 9 разів старша за онуку, а 4 роки тому — у 7 разів старша. Скільки років бабусі та скільки — онуці?
Розв'язання
Нехай бабусі х років, а онуці – у років. Шість років тому бабусі було (х – 6) років, а онуці – (у – 6) років. Чотири років тому бабусі було (х – 4) років, а онуці – (у – 4) років.Складаємо систему рівнянь:
{х – 6 = 9(у – 6)
х – 4 = 7(у – 4)
{х – 6 = 9у – 54
х – 4 = 7у – 28
{х – 9у = –48
х – 7у = –24 •(–1)
{х – 9у = –48
–х + 7у = 24
–2у = –24
у = 12
Підставимо знайдене значення змінної у в рівняння х – 9у = –48:
х – 9 • 12 = –48
х – 108 = –48
х = 60
Відповідь: бабусі 60 років і онуці 12 років.
Завдання 1231
Із двох селищ, відстань між якими дорівнює 45 км, одночасно назустріч один одному вирушили велосипедистка й пішохід, які зустрілися через 3 год після початку руху. Якби велосипедистка виїхала на 1 год 15 хв раніше, ніж вийшов пішохід, то вони зустрілися б через 2 год після виходу пішохода. З якими швидкостями рухалися велосипедистка й пішохід?
Розв'язання
1 год 15 хв = 1 год + 15 хв = 1 год + 0,25 год = 1,25 год
Нехай швидкість велосипедистки х км/год, а пішохода – у км/год.
|
Швидкість, км/год |
Час, год |
Відстань, км |
|
|
Велосипедистка |
х |
3 і (1,25 + 2) |
3х і (1,25 + 2)х |
|
Пішохід |
у |
3 і 2 |
3у і 3у |
Складаємо систему рівнянь:
{3х + 3у = 45 |:3
(1,25 + 2)х + 2у = 45
{х + у = 15 |•(–2)
3,25х + 2у = 45
{–2х – 2у = –30
3,25х + 2у = 45
1,25х = 15
х = 12
Підставимо знайдене значення змінної х у рівняння х + у = 15:
12 + у = 15
у = 3
Відповідь: велосипедистка рухалася зі швидкістю 12 км/год і пішохід — 3 км/год.
Завдання 1232
З пунктів A і B, відстань між якими дорівнює 24 км, одночасно назустріч одна одній вирушили дві туристки. Через 2 год після початку руху вони ще не зустрілися, а відстань між ними становила 6 км. Ще через 2 год одній з них залишилося пройти до пункту B на 4 км менше, ніж другій — до пункту A. Знайдіть швидкість кожної туристки.
Розв'язання
Нехай перша туристка рухається зі швидкістю х км/год, а друга – у км/год.
|
Швидкість, км/год |
Час, год |
Відстань, км |
|
|
I |
х |
2 і (2 + 2) |
3х і (2 + 2)х |
|
II |
у |
2 і (2 + 2) |
2у і (2 + 2)у |
Складаємо систему рівнянь:
{2х + 2у + 6 = 24
(2 + 2)х – (2 + 2)у = 4
{2х + 2у + 6 = 24
4х – 4у = 4 |:2
{2х + 2у = 18
2х – 2у = 2
4х = 20
х = 5
Підставимо знайдене значення змінної х у рівняння 2х – 2у = 2:
2 • 5 – 2у = 2
10 – 2у = 2
2у = 8
у = 4
Відповідь: швидкість першої туристки 5 км/год, швидкість другої — 4 км/год.
Завдання 1233
Велосипедист проїхав з пункту A до пункту B за запланований час, рухаючись із певною швидкістю. Якби він збільшив швидкість на 3 км/год, то прибув би до пункту B на 1 год раніше, а якби він проїжджав за годину на 2 км менше, то прибув би на 1 год пізніше. Знайдіть швидкість велосипедиста.
Розв'язання
Нехай швидкість велосипедистки х км/год, а запланований час – у км/год, тоді вся відстань – ху км. Якби швидкість була (х + 3) км/год, то часу було б потрачено (у – 1) год. Якби швидкість була (х – 2) км/год, то часу було б потрачено (у + 1) год. Складаємо систему рівнянь:
{(х + 3)(у – 1) = ху
(х – 2)(у + 1) = ху
{ху – х + 3у – 3 = ху
ху + х – 2у – 2 = ху
{–х + 3у = 3
х – 2у = 2
у = 5
Підставимо знайдене значення змінної у в рівняння х – 2у = 2:
х – 2 • 5 = 2
х – 10 = 2
х = 12
Відповідь: швидкість велосипедиста 12 км/год.
Завдання 1234
Вантаж було перевезено певною кількістю автомобілів з однаковою вантажопідйомністю. Якби на кожному з них вантажу було на 1 т більше, то вантажівок треба було б на 3 менше, а якби вантажу було на 2 т більше, то вантажівок треба було б на 5 менше. Знайдіть масу вантажу, який перевезли.
Розв'язання
Нехай було х вантажівок вантажопідйомністю у т, тоді маса вантажу – ху т. Якби на кожній машині було вантажу (у + 1) т, то вантажівок би було (х – 3) машин. Якби на кожній машині було вантажу (у + 2) т, то вантажівок було би (х – 5) машин. Складаємо систему рівнянь:
{(х – 3)(у + 1) = ху
(х – 5)(у + 2) = ху
{ху + х – 3у – 3 = ху
ху + 2х – 5у – 10 = ху
{х – 3у = 3 |•(–2)
2х – 5у = 10
{–2х + 6у = –6
2х – 5у = 10
у = 4
Підставимо знайдене значення змінної х у рівняння х – 3у = 3:
х – 3 • 4 = 3
х – 12 = 3
х = 15
ху = 15 • 4 = 60 (кг) – маса вантажу, яку перевезли.
Відповідь: 60 кг.
Завдання 1235
Автобус і маршрутне таксі виїжджають щодня назустріч одне одному за розкладом о 8 год з міст Вишневе та Яблуневе й зустрічаються о 8 год 10 хв. Відстань між містами 18 км. Одного дня автобус виїхав за розкладом, а таксі — із запізненням — о 8 год 9 хв. Тому зустрілися вони того дня о 8 год 15 хв. Знайдіть швидкості автобуса та маршрутного таксі.
Розв'язання
Нехай автобус рухається зі швидкістю х км/год, а маршрутне таксі – у км/год.
|
Швидкість, км/год |
Час, год |
Відстань, км |
||
|
За розкладом |
Автобус |
х |
8 год 10 хв – 8 год = 10 хв = = 10/60 год = 1/6 год |
1/6 х |
|
Таксі |
у |
1/6 у |
||
|
Поза розкладом |
Автобус |
х |
8 год 15 хв – 8 год = 15 хв = = 15/60 год = 1/4 год |
1/4 х |
|
Таксі |
у |
8 год 15 хв – 8 год 9 хв = 6 хв = = 6/60 год = 1/10 год |
1/10 у |
Складаємо систему рівнянь:
{1/6 х + 1/6 у = 18 |•6
1/4 х + 1/10 у = 18 |•20
{х + у = 108 |•(–2)
5х + 2у = 360
{–2х – 2у = –108
5х + 2у = 360
3х = 252
х = 84
Підставимо знайдене значення змінної х у рівняння х + у = 108:
60 + у = 108
у = 48
Відповідь: швидкість автобуса 48 км/год і швидкість маршрутного таксі 60 км/год.
Завдання 1236
З міста Сонячне до села Веселе о 9 год 5 хв і 9 год 45 хв виїхали з однаковою швидкістю два автобуси. З Веселого до Сонячного о 9 год 30 хв виїхав велосипедист, який зустрівся з першим автобусом о 9 год 45 хв, а з другим — о 10 год 15 хв. Знайдіть швидкості автобусів і велосипедиста, якщо відстань між Сонячним і Веселим становить 36 км.
Розв'язання
Нехай кожен автобус рухається зі швидкістю х км/год, а велосипедист – у км/год.
|
Швидкість, км/год |
Час, год |
Відстань, км |
Загальна відстань, км |
||
|
Сонячне- Веселе |
Автобус I |
х |
9 год 45 хв – 9 год 5 хв = 40 хв = 40/60 год = 2/3 год |
2/3 х | 36 |
|
Велосипедист |
у |
9 год 45 хв – 9 год 30 хв = = 15 хв = 15/60 год = 1/4 год |
1/4 у |
||
|
Веселе- Сонячне |
Автобус II |
х |
10 год 15 хв – 9 год 45 хв = = 30 хв = 30/60 год = 1/2 год |
1/2 х | 36 |
|
Велосипедист |
у |
10 год 15 хв – 9 год 30 хв = = 45 хв = 45/60 год = 3/4 год |
3/4 у |
Складаємо систему рівнянь:
{2/3 х + 1/4 у = 36 |•12
1/2 х + 3/4 у = 36 |•(–4)
{8х + 3у = 432
–2х – 3у = –144
6х = 288
х = 48
Підставимо знайдене значення змінної х у рівняння –2х – 3у = –144:
–2 • 48 – 3у = –144
–96 – 3у = –144
–3у = –144 + 96
–3у = –48
у = 16
Відповідь: швидкість кожного автобуса автобуса 48 км/год і швидкість велосипедиста 16 км/год.
Завдання 1237
Сума цифр двоцифрового числа дорівнює 9, причому цифра в розряді десятків більша за цифру в розряді одиниць. При діленні даного числа на різницю його цифр отримують неповну частку 14 і остачу 2. Знайдіть дане число.
Розв'язання
Нехай перша цифра х, друга цифра у, а шукане двоцифрове число ху = 10х + у. Сума цифр х + у = 9, а отримане число ху = (х – у) • 14 + 2. Складаємо систему рівнянь:
{х + у = 9
10х + у = (х – у) • 14 + 2
{х + у = 9
10х + у = 14х – 14у + 2
{х + у = 9 |•4
–4х + 15у = 2
{4х + 4у = 36
–4х + 15у = 2
19у = 8
у = 2
Підставимо знайдене значення змінної у в рівняння х + у = 9:
х + 2 = 9
х = 7
Відповідь: шукане двоцифрове число 72.
Завдання 1238
Різниця цифр двоцифрового числа дорівнює 6, причому цифра в розряді десятків менша від цифри в розряді одиниць. Якщо ж поділити дане число на суму його цифр, то отримаємо неповну частку 3 й остачу 3. Знайдіть дане число.
Нехай перша цифра х, друга цифра у, а шукане двоцифрове число ху = 10х + у. Різниця цифр у – х = 6, а отримане число ху = (х + у) • 3 + 3. Складаємо систему рівнянь:
{у – х = 6
10х + у = (х + у) • 3 + 3
{у – х = 6
10х + у = 3х + 3у + 3
{у – х = 6 |•2
–2у + 7х = 3
{2у – 2х = 12
–2у + 7х = 3
5х = 15
х = 3
Підставимо знайдене значення змінної х у рівняння у – х = 6:
у – 3 = 6
у = 9
Відповідь: шукане двоцифрове число 39.
Завдання 1239
В одному баку було 12 л води, а в другому — 32 л. Якщо перший бак долити доверху водою з другого бака, то другий бак залишиться наповненим на половину свого об’єму. Якщо другий бак долити доверху водою з першого, то перший бак залишиться наповненим на шосту частину свого об’єму. Знайдіть об’єм кожного бака.
Розв'язання
Нехай об'єм першого бака х л, а другого – у л.
|
Об'єм бака, л |
Було води, л |
Долили води, л |
Наповнення бака, л |
|
|
I |
х |
12 |
х – 12 |
1/6 х |
|
II |
у |
32 |
у – 32 |
1/2 у |
Складаємо систему рівнянь:
{32 – (х – 12) = 1/2 у |•2
12 – (у – 32) = 1/6 х |•6
{64 – 2(х – 12) = у
72 – 6(у – 32) = х
{64 – 2х + 24 = у
72 – 6у + 192 = х
{88 – 2х = у
264 – 6у = х
{–2х – у = –88
–х – 6у = –264 |•(–2)
{–2х – у = –88
2х + 12у = 528
11у = 440
у = 40
Підставимо знайдене значення змінної у в рівняння 88 – 2х = у:
88 – 2х = 40
–2х = –48
х = 24
Відповідь: перший бак має об'єм 24 л і другий — 40 л.
Завдання 1240
У двох посудинах місткістю 40 л і 60 л була деяка кількість води. Якщо в меншу посудину долити доверху води з більшої, то в більшій залишиться 5/7 тієї кількості води, що була в ній спочатку. Якщо в більшу посудину долити доверху води з меншої, то в меншій залишиться 5/14 тієї кількості води, що була в ній спочатку. Скільки літрів води було в кожній посудині спочатку?
Розв'язання
Нехай спочатку в першій посудині було х л, а в другій – у л.
|
Місткість посудини, л |
Було води, л |
Долили води, л |
Стало води, л |
|
|
I |
40 |
х |
40 – х |
5/14 х |
|
II |
60 |
у |
60 – у |
5/7 у |
Складаємо систему рівнянь:
{х – (60 – у) = 5/14 х |•14
у – (40 – х) = 5/7 у |•7
{14х – 14(60 – у) = 5х
7у – 7(40 – х) = 5у
{14х – 840 + 14у = 5х
7у – 280 + 7х = 5у
{14х – 5х + 14у = 840
7х + 7у – 5у = 280
{9х + 14у = 840
7х + 2у = 280 |•(–7)
{9х + 14у = 840
–49х – 14у = –1960
–40х = –1120
х = 28
Підставимо знайдене значення змінної х у рівняння 7х + 2у = 280:
7 • 28 + 2у = 280
196 + 2у = 280
2у = 84
х = 42
Відповідь: води спочатку в першій посудині було 28 л і в другій — 42 л.
Завдання 1241
Чи існує двоцифрове число, яке задовольняє таким умовам: цифра в розряді десятків цього числа на 2 більша за цифру в розряді його одиниць, а різниця між цим числом і числом, записаним тими самими цифрами, але у зворотному порядку, дорівнює: 1) 20; 2) 18? Якщо таке число існує, знайдіть його.
Нехай перша цифра х, друга цифра у, а шукане двоцифрове число ху = 10х + у. Різниця цифр
х – у = 2, а зворотнє число ух = 10у + х. Складаємо систему рівнянь:
|
1) 20 |
2) 18 |
|
Складаємо систему рівнянь: {х – у = 2 10х + у – (10у + х) = 20 {х – у = 2 10х + у – 10у – х = 20 {х – у = 2 |•9 9х – 9у = 20 {9х – 9у = 18 9х – 9у = 20 Система не має розв'язків. Відповідь: такого числа не існує |
Складаємо систему рівнянь: {х – у = 2 10х + у – (10у + х) = 18 {х – у = 2 10х + у – 10у – х = 18 {х – у = 2 |•9 9х – 9у = 18 {9х – 9у = 18 9х – 9у = 18 Система має безліч розв'язків. Розв'язки задовільняють рівняння х = у + 2, тому (1;3),(2;4),(3;5),(4;6),(5;7),(6;9). Відповідь: 13, 24, 35, 46, 57, 69. |
Завдання 1242
У рівності 4(0,5x – 3) = 3x + * замініть зірочку виразом, щоб утворилося рівняння, яке:
|
1) не має коренів |
2) має безліч коренів |
3) має один корінь |
|
4(0,5x – 3) = 3x + * 2x – 12 = 3x + * 2x – 3х – 12 = * –х – 12 = * Якщо * = –х, маємо рівняння: –х – 12 = –х –х + х = 12 0х = 12 Не має коренів. |
4(0,5x – 3) = 3x + * 2x – 12 = 3x + * 2x – 3х – 12 = * –х – 12 = * Якщо * = –х – 12, маємо рівняння: –х – 12 = –х – 12 –х + х = –12 + 12 0х = 0 Безліч коренів. |
4(0,5x – 3) = 3x + * 2x – 12 = 3x + * 2x – 3х – 12 = * –х – 12 = * Якщо * = х, маємо рівняння: –х – 12 = х –х – х = 12 –2х = 12 х = –6 Один корінь. |
Завдання 1243
На рисунку 76 зображено графік руху туристки від залізничної станції до туристичного табору. Користуючись графіком, визначте:
1) туристка подолала відстань 18 км за 5 год;
2) через 4 год після початку руху туристка була на відстані 12 км;
3) після виходу зі станції туристка зробила першу зупинку через 1,5 год тривалістю 0,5 год;
4) від станції до першої зупинки туристка рухалася зі швидкістю: 6 км : 1,5 год = 4 км/год;
5) від першої зупинки до другої зупинки туристка рухалася зі швидкістю:
(9 км – 6 км) : 1 год = 3 км/год.
Завдання 1244 Графік функції
|
1) y = (2x – 1)(4x2 + 2x + 1) – 8x3 y = (2x – 1)((2x)2 + 2x • 1 + 12)–8x3 y = ((2x)3 – 13) – 8x3 y = 8x3 – 13 – 8x3 у = –13 у = –1 |
|
||||||||
|
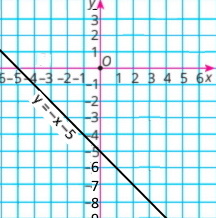
2) y = (x + 1)(x + 4) – (x + 3)² y = (x² + 4х + х + 4) – (x² + 6х + 3²) y = (x² + 5х + 4) – (x² + 6х + 3²) y = x² + 5х + 4 – x² – 6х – 9 y = –x – 5
|
 |
||||||||
|
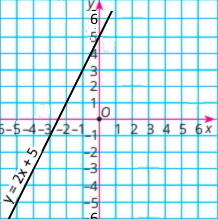
3) y = (0,5x + 2)² – (0,5x – 1) (0,5x + 1). y = ((0,5x)² + 2•0,5x•2 + 2²) – ((0,5x)² – 1²) y = (0,25x² + 2x + 4) – (0,25x² – 1) y = 0,25x² + 2x + 4 – 0,25x² + 1 y = 2x + 5
|
 |
||||||||
Завданння 1245
Побудуйте графік функції. Використовуючи побудований графік, визначте, при яких значеннях a пряма y = a має із цим графіком рівно дві спільні точки.
|
у = 2х + 7, якщо x < –2 |
у = –1,5х , якщо –2 ≤ x ≤ 2 |
у = х – 5, якщо x > 2 |
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
|
||||||||||||||||||||
Завдання 1246
Подайте вираз 12ab у вигляді різниці квадратів двох многочленів. Скільки розв’язків має задача?
Завдання 1247
Доведіть, що при будь–якому цілому значенні a значення виразу ділиться націло на 3.
(a – 3)(a² – a + 2) – a(a – 2)² + 2a = (a – 3)(a² – a + 2) – a(a² – 4a + 4) + 2a =
= a3 – a² + 2a – 3a² + 3a – 6 – a3 + 4a² – 4a + 2a = 3a – 6 = 3(a – 6).
Отриманий вираз ділиться націло на 3.
Завдання 1248 Тотожність
(a – bc)² – 2(b²c² – a²) + (bc + a)² = 4a².
(a – bc)² – 2(b²c² – a²) + (bc + a)² =
= (a² – 2abc + b²c²) – (2b²c² – 2a²) + (b²c² + 2abc + a²) =
= a² – 2abc + b²c² – 2b²c² + 2a² + b²c² + 2abc + a² = a² + 2a² + a² = 4a²
Завдання 1249 Розклад на множники
1) 4kn + 6ak + 6an + 9a² = (4kn + 6ak) + (6an + 9a²) = 2k(2n + 3a) + 3a(2n + 3a) =
= (2k + 3a)(2n + 3a)
2) b6 – 4b4 + 12b² – 9 = b6 – (4b4 – 12b² + 9) = (b3)2 – ((2b²)² – 2 • 2b² • 3 + 3²) =
= (b3)2 – (2b² – 3)² = (b3 – (2b² – 3))(b3 + (2b² – 3)) = (b3 – 2b² + 3)(b3 + 2b² – 3)
3) y4(x² + 8x + 16) – a8= y4(x² + 2 4x + 4²) – a8 = y4(x + 4)² – a8 = (y²(x + 4))² – (a4)²=
= (y²x + 4y² – a4)(y²x + 4y² + a4)
4) 9x² – 6x – 35 = 9x² – 6x + 1 – 36 = (9x² – 6x + 1) – 36 =
= ((3x)² – 2 • 3x • 1 + 1²) – 6² = (3x – 1)² – 6²= (3x – 1 – 6)(3x – 1 + 6)=(3x – 7)(3x + 5)
Завдання 1250
Відомо, що x + y = a, xy = b, x² + y² = c. Знайдіть залежність між a, b і c.
x² + y² = (x + y)² – 2xy, підставивши значення змінних, отримаємо c = a² – 2b
Завдання 1251
Точки A(2;3) і B(5;a) належать прямій y = kx. Знайдіть значення a.
A(2;3) належать прямій y = kx, тому 3 = 2k, k = 1,5.
B(5;a) належать прямій y = 1,5x, тому a = 1,5 • 5 = 7,5
Завдання 1252
Знайдіть такі значення x, при яких вираз (a – 1)² + 4(a – 1) – x можна було б розкласти на множники за формулою квадрата суми.
(a – 1)² + 4 (a – 1) – x = (a – 1)² + 2 • 2(a – 1) – x = (a – 1)² + 2 • (a – 1) • 2 – x
Вираз можна розкласти на множники за формулою квадрата суми, якщо замість х підставити –4, тобто х = –4
Отримаємо (a – 1)² + 2 • (a – 1) • 2 + 4 = (а – 1)² + 2²
Завдання 1253
Графіки функцій y = ax + 12 і y = (3 – a) x + a перетинаються в точці з абсцисою 2. Знайдіть ординату точки їхнього перетину.
{ах + 12 = y
(3 – а)х + а = у
Точка з координатами (2:у) належить рівнянням.
{2а + 12 = y
6 – 2а + а = у
{2а + 12 = y
–а + 6 = у |•2
{2а + 12 = y
–2а + 12 = 2у
3у = 24
у = 8
Відповідь: точка перетину (2;8).
Завдання 1254
Доведіть, що квадрат натурального числа має непарну кількість дільників.
Нехай n – натуральне число, а х – дільник числа n, тоді число у, де у = n : х також є дільником n. Якщо маємо n², то дільниками цього числа будуть n,x, n/x, тобто три дільники – непарна кількість.