
Завдання 357 Протилежні числа
|
а. –5
|
б. +3
|
в. –12
|
г. +15
|
д. –15
|
е. –15
|
Завдання 358
|
а. –х = 2, х = –2
в. х = –(–8), х = 8
д. х = –(+15), х = –15
|
б. –x = –3, х = 3
г. –х = +11, х = –11
е. –х = –(–19), х = –19
|
Завдання 359
Протилежні числа: –2, –4, –5, –7, –9, –10.
Завдання 360
а. |–45| + |–71| = 45 + 71 = 116
б. |9,7| + |–9,7| = 9,7 + 9,7 = 19,4
в. |–8,25| – |–5,03| = 8,25 – 5,03 = 3,22
г. |+12,5| – |7,5| = 12,5 – 7,5 = 5
д. |–(–15)| – |–(+8)| = 15 – 8 = 7
е. |1,05| + |0| = 1,05 + 0 = 1,05
Завдання 361
Два друга підіймалися на Говерлу. Знайдіть весь пройдений хлопцями шлях, якщо один із них піднявся на висоту 1052 м і повернувся назад, а другий піднявся лише на 597 м і повернувся назад. Під час обчислення вважати підйом угору додатнім напрямком, а спуск – від’ємним.
Розв'язання
1) |1052| + |–1052| = 1052 + 1052 = 2104 – пройшов перший друг;
2) |597| + |–597| = 597 + 597 = 1194 – пройшов другий друг;
3) 2104 + 1194 = 3298 – весь шлях.
Відповідь: 3298 км.
Завдання 362
а. 127 – 351 + (–65) = 127 – 351 – 65 = –289
б. –25 + 85 + (–35) – (–45) = –25 + 85 –35 + 45 = 70
в. 364 – 565 – 164 – 235 = –600
г. –36 + (–58) – (–46) – 0 + (+82) = –36 – 58 + 46 – 0 + 82 = 34
Завдання 363
а. –0,25 • (–36) • 4 = –0,25 • 4 • (–36) = –1 • (–36) = 36
б. 50 • (–23) • 0,2 = 50 • 0,2 • (–23) = 10 • (–23) = –230
в. 32 • (–1,25) = –40
г. 125 • (–12) • (–4) = 125 • (–4) • (–12) = –500 • (–12) = 6000
д. (–152) • 0,32 + 0,68 • (–152) = (–152) • (0,32 + 0,68) = (–152) • 1 = –152
Завдання 364
|
а. 15 : (–3) = –5
г. 60 : (–15) = –4
ж. 0 : (–5) = 0
|
б. –27 : (–9) = 3
д. –135 : 5 = –27
з. –55 : 10 = –5,5
|
в. 13 : (–1) = –13
е. 84 : (–21) = –4
і. –(–72) : (–6) = –12
|
Завдання 365
а. 42 : (–7) + 65 : (–7 – 6) = 42 : (–7) + 65 : (–13) = –6 + (–5) = –11
б. (–243 – 225 : (–17 + 32)) + 128 : (–32) – (–542) =
= (–243 – 225 : 15) + (–4) – (–542) = –243 – 15 + 538 = 280
в. 25 – 36 : (–4) + (–11) = 25 – (–9) + (–11) = 34 + (–11) = 23
г. (–10) – (–6) + (–9) : 3 = –10 – (–6) + (–3) = –10 + 6 + (–3) = –7
д. 3 • (3 – 5) • 4 + ((–18) + (–2)) : 2 • (–2) = 3 • (–2) • 4 + (–20) : 2 • (–2) =
= –24 + (–10) • (–2) = –24 + 20 = –4
е. –15 – (15 + (–9)) • 2 : (–3) = –15 – 6 • 2 : (–3) = –15 – 12 : (–3) = –15 – (–4) =
–15 + 4 = –11
Завдання 366
7,5; –1,2; 6; –5,5; +14; –3,75; 0; –1; 17 5/8 = 17,625; –8 2/5 = –8,04
У порядку зростання: –8 2/5; –5,5; –3,75; –1,2; –1; 0; 6; 7,5; +14; 17 5/8
|
Додатні дробові числа:
|
Від’ємні не дробові числа:
|
Від’ємні не цілі числа:
|
|
7,5; 17 5/8
|
–1
|
–1,2; –5,5; –3,75; –8 2/5
|
Завдання 367
–8 < х < 6, якщо цілі числа х = –7; –6; –5; –4; –3; –2; –1; 0; 1; 2; 3; 4; 5
Так, ці числа будуть раціональними.
Завдання 368
|
а. –56 < 3,5
г. –0,54 = –0,540
ж. –6 3/4 < –3 3/4
|
б. 5,2 > –5,2
д. –0,08 > –0,80
з. –3/5 > –5/6
|
в. –3,6 < – 3,06
е. 5 1/2 > –7 1/2
і. –1 3/7 > –7/3
|
Завдання 369
Четверо друзів живуть на одній вулиці. Їхні будинки розташовані на різній відстані від високого дерева, так як показано на фото.
Вулиця перетворилася на координатну пряму. Координати: A(–1,5); B(1,8); C(5,5); D(9,5).
|
а. 1,8 > –1,5
е. 1,8 > 0
|
б. 5,5 < 9,5
ж. 5,5 > 0
|
в. –1,5 < 9,5
з. –9,5 < 0
|
д. 5,5 > 1,8
i. –(–1,5) > 0
|
д. 1,8 < 9,5
к. –1,8 < 5,5
|
Завдання 370
Для приготування морозива яєчно-молочну суміш спочатку нагрівають до 60°С, а потім прогрівають до 82°С та знімають з вогню для охолодження. Коли температура цієї маси стає 15°С, до неї додаються охолоджені вершки. У результаті отримують морозиво температурою –2,5°С. Запишіть ланцюжок зміни температури суміші в процесі приготування.
|
Зміна температури:
|
60 + x = 82
х = 22
|
82 – х = 15
х = 67
|
15 – х = –2,5
х = 17,5
|
|
Ланцюжок зміни температури:
|
60 + 22 – 67 – 17,5 = –2,5 (°С)
|
||
Завдання 371
Під час темперування чорного шоколаду його нагрівають до 48°С, а потім охолоджують до 28°С і знову нагрівають до 32°С. Молочний шоколад нагрівають до 48°С, охолоджують до 27°С і знову нагрівають до 30°С. Знайдіть суму змін температур у процесі темперування окремо кожного виду шоколаду.
|
Чорний шоколад
|
Молочний шоколад
|
|
48 – 20 + 4 = 32 (°С)
або
48 – 28 + 32 = 52 (°С)
|
48 – 21 + 3 = 30 (°С)
або
48 – 27 + 30 = 51 (°С)
|
Завдання 372
|
а. –2,6 + 8,7 = 6,1
б. 6,3 – 48,3 = –42
в. –14,65 – 6,12 = –20,77
г. –23,05 + 23,5 = 0,45
д. –8,4 + 8,4 = 0
е. –45,2 + 0 = –45,2
|
ж. 0 – (–12,6) = 12,6
з. 36,52 + 56,23 = 92,75
і. –5 1/2 + 6 3/4 = –5,5 + 6,75 = 1,25
к. –9 5/12 – 14 7/24 = –9 10/24 – 14 7/24 = –23 17/24
л. –85 3/7 + 85 3/7 = 0
м. 2 1/5 – (–1 7/20) = 2 4/20 + 1 7/20) = 3 11/20
|
Завдання 373
а. –3/4 + (5,6) = –0,75 + 5,6 = 4,85
б. –0,25 + (–6 1/2) = –0,25 + (–6,5) = –6,75
в. –7 4/5 + (–0,23 + (–1,8)) = –7,8 + (–0,23 + (–1,8)) = –7,8 + (–2,03) = –9,83
г. (–5/8 + (–4 5/6)) + (–18 + (–0,5)) = (–5/8 + (–4 5/6)) + (–18,5) =
= (–15/24 + (–4 20/24)) + (–18 5/10) = (–4 35/24) + (–18 1/2) = (–4 35/24) + (–18 12/24) =
= (–22 47/24) = –23 23/24
д. (–13,47 – (–3 1/4)) – 9,78 = (–13,47 – (–3,25)) – 9,78 = –10,22 – 9,78 = –20
Завдання 374
|
а. –0,4 • 1,2 = –0,48
б. –2,5 • (–8) = 20
в. –1,5 • 0,3 = –0,45
г. –1,8 • 0 = 0
д. –0,5 • 1,6 = –0,8
е. –0,5 • (–0,12) = 0,06
|
ж. –1,4 • (–0,3) = 0,42
з. –1,25 • (–0,8) = 1
і. 0,3~2 = 0,3 • 0,3 = 0,09
к. (–0,1)~2 = (–0,1) • (–0,1) = 0,01
л. 0,2~3 = 0,2 • 0,2 • 0,2 = 0,008
м. (–0,5)3 = (–0,5) • (–0,5) • (–0,5) = –0,125
|
Завдання 375
а. –4,569 : (–0,3) = 15,23
б. –58,4 : 1,6 = –36,5
в. –34/55 : (– 17/66) = –34/55 • (– 66/17) = 12/5 = 2 2/5
г. –2 1/36 : 5 4/9 = –73/36 : 49/9 = –73/36 • 9/49 = –73/4 • 1/49 = –73/196
д. –2,8 : (–2/7) = –28/10 : (–2/7) = –28/10 • (–7/2) = 98/10 = 9,8
е. (–11/15 + 17/30) : (19/54 – 7/9) = (–22/30 + 17/30) : (19/54 – 42/54) =
= (–5/30) : (–23/54) = (–1/6) • (–54/23) = 9/23
Завдання 376
а. (–3 1/2) • 2,8 = (–3,5) • 2,8 = –9,8
б. (–1,6) • 1 3/4 = (–1,6) • 1,75 = –2,8
в. –0,6 • (–5 1/4) = –0,6 • (–5,25) = 3,15
г. 1,2 • (–0,12) = –0,144
д. –25,4 • (–0,8) = 20,32
е. 3,5 • (–0,2) • 12,6 = –8,82
ж. –0,25 • (–145,23) • (–0,4) = –14,523
з. -0,05 • (–45,67) • 20 = 45,67
і. 5,75 • (–145,36) • 4/23 = –835,82 • 4/23 = –83582/100 • 4/23 = –3634/25 = –145,36
к. –15 2/3 • 3/94 • (–4/5) = –47/3 • 3/94 • (–4/5) = –1/2 • (–4/5) = 2/5
Завдання 377
Подорожуючи, родина Петренків проїхала автомобілем 500 км. Марічка щогодини записувала показники температури повітря на вулиці, що показував бортовий комп’ютер авто. Знайдіть середню температуру повітря протягом усієї цієї подорожі.
Розв'язання
1) –7 + (–5) + (–4,5) + (–4) + (–2) + 0 + 1,5 = –22,5 + 1,5 = –21 – сума температур протягом подорожі;
2) –21 : 7 = –3 – середня температура повітря протягом подорожі.
Відповідь: –3°С.
Завдання 378
Маленька Іринка бавилась калькулятором старшої сестри, на якому світилося число –81. Іринка тричі поділила його на –3, потім поділила на 6, потім помножила на –10 і піднесла до куба результат. Яке зараз число світиться на екрані калькулятора?
Розв'язання
(–81 : (–3) : (–3) : (–3) : 6 • (–10))3 =
= (27 : (–3) : (–3) : 6 • (–10))3 = ((–9) : (–3) : 6 • (–10))3 =
= (3 : 6 • (–10))3 = (0,5 • (–10))3 = (–5)3 = (–5) • (–5) • (–5) = –125
Відповідь: на екрані світиться число –125.
Завдання 379 Ознаки подільності чисел
Друзі грали у настільну гру, ведуча записувала бали, що отримували гравці. У Павла були записані додатні числа, більші за 18, але менші за 46, що кратні 5, та від’ємні числа, менші за –23, але більші за –37, що кратні 3. У Михайла були записані додатні числа, більші за 15, але менші за 55, що кратні 10, та від’ємні числа, менші за –21, але більші за –37, що кратні 6. Поміркуй та скажи, хто з хлопців став переможцем у цій грі, якщо за умовами виграє той, хто отримав найбільшу суму балів?
Розв'язання
18 < x < 46, що кратні 5, х = 20; 25; 30; 35; 40; 45.
–37 < x < –23, що кратні 3, х = –24; –27; –30; –33; –36.
20 + 25 + 30 + 35 + 40 + 45 + (–24) + (–27) + (–30) + (–33) + (–36) = 195 + (–150) = 45 (б.) – сума Павла;
15 < x < 55, що кратні 10, х = 20; 30; 40; 50.
–37 < x < –21, що кратні 6, х = –24; –30; –36.
20 + 30 + 40 + 50 + (–24) + (–30) + (–36) = 140 + (–90) = 50 (б.) – сума Михайла.
Відповідь: переможцем став Михайло.
Завдання 380
а. 7 12/33 + 4 5/11 : (–7) – 8/105 : (–16/35) + (–2/3)3 : 4 8/9 = 6 5/6
б. (–34 : (–3 7/9) : (– 1 1/17 • 4 1/4 ) • (56,49 – (2,817/0,2)) = –84,81
Завдання 381
|
а. –0,12 : (–6) = 0,02
г. –9 : (–0,15) = 60
|
б. –3,6 : (–0,4) = 9
д. –1 : 0,5 = –2
|
в. 6 : (–0,12) = –50
е. 7,2 : (–0,09) = –80
|
Завдання 382
Лежать на осі абсцис: K, H
Лежать на осі ординат: M, F
Мають протилежні координати:
Мають рівні абсцису з ординатою: N, X
Рівні лише абсциси: B i L; C i G; M i F; E i X; D i N
Рівні лише ординати: D i A; E i B; K i H; X i L; N i G
Початок координат: O
Завдання 383
Точки з координатами (0;5), (3;4), (6;3), (0;–5), (–3;–4), (–6;–3).
Утворені три відрізки перетинаються в точці О.
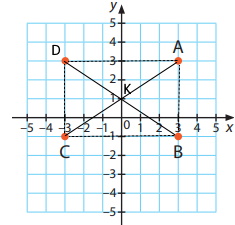
Завдання 384
А, В, С – вершини прямокутника АВСD. Виконуючи обчислення, вважайте, що одиничний відрізок дорівнює 1 см.
а. координати четвертої вершини D(–3;3)
б. координати точки перетину діагоналей прямокутника K(0;1)
в. периметр прямокутника; P = (6 + 4) • 2 = 20 (cм)
г. площу прямокутника. S = 6 • 4 = 24 (cм²)
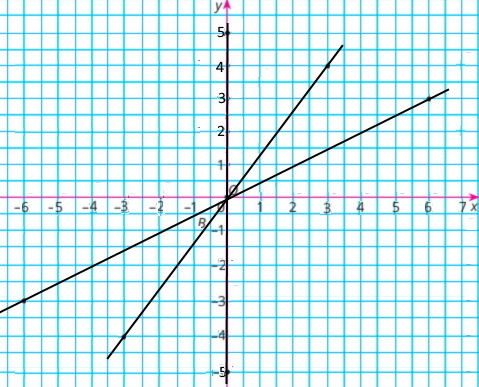
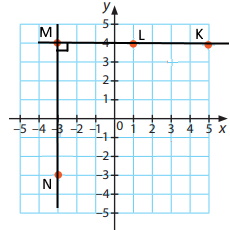
Завдання 385
На координатній площині позначте точки M(–3;4), N(–3;–3), L(1;4), K(5;4). Дайте відповіді на питання.
а. Координати точки перетину прямих MN і KL: M(–3;4)
б. Координати точки перетину прямої MN з віссю абсцис: (–3;0)
в. Координати точки перетину прямої KL з віссю ординат: (0;4)
г. Пряма MN з віссю Оу не перетинається.
д. Пряма KL з віссю ОХ не перетинається.
е. Градусна міра кута М дорівнює 90°
Завдання 386
Знайдіть кути трикутника АВС, якщо один з них дорівнює 70°, а два інші – рівні. Назвіть вид цього трикутника.
Розв'язання
(180° – 70°) : 2 = 55°
Відповідь: 70°; 55°; 55°; трикутник рівнобедрений.
Завдання 387
Знайдіть гострі кути прямокутного трикутника PRS (R = 90°), якщо кут, вертикальний P, дорівнює 30°.
Розв'язання
180° – (90° + 30°) = 60°
Відповідь: ∠P = 30°; ∠S = 60°.
Завдання 388
Знайдіть N трикутника KMN, якщо К = 50°, а кут суміжний з M, дорівнює 115°.
Розв'язання
1) 180° – 115° = 65° – ∠М;
2) 180° – (50° + 65°) = 65° – ∠N.
Відповідь: ∠N = 65°.
Завдання 389
Знайдіть градусну міру В трикутника АВС, якщо С = 65°, а промінь АК ділить А навпіл і утворює зі стороною АВ кут 42°.
Розв'язання
1) 42° + 42° = 84° – ∠A.
2) 180° – (84° + 65°) = 31° – ∠B.
Відповідь: ∠B = 31°.
Завдання 390
Знайдіть градусні міри кутів рівнобедреного трикутника, якщо кут при вершині на 20° більший за будь-який кут рівностороннього трикутника.
Розв'язання
1) 60° + 20° = 80° – кут при вершині.
2) (180° – 80°) : 2 = 50° – кут при основі.
Відповідь: 80°; 50°; 50°.
Завдання 391
Знайдіть градусні міри кутів трикутника ХYZ, Якщо X + Y = 130°, Y + Z = 110°.
Розв'язання
х + y + z = 180°
1) 180° – 130° = 50° – це кут Z;
2) 110° – 50° = 60° – це кут Y;
3) 130° – 160° = 70° – це кут X.
Відповідь: ∠X = 70°; ∠Y = 60°; ∠Z = 50°.