Завдання 822
Чи існують трикутники:
а) трикутник, сторони якого дорівнюють 11 см, 7 см і 8 см? Так
Чому? 7 + 8 > 11; 11 + 7 > 8; 11 + 8 > 7
б) чотирикутник, сторони якого дорівнюють 3 см, 3 см, 3 см і 10 см? Ні
Чому? 3 + 3 + 3 < 10
Завдання 823
Чи можуть кути трикутника дорівнювати:
а) 37°, 43° і 110° Ні, бо 37° + 43° + 110° > 180°
б) 37°, 43° і 100°? Так, бо 37° + 43° + 100° = 180°
Завдання 624
Міри двох кутів трикутника дорівнюють 25° і 40°. Яка міра третього кута? Б 115°
180° – (25° + 40°) = 115°
Завдання 825
Сума всіх кутів квадрата дорівнює 90° • 4 = 360°
Завдання 826
Чи можуть усі кути одного чотирикутника бути:
а) гострими; Ні
б) прямими; Так (прямокутник, квадрат)
в) тупими. Ні
Завдання 827
На малюнку зображено 8 трикутників: AOB, AOD, DOC, COB, ACD, ABD, ABC, DBC
Завдання 828
Периметр чотирикутника дорівнює 100 см. Три його сторони рівні, кожна з них завдовжки 20 см. Знайди довжину четвертої сторони.
Розв’язання
100 – (20 • 3) = 100 – 60 = 40 (см) – довжина четвертої сторони.
Відповідь: 40 см.
Чи існує такий чотирикутник? Так
Завдання 829
Виріж з паперу довільний трикутник і познач його кути числами: 1, 2, 3. Відірви кути 2 і 3 і приклади до кута 1. Суму трьох кутів трикутника дорівнює 180°.
Завдання 830
Накресли прямокутний і тупокутний трикутники.
|
|
|
Завдання 831
У трикутнику АВС кути А і В дорівнюють 62° і 48°. Зроби малюнок. Знайди кут С.
Розв’язання
180° – (62° + 48°) = 180° – 110° = 70° – кут С.
Відповідь: 70°.
Завдання 832
Один із кутів трикутника дорівнює 37°, а другий — на 27° більший. Знайди міру третього кута.
Розв’язання
1) 37° + 27° = 64° – другий кут;
2) 180° – (37° + 64°) = 180° – 101° = 79° – третій кут.
Відповідь: 79°.
Завдання 833
Один із кутів трикутника дорівнює 96°, а другий у три рази менший. Знайди невідомі кути трикутника.
Розв’язання
1) 96° : 3 = 32° – другий кут;
2) 180° – (96° + 32°) = 180° – 128° = 52° – третій кут.
Відповідь: 32° і 52°.
Завдання 834
Один кут трикутника дорівнює 70°, а два інших — рівні. Знайди міри цих кутів.
Розв’язання
1) 180° – 70° = 110° – сума двох рівних кутів;
2) 110° : 2 = 55° – величина кожного з двох рівних кутів.
Відповідь: 55°.
Завдання 835
Установи вид трикутника, якщо сума двох його кутів дорівнює 74°.
Розв’язання
180° – 74° = 106° – міра третього кута, кут тупий.
Відповідь: тупокутний трикутник.
Завдання 836
Міри двох кутів трикутника дорівнюють 23° і 67°. Який це трикутник?
Розв’язання
180° – (23° + 67°) = 90° – міра третього кута, кут прямий.
Відповідь: прямокутний трикутник.
Завдання 837
Побудуй трикутник АВС, у якого АС = СВ = 5 см і ∠C = 90°.
Як його називають? Рівнобедрений трикутник.
Виміряй і порівняй кути А і В. (180° – 90°) : 2 = 45°, кути рівні, кожен дорівнює 45°.
Завдання 838
Побудуй трикутник KPT, у якого KP = KT = 6 см і ∠K = 120°. Як його називають? Рівнобедрений трикутник.
Виміряй і порівняй його кути Р і Т. (180° – 120°) : 2 = 30°, кути рівні, кожен дорівнює 30°.
Завдання 839
Побудуйте довільний чотирикутник. Виміряйте кожний його кут. Знайдіть їх суму.
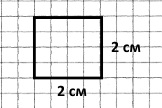
90° + 90° + 90° + 90° = 360° – сума кутів чотирикутника.
Завдання 840
х = 360° – (60° + 150° + 70°) = 300° – 280° = 80°
Завдання 841
Знайди невідомі кути чотирикутника, якщо один із них дорівнює 96°, другий на 12° більший за перший, а третій — у три рази менший за другий.
Розв’язання
1) 96° + 12° = 108° – міра другого кута;
2) 108° : 3 = 36° – міра третього кута;
3) 360° – (96° + 108° + 36°) = 360° – 240° = 120° – міра четвертого кута.
Відповідь: 108°, 36° і 120°.
Завдання 842
У чотирикутнику три кути рівні, а четвертий дорівнює 69°. Знайди кути чотирикутника.
Розв’язання
1) 360° – 69° = 291° – сума трьох рівних кутів;
2) 291° : 3 = 97° – міра кожного з трьох рівних кутів.
Відповідь: 69°, 97°, 97°, 97°.
Завдання 843
Три трикутники: 1 см, 4 см, 5 см; 2 см 4 см 5 см; 3 см, 4 см, 5 см.
Три чотирикутники: 2 см, 3 см, 4 см, 5 см; 1 см, 2 см, 3 см, 4 см; 1 см, 2 см, 3 см, 5 см.
Завдання 844
Знайди міри кутів прямокутного трикутника, якщо найбільший із них у 5 разів більший від найменшого.
Розв’язання
Нехай найменший кут х°, тоді найбільший кут 5х°, а їхня сума 180° – 90° = 90°. Складаємо рівняння.
х + 5х = 90
6х = 90
х = 90 : 6
х = 15° – найменший кут;
15° • 5 = 75° – найбільший кут.
Відповідь: 15° і 75°.
Завдання 845
Один із кутів трикутника дорівнює 60°. Знайди міри двох інших кутів, якщо другий більший за третій на 30°.
Розв’язання
Нехай третій кут х°, тоді другий кут (30 + х)°, а їхня сума 180° – 60° = 120°. Складаємо рівняння.
х + х + 30 = 120
2х + 30 = 120
2х = 120 – 30
2х = 90
х = 90 : 2
х = 45° – третій кут;
15° • 5 = 75° – другий кут.
Відповідь: 45° і 75°.
Завдання 846
Один із кутів трикутника у два рази більший за другий. Знайди кути трикутника, якщо третій кут дорівнює 75°.
Розв’язання
Нехай перший кут х°, тоді другий кут 2х°, а їхня сума 180° – 75° = 105°. Складаємо рівняння.
х + 2х = 105
3х = 105
х = 105 : 3
х = 35° – перший кут;
35° • 2 = 70° – другий кут.
Відповідь: 35° і 70°.
Завдання 847
Один із гострих кутів прямокутного трикутника на 20° більший, ніж другий. Знайди міри цих кутів.
Розв’язання
Нехай другий кут х°, тоді перший кут (х + 20)°, а їхня сума 180° – 90° = 90°. Складаємо рівняння.
х + х + 20 = 90
2х = 90 – 20
2х = 70
х = 70 : 2
х = 35 (°) – другий кут;
35 + 20 = 55 (°) – перший кут.
Відповідь: 35° і 55°.
Завдання 848
Чи може один трикутник мати:
а) два прямих кути; Ні, бо сума всіх кутів трикутника дорівнює 180°
б) два гострих кути; Так, вид такого трикутника гострокутний.
в) один тупий і один прямий кути? Ні, бо 180° – 90° = 90° – сума двох інших кутів.
Завдання 849
Чи може трикутник водночас бути:
а) і прямокутним, і рівнобедреним; Так
б) і прямокутним, і рівностороннім; Ні
в) і тупокутним, і рівнобедреним? Так
Завдання 850
Знайди кути чотирикутника, якщо один із них менший від другого, третього і четвертого, відповідно, на 10°, 20° і 30°.
Розв’язання
Нехай перший кут х°, тоді другий кут (х + 10)°, третій кут (х + 20)°, четвертий кут (х + 30)°, а їхня сума 360°. Складаємо рівняння.
х + (х + 10) + (х + 20) + (х + 30) = 90
4х + 60 = 360
4х = 360 – 60
х = 300 : 4
х = 75 (°) – перший кут;
75 + 10 = 85 (°) – другий кут;
75 + 20 = 95 (°) – третій кут;
75 + 30 = 105 (°) – четвертий кут.
Відповідь: 75°, 85°, 95°, 105°.
Завдання 851
У чотирикутнику ABCD ∠A = ∠C і ∠B = ∠D. Знайди ∠A + ∠B.
Розв’язання
∠A + ∠В + ∠С + ∠D = 360
∠A + ∠В + ∠A + ∠B = 360
2∠A + 2∠В = 360
2(∠A + ∠В) = 360
∠A + ∠В = 360 : 2
∠A + ∠В = 180 (°)
Відповідь: 180°.
Завдання 852
Знайди довжини сторін рівнобедреного трикутника, якщо одна з них на 3 см довша за другу, а периметр трикутника дорівнює 12 см.
Розв’язання
Нехай основа трикутника х см, тоді бічні сторони трикутника (х + 3) см. Складаємо рівняння.
х + (х + 3) + (х + 3) = 12
3х + 6 = 12
3х = 12 – 6
3х = 6
х = 6 : 3
х = 2 (см) – основа трикутника;
2 + 3 = 5 (см) – кожна бічна сторона.
Відповідь: 2 см, 5 см, 5 см.
Завдання 853
Довжини двох сторін трикутника дорівнюють 5 і 8 см. Чи може довжина третьої сторони дорівнювати 15 см? Ні Чому? 5 см + 8 см < 15 см
Завдання 854
Чи існує трикутник, у якого сума двох сторін дорівнює 110 см, а периметр — 224 см? Ні
224 см – 110 см = 114 см – третя сторона.
110 см < 114 см
Завдання 855
Чи існує чотирикутник зі сторонами 2, 3, 4 і 10 м? Ні Чому? 2 м + 3 м + 4 м < 10 м
Завдання 856
В Олі та Колі було порівну марок. Оля віддала Колі 5 марок. У кого стало марок більше і на скільки?
Розв’язання
х – 5 = х + 5
х = х + 5 + 5
х = х + 10
Відповідь: на 10 марок більше стало більше марок у Колі.
Завдання 857
Переклади один сірник так, щоб стала правильною рівність. VI – IV = II
Завдання 858
Сума двох чисел дорівнює 418. Одне з них закінчується нулем. Якщо цей нуль закреслити, то вийде друге число. Які це числа?
Розв’язання
Нехай менше число х, тоді більше число 10х. Складаємо рівняння.
х + 10х = 418
11х = 418
х = 418 : 11
х = 38 – менше число;
38 • 10 = 380 – більше число.
Відповідь: 38 і 380.
Вправи для повторення
Завдання 859
Для кожної нерівності добери по два значення x, щоб нерівність була правильною:
а) x – 32 < 15, x < 15 + 32, x < 47, якщо х = 45, 46
б) 3x > 19, якщо х = 7, 8
Завдання 860
Стрічку завдовжки 5 м розрізали на три частини, одна з яких виявилася утричі довшою за кожну з інших. Знайди довжину кожної частини.
Розв’язання
Нехай довжина менших сторін х м, тоді найбільша сторона 3х. Складаємо рівняння.
х + х + 3х = 5
5х = 5
х = 5 : 5
х = 1 – менші сторони;
1 • 3 = 3 – більша сторона.
Відповідь: 1 м, 1 м і 5 м.
Завдання 861
Дванадцять футбольних команд зіграли кожна з кожною по 2 рази. Скільки всього відбулося ігор? 12 • 11 = 132 зустрічі.