Завдання 1193
Правильна підстановка для системи рівняннь x = 7y – 5, 2x + 3y = 9?
|
1) 2x + 3(7y – 5) = 9 |
2) 2 + (7y – 5) + 3y = 9 |
3) 2(7y – 5) + 3y = 9 |
Завдання 1194
Правильна підстановка для системи рівнянь y = 4x + 3, 7x + 2y = 9?
|
1) 7(4 x + 3) + 2y = 9 |
2) 7x + 2 – (4 x + 3) = 9 |
3) 7x + 2(4x + 3) = 9 |
Завдання 1195 Розв'язування способом підстановки
|
1) {7x = 21 2x – 3y = 3 x = 21 : 7 х = 3 2 • 3 – 3y = 3 6 – 3y = 3 –3y = –3 y = 1 Відповідь: (3;1) |
2) {6x – y = 17 –2y = 10 y = 10 : (–2) y = –5 6x – (–5) = 17 6x + 5 = 17 6x = 12 x = 2 Відповідь: (2;–5) |
Завдання 1196
|
1) {x = y + 2 4x – 8y = 20 4(y + 2) – 8y = 20 4y + 8 – 8y = 20 –4y = 12 y = –3 x = –3 + 2 = –1 Відповідь: (–1;–3) |
2) {y = x – 3 5x + 2y = 29 5x + 2(x – 3) = 29 5x + 2x – 6 = 29 7x = 35 x = 5 y = 5 – 3 = 2 Відповідь: (5;2) |
Завдання 1197 Розв'язок системи рівнянь
|
1) {–4x = 8 5x – 2y = 4 x = 8 : (–4) x = –2 5 • (–2) – 2y = 4 –2y = 14 y = –7 Відповідь: (–2;–7) |
2) {y = x + 5 7x + 3y = –5 7x + 3(x + 5) = –5 7x + 3x + 15 = –5 10x = –20 x = –2 y = –2 + 5 = 3 Відповідь: (–2;3) |
Завдання 1198
|
1) {x + y = 7 2x + y = 9 x = 7 – y 2(7 – y) + y = 9 14 – 2y + y = 9 y = 5 x = 7 – 2 = 5 Відповідь: (2;5) |
2) {x – y = –2 x – 2y = 5 x = y – 2 (y – 2) – 2y = 5 y – 2 – 2y = 5 –y = 7 y = –7 x = –7 – 2 = –9 Відповідь; (–9;–7) |
3) {y – x = 0 4x + y = 15 y = x 4x + x = 15 5x = 15 x = 3 y = 3 Відповідь: (3;3) |
|
4) {5x + 2y = 2 x – 2y = 10 x = 10 + 2y 5(10 + 2y) + 2y = 2 50 + 10y + 2y = 2 12y = –48 y = –4 x = 10 + 2 • (–4) = 2 Відповідь: (2;–4) |
5) {x – 3y = 7 2x – 3y = –3 x = 7 + 3y 2(7 + 3y) – 3y = –3 14 + 6y – 3y = –3 3y = –17 y = –17/3 = –5 2/3 x = 7 + 3 • (–17/3) = –10 Відповідь: (–10;–5 2/3) |
6) {5x – 3y = –19 2x + y = –1 y = –1 – 2x 5x – 3(–1 – 2x) = –19 5x + 3 + 6x = –19 11x = –22 x = –2 y = –1 – 2 • (–2) = 3 Відповідь: (–2;3) |
Завдання 1199 Розв'язування способом підстановки
|
1) {x + y = 4 3x + y = 6 y = 4 – x 3x + (4 – x)=6 3x + 4 – x = 6 2x = 2 x = 1 y = 4 – 1 = 3 Відповідь: (1;3) |
2) {x – y = 0 x – 2y = 8 x = y y – 2y = 8 –y = 8 y = –8 x = –8 Відповідь:(–8;–8) |
3) {y – x = –5 2x + y = 4 y = x – 5 2x + (x – 5)=4 2x + x – 5 = 4 3x = 9 x = 3 y = 3 – 5 = –2 Відповідь: (3;–2) |
4) {3x – 2y = 6 x + 2y = 2 x = 2 – 2y 3(2 – 2y) – 2y=6 6 – 6y – 2y = 6 –8y = 0 y = 0 x = 2 – 2 • 0 = 2 Відповідь: (2;0) |
Завдання 1200, 1201
Не виконуючи побудови, знайдіть координати точки перетину графіків рівнянь.
|
{x + y = 4 3x + y = 6 y = 4 – x 3x + (4 – x)=6 3x + 4 – x = 6 2x = 2 x = 1 y = 4 – 1 = 3 Відповідь: (1;3) |
{x – y = 3 3x + 2y = 14 x = y + 3 3(y + 3) + 2y = 14 3y + 9 + 2y = 14 5y = 5 y = 1 x = 3 + 1 = 4 Відповідь: (4;1) |
Завдання 1202 Розв'язування способом підстановки
|
1) {3х + 4у = 0 2х – 7у = 29 у = –3/4 x 2x – 7 • (–3/4 x) = 29 2x + 21/4 x = 29 |•4 8x + 21х = 116 29x = 116 x = 4 у = –3/4 • 4 = –3 Відповідь: (4;–3) |
2) {8x – 5у = 41 4х + 3у = –7 {8x – 5у = 41 3у = –4х – 7 у = (–4x – 7)/3 8x – 5 • (–4x – 7)/3 = 41 8x – (–20x – 35)/3 = 41 |•3 8x – (–20x – 35) = 123 24x + 20x + 35 = 123 44x + 35 = 123 44x = 88 x = 2 у = (–4 • 2 – 7)/3 = –15/3 = –5 Відповідь: (2;–5) |
|
3) {2а – 5b = 0 –7а + 4b = 27 b = 2/5 a –7a + 4 • 2/5 a = 27 –7a + 8/5 a = 27 |•5 –35a + 8a = 135 –27a = 135 a = –5 b = 2/5 • (–5) = –2 Відповідь: (–5;–2) |
4) {10m – 2n = 39 9m + 4n = 38 n = (10m – 39)/2 9m + 4 • (10m – 39)/2 =38 9m + (40m – 156)/2 = 38 |•2 18m + 40m – 156 = 76 58m – 156 = 76 58m = 232 m = 4 n = (10 • 4 – 39)/2 = 1/2 = 0,5 Відповідь: (4;0,5) |
Завдання 1203
|
1) {4х + Зу = 0 5x – 7у = –43 у = –4/3 x 5x – 7 • (–4/3 x) = –43 5x + 28/3 x = –43 |•3 15x + 28x = –129 43x = –129 x = –3 у = –4/3 • (–3) = 4 Відповідь: (–3;4) |
2) {2х + 9у = –59 5x – 4у = 38 у = (–59 – 2x)/9 5x – 4 • (–59 – 2x)/9 = 38 5x – (–236 – 8x)/9 = 38 |•9 5x – (–236 – 8x) = 342 45x + 236 + 8x = 342 53x = 106 x = 2 у = (–59 – 2 • 2)/9 = –63/9 = –7 Відповідь: (2;–7) |
|
3) {Зр – 7q = 0 2p + 9q = 41 {7q = Зр 2p + 9q = 41 q = 3/7 p 2p + 9 • 3/7 p = 41 2p + 27/7 p = 41 |•7 14p + 27p = 281 41p = 287 p = 7 q = 3/7 • 7 = 3 Відповідь: (7;3) |
4) {6а – 7b = 51 2а + 3b = –15 {7b = 6a – 51 2а + 3b = –15 b = (6a – 51)/7 2a + 3 • (6a – 51)/7 = –15 2a + (18a – 153)/7 = –15 |•7 14a + 18a – 153 = –105 32a – 153 = –105 32a = 48 a = 1,5 b = (6 • 1,5 – 51)/7 = –42/7 = –6 Відповідь: (1,5;–6) |
Завдання 1204 Розв'язок системи
|
1) {7(х – 3) + 8 = 4 + 5x 4(x – y) – 7y = 6,5 {7х – 21 + 8 = 4 + 5x 4x – 4y – 7y = 6,5 {7х – 5x = 4 + 21 – 8 4x – 4y – 7y = 6,5 {2x = 17 4x – 11y = 6,5 х = 17 : 2 x = 8,5 4 • 8,5 – 11y = 6,5 34 – 11y = 6,5 11y = 27,5 y = 2,5 Відповідь: (8,5;2,5) |
2) {4(x + y) – 3y = 2 9(x – 2y) – 6x = –11 {4x + 4y – 3y = 2 9x – 18y – 6x = –11 {4x + y = 2 3x – 18y = –11 y = 2 – 4x 3x – 18 • (2 – 4x) = –11 3x – 36 + 72x = –11 3x + 72x = 36 – 11 75x = 25 x = 1/3 y = 2 – 4•1/3 = 2 – 1 1/3 = 1 3/3 – 1 • 1/3 = 2/3 Відповідь: (1/3;2/3) |
Завдання 1205
|
1) {4(x + y) – 8y = –4 7(y + 1) – (y + 3) = 19 {4x + 4y – 8y = –4 7y + 7 – y – 3 = 19 {4x = 4y – 4 |:4 7y – y = 19 + 3 – 7 {x = y – 1 6y = 15 у = 2,5 х = 2,5 – 1 = 1,5 Відповідь: (1,5;2,5) |
2) {8(x + y) – 12y = 6 6(3x – y) + 18x = 13 {8x + 8y – 12y = 6 18x – 6y + 18x = 13 {4у = 8x – 6 |:2 36х – 6y = 13 {2у = 4x – 3 36х – 6y = 13 y = (4x – 3)/2 36х – 6 • (4x – 3)/2 = 13 36х – (24x – 18)/2 = 13 |•2 72х – (24x – 18) = 26 72х – 24x + 18 = 26 48x = 8 x = 8/48 = 1/6 y = (4/6 – 3)/2 = (2/3 – 2 3/3)/2 = = –2 1/3 : 2 = –7/3 • 1/2 = –7/6 = –1 1/6 Відповідь: (1/6;–1 1/6) |
Завдання 1206
|
1) {1/8(x – y) = 9 |•8 1/3(x + y) = 7 |•3 {x – y = 72 x + y = 21 x = y + 72 y + 72 + y = 21 2у = 21 – 72 2у = –51 y = –25,5 x = –25,5 + 72 = 46,5 Відповідь: (46,5;–25,5) |
2) {0,2(2x + у) = З |•5 0,7(x – 4у) = –1,05 |:0,7 {2x + y = 15 x – 4y = –1,5 y = 15 – 2x x – 4(15 – 2x) = –1,5 x – 60 + 8x = –1,5 9x = 58,5 x = 6,5 y = 15 – 2 • 6,5 = 15 – 13 = 2 Відповідь: (6,5;2) |
Завдання 1207
|
1) {0,4(x + у) = 12 |:0,4 0,6(x – у) = 9 |:0,6 {x + y = 30 x – y = 15 y = 30 – x x – 30 + x = 15 2x = 45 x = 22,5 y = 30 – 22,5 = 7,5 Відповідь: (22,5;7,5) |
2) {1/7(2x + у) = 13 |•7 1/3(x – Зу) = 14 |•3 {2x + y = 91 x – 3y = 42 y = 91 – 2x x – 3(91 – 2x) = 42 x – 273 + 6x = 42 x = 45 y = 91 – 2 • 45 = 91 – 90 = 1 Відповідь: (45;1) |
Завдання 1208, 1209
|
{(x + 1)/5 + (y – 1)/3 = 1 |•15 (x + 2)/6 + (y + 2)/3 = 2 |•6 {3(x + 1) + 5(y – 1) = 15 x + 2 + 2(y + 2) = 12 {3x + 3 + 5y – 5 = 15 x + 2 + 2y + 4 = 12 {3x + 5y = 17 x + 2y = 6 x = 6 – 2y 3(6 – 2y) + 5y = 17 18 – 6y + 5y = 17 y = 1 x = 6 – 2 • 1 = 6 – 2 = 4 Відповідь: (4;1) |
{(x – 4)/2 + (y + 11)/4 = 1 |•4 (x + 7)/3 + (y – 4)/7 = 2 |•21 {2(x – 4) + y + 11 = 4 7(x + 7) + 3(y – 4) = 42 {2x – 8 + y + 11 = 4 7x + 49 + 3y – 12 = 42 {2x + y = 1 7x + 3y = 5 y = 1 – 2x 7x + 3(1 – 2x) = 5 7x + 3 – 6x = 5 x = 2 y = 1 – 2 • 2 = 1 – 4 = –3 Відповідь: (2;–3) |
Завдання 1210
Доведіть, що графіки рівнянь 2x – 3у = 4 і 4x – 6у = 9 є паралельними прямими.
{2x – 3у = 4
4x – 6у = 9
x = (4 + 3y)/2
4(4 + 3y)/2 – 6y = 9
8 + 6y – 6y = 9
8 = 9 – рівність неправильна, система рівнянь не має розв’язку, тому графіки не перетинаються, а отже є паралельними прямими.
Завдання 1211
Графік функції y = kx + l проходить через точки М(9;1) і N(–6;–4). Знайдіть k і l.
{9k + l = 1
–6k + l = –4
l = 1 – 9k
–6k + 1 – 9k = –4
–15k = –5
k = 1/3
l = 1 – 9 • 1/3 = 1 – 3 = –2
Завдання 1212
Графіком функції y = kx + l є пряма, що проходить через точки A(–2;–4) і B(4;11). Задайте цю функцію формулою.
{–2k + l = –4
4k + l = 11
l = –4 + 2k
4k – 4 + 2k = 11
6k = 15
k = 2,5
l = –4 + 2 • 2,5 = –4 + 5 = 1
Формула функції: у = 2,5х + 1
Завдання 1213
|
1) {2х + у = 8 4x + my = 10 |:2 {2х + у = 8 2x + m/2 y = 5 Система не має розв'язків, коли вираз одночасно набуває різних значень: m/2 = 1, тому при m = 2 |
2) {х – 3у = 5 mх – 12у = 20 |:4 {х – 3у = 5 m/4 х – 3у = 5 Система має безліч розв'язків, коли вираз одночасно набуває однакових значень: m/4 = 1, тому при m = 4 |
Вправи для повторення
Завдання 1214
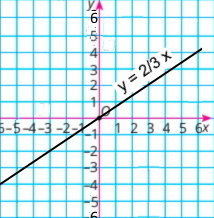
Побудуйте графік функції, заданої формулою y = 2/3x.
|
y = 2/3x |
|
|
1) якщо x = –6, то у = –4; якщо х = 0, то у = 0; якщо х = 3, то у = 2.
2) у = –2, якщо х = –3; у = 0, якщо х = 0; у = 4, якщо х = 6
Завдання 1215 Розкладання на множники многочлена
1) 9m2 + 12m5 – 18m3 = Зm2(3 + 4m3 – 6m)
2) 3x4y² – 9х²y3 + 12x3y = Зх²у(x²у – Зу² + 4х)
3) а6 – 6 – 2а² + 3а4 = (а6 – 2a²) + (За4 – 6) = а²(а4 – 2) + 3(а4 – 2) = (a4 – 2)(a² + 3)
4) рq – 6р + р² – 6q = (pq + р²) – (6р + 6q) = p(q + р) – 6(q +р) = (q + р)(р – 6)
Завдання 1216
Доведіть, що рівняння не має розв'язків:
1) Рівняння x² + 4 = 0
Не має розв’язків, бо сума невід’ємного і додатного чисел не може дорівнювати нулю;
2) x² – 6х + 13 = 0
x² – 6х + 9 + 4 = 0
(х – 3)² + 4 = 0
Не має розв’язків, бо сума невід’ємного і додатного чисел не може дорівнювати нулю;
3) 4x² – 12х + 16 = 0
4х² – 12х + 9 + 7 = 0
(2х – 3)² + 7 = 0
Не має розв’язків, бо сума невід’ємного і додатного чисел не може дорівнювати нулю;
4) x² + x + 2 = 0
x² + x + 1/4 + 1 3/4 = 0
(х + 1/2)² +1 3/4 = 0
Не має розв’язків, бо сума невід’ємного і додатного чисел не може дорівнювати нулю.
Завдання 1217
Під час чищення зубів мати витрачає воду економно (доки чистить зуби, кран закручує), а батько цього не робить. За показниками лічильника води діти встановили, що мати витрачає щоранку 1,5 л води, а батько – вдвічі більше.
1) На скільки літрів води щомісяця більше витрачає батько, ніж мати?
Примітка. Обрахунки проводимо без врахування кількості разів чищення зубів на добу.
1,5 • 2 = 3 (л) – витрачає води щодня батько;
3 – 1,5 = 1,5 (л) – на стільки води щодня більше витрачає батько, ніж мати.
1,5 • 30 = 45 (л) – на стільки води щомісяця більше витрачає батько, ніж мати.
Відповідь: на 45 л.
2) Практична діяльність. Дізнайтеся, скільки коштує 1 м3 води у вашій місцевості, та визначте, скільки коштів може заощадити ця родина за місяць (30 днів), якщо батько під час чищення зубів також буде економно витрачати воду.
Вода 1 м3 = 1000 л і коштує 25,88 грн в місяць.
1000 л — 25,88 грн
45 л — х грн
1000/45 = 25,88/х; х = 25,88 • 45 : 1000 = 1,16 (грн) – заощадить ця родина на місяць.
Відповдіь: 1,16 грн.
Завдання 1218
Якщо добуток чотирьох послідовних натуральних чисел збільшити на 1, то він дорівнюватиме квадрату деякого натурального числа. Доведіть це.
Розв'язання
Нехай х, х + 1, х + 2 і х + 3 — чотири послідовні натуральні числа.
Розглянемо їх добуток, збільшений на 1.
х(х + 1)(х + 2)(х + 3) + 1 = х(х + 3)(х + 1)(х + 2) + 1 = (х² + Зх)((х² + Зх) + 2) + 1 =
= (х² + Зх)² + 2(х² + Зх) + 1 = (х² + Зх + 1)², що й треба було довести.