Інша завдання дивись тут...

Завдання 1012

1) За графіком на малюнку 23.7 заповнили таблицю:

х	–3	–2,5	–2	–1,5	–0,5	0	1	2	3
у	–1,5	–1	0	1	1,5	2,5	2	2,5	3

2) область визначення функції: –3 ≤ x ≤ 3; область значень функції: –1,5 ≤ y ≤ 3.

 

Завдання 1013

1) За графіком На малюнку 23.8 заповнили таблицю:

х	–2	–1,5	–1	–0,5	0	0,5	1	1,5	2	2,5	3	3,5	4
у	1	0,5	1,5	2	1,5	0	–1	–1,5	–1	–2	–3	–2,5	–2

2) область визначення функції: –2 ≤ x ≤ 4; область значень функції: –2 ≤ y ≤ 1

 

Завдання 1014

Для функції y = x – 3, де –2 ≤ x ≤ 5 склали таблицю для цілих значень аргументу.

x	–2	–1	0	1	2	3	4	5
y	–5	–4	–3	–2	–1	0	1	2

Побудували графік функції y = x – 3

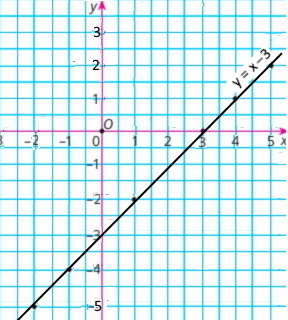
1) Точка A(3;0) належить графіку; точка B(–1;2) не належить графіку;

2) Якщо x = 2, то y = –1; якщо x = 4, то y = 1

3) y = –3, якщо x = 0; y = 2, якщо x = 5

 

Завдання 1015

Для функції y = x + 2, де –4 ≤ x ≤ 3 склали таблицю для цілих значень аргументу.

x	–4	–3	–2	–1	0	1	2	3
y	–2	–1	0	1	2	3	4	5

Побудували графік функції y = x + 2

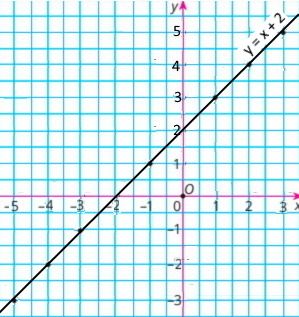
1) Точка C(2; 5) не належить графіку; точка D(–2; 0) належить графіку;

2) Якщо x = –3, то y = –1; якщо x = 1, то y = 3

3) y = 1, якщо x = –1; y = 5, якщо x = 3

 

Завдання 1016 Нулі функції

1) y = 5x; у = 0, якщо 0 = 5х; х = 0

2) y = 3x – 6; y = 0, якщо 0 = 3х – 6; 3x = 6; x = 2

3) y = –x/10; у = 0, якщо 0 = –x/10; х = 0

4) y = (5 – x)/8. y = 0, якщо 0 = (5 – x)/8; 0 = 5 – x; x = 5

 

Завдання 1017

1) y = –3x; y = 0, якщо 0 = –3х; х = 0

2) y = 12 – 4x; y = 0, якщо 0 = 12 – 4x; 4x = 12; х = 3

3) у = x/3; y = 0, якщо 0 = x/3; х = 0

4) у = (x + 2)/4.  y = 0, якщо 0 = (x + 2)/4; х + 2 = 0; х = –2

 

Завдання 1018

Визнач за графіком.

1) Температура повітря о 3 год була –5,5°С, о 5 год: –5,2°С, о 7 год: –2°С,

о 21 год: –2 °С;

2) температура повітря –5°С була о 2 год 15 хв і о 5 год 15 хв; 0°С — о 8 год і о 20 год;

5 °С — о 14 год.

 

Завдання 1019

Визнач за графіком.

1) Температура повітря в 0 год –З °С, о 2 год –5°С, о 9 год 1,2 °С, о 12 год З °С,

о 18 год 1 °С;

2) температура повітря була –6 °С о 4 год і 24 год; –2°С о 7 год і 21 год;

1 °С о 8 год 40 хв і 18 год; З °С о 12 год і 16 год;

3) найнижча температура –6 °С була о 4 год і 24 год;

4) найвища температура 5 °С була о 14 год;

5) температура повітря підвищувалась від 4 год до 14 год;

6) температура повітря знижувалась від 0 год до 4 год і від 14 год до 24 год;

7) температура повітря була нижча 0 °С від 0 год до 8 год і від 20 год до 24 год;

8) температура повітря була вища 0 °С від 8 год до 20 год.

 

Завдання 1020

Визнач за графіком.

1) Якщо х = –3, то у = –2; якщо х = –2, то у = –2,5; якщо х = –0,5, то у = 1; якщо х = 1,5, то

у = 2,5; якщо х = 4, то у = –1;  

2) у = –2,5, якщо х = –2; у = –1,5, якщо х = –1,5 або х = 3,5; у = 1, якщо х = –0,5 або

х = 2,5; 

3) нулі функції: х = –1 і х = 3

4) функція набуває додатних значень, якщо –1 < х < 3;

5) функція набуває від’ємних значень, якщо –3 ≤ х < –1 і 3 < х ≤ 4.

 

Завдання 1021

Визнач за графіком.

1) Якщо х = –3,5, то у = 2; якщо х = –2, то у = 2; якщо х = –1,5, то у = 1; якщо х = 0, то

у = –2; якщо х = 1, то у = –1,5; якщо х = 2,5, то у = 1;

2) у = –1, якщо х = –0,5 або х= 1,5; у = 1, якщо х = –1,5 або х = 2,5; у = 2, якщо

х = –3,5 або х = –2 або х = 3; у = 3, якщо х = 4;

3) нулі функції: х = –1 і х = 2

4) функція набуває від’ємних значень, якщо –1 < х < 2;

5) функція набуває додатних значень, якщо –4 ≤ х < –1 і 2 < х ≤ 4.

 

Завдання 1022

Не виконуючи побудови, з'ясуйте, чи належить графіку функції y = x² – 3x точка:

1) (1; –2); Належить, бо –2 = 1² – 3 • 1; –2 = –2 — правильна рівність;

2) (–2; –2); Не належить, бо –2 = (–2)² – 3 • (–2); –2 = 10 — неправильна рівність;

3) (0; –3); Не належить, бо –3 = 0 – 3 • 0; –3 = 0 — неправильна рівність;

4) (–1; 4). Належить, бо 4 = (–1)² – 3 • (–1); 4 = 4 — правильна рівність.

 

Завдання 1023

Не виконуючи побудови графіка функції y = 2x + x² , з'ясуйте, чи належить йому точка:

1) (1; 3); Належить, бо 3 = 2 • 1 + 1; 3 = 3 —правильна рівність;

2) (–1; 3); Не належить, бо: 3 = 2 • (–1) + (–1)²; 3 = –1 — неправильна рівність;

3) (0; 0); Належить, бо 0 = 2 • 0 + 0; 0 = 0 — правильна рівність;

4) (–2; 4). Не належить, бо 4 = 2 • (–2) + (–2)²; 4 = 0 — неправильна рівність.

 

Завдання 1024

Ламана ABC – графік деякої функції, причому A(–3; 2), B(1; 6), C(4; 0).

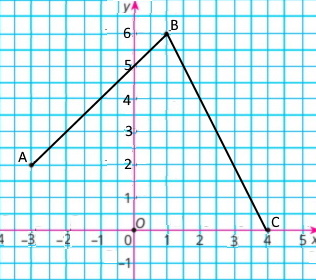
1) Якщо х = –2, то у = 3; якщо x = 0, тo y = 5; якщо х = 1, то у = 6;

2) у = 2, якщо x = –3 і х = 3; у = 4, якщо x = –1 і х = 2; у = 6, якщо х = 1.

 

Завдання 1025

Ламана MNL є графіком деякої функції, причому M(–2; –1), N(2; 3), L(6; –1).

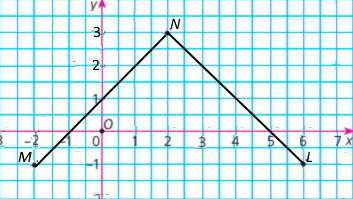
1) Якщо х = –2, то у = –1; якщо x = 0, то у = 1; якщо х = 2, то у = 3; якщо х = 5, то y = 0;

2) у = –1, якщо x = –2 і x = 6; у = 1, якщо x = 0 і x = 4; у = 3, якщо x = 2.

 

Завдання 1026

Не будуючи графіка, знайдіть нулі функції:

1) y = x² – 4x 0 = x² – 4x x(x – 4) = 0 x = 0 або x – 4 = 0 x = 0        х = 4

2) y = 16 – x² 0 = 16 – х² (4 – x) (4 + x) = 0 4 – x = 0 або 4 + x = 0 x = 4            х = –4

3) y = 2x² + 10x. 0 = 2x² + 10x 2x(x + 5) = 0 2x = 0 або x + 5 = 0 x = 0        x = –5

Завдання 1027

Не будуючи графіка, знайдіть нулі функції:

1) y = x² + 2x x² + 2x = 0 x(x + 2) = 0 x = 0 або x + 2 = 0 x = 0        х = –2

2) y = x² – 25 x² – 25 = 0 (х – 5)(x + 5) = 0 x – 5 = 0 або x + 5 = 0 x = 5           x = –5

3) y = 12x – 3x² 12x – 3x² = 0 3x(4 – x) = 0 х = 0 або 4 – х = 0 x = 0        х = 4

Завдання 1028

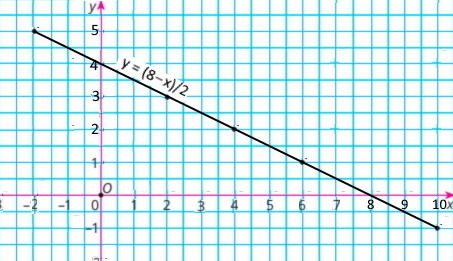
1) Для функції y = (8 – x)/2, де –2 ≤ x ≤10 склали таблицю для цілих значень аргументу.

x	–2	0	2	4	6	8	10
y	5	4	3	2	1	0	–1

Побудували графік функції y = (8 – x)/2

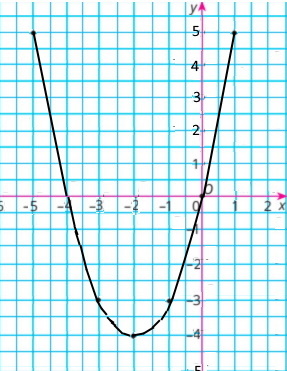
2) для функції y = x(4 + x), де –5 ≤ x ≤ 1 склали таблицю для цілих значень аргументу.

x	–5	–4	–3	–2	–1	0	1
y	5	0	–3	–4	–3	0	5

Побудували графік функції y = x(4 + x)

Завдання 1029

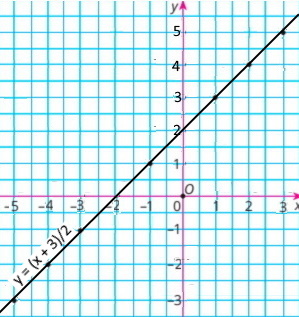
1) для функції у = (x + 3)/2, де –5 ≤ x ≤ 7 склали таблицю для цілих значень аргументу.

x	–5	–4	–3	0	1	3	5	7
y	–1	–0,5	0	1,5	2	3	4	5

Побудували графік функції у = (x + 3)/2

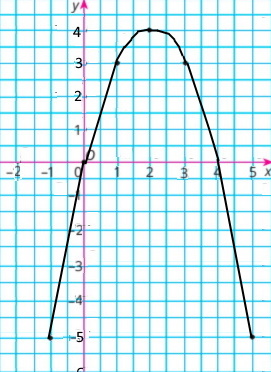
2) для функції y = x (4 – x), де –1 ≤ x ≤ 5 склали таблицю для цілих значень аргументу.

x	–1	0	1	2	3	4	5
y	–5	0	3	4	3	0	–5

Побудували графік функції y = x(4 – x)

Завдання 1030

Лінія, зображена на малюнку 23.11, не є графіком функції, бо, наприклад, якщо х = 0, то у набуває кількох значень. 

 

Завдання 1031

На малюнку 23.12 зображено графік залежності маси m (у кг) відра з водою від об'єму V (у л) води в ньому. Знайдіть за графіком:

1) Маса порожнього відра дорівнює 2 кг;

2) маса відра з 4л води дорівнює 6 кг;

3) маса одного літра води дорівнює: 3 – 2 = 1 (кг);

4) якщо маса відра з водою дорівнює 8 кг, то об'єм води у відрі – 6 л.

 

Завдання 1032 Спрощення виразу

1) (а – 5)(а + 5) – а(а + 7) = a² – 25 – a² – 7а = –7a – 25

2) m(m – 4) + (9 – m)(m + 9) = m² – 4m + 81 – m² = 81 – 4m

3) 2а (а – b) – (а – b)² = (а – b)(2а – а + b) = (а – b)(а + b) = а² – b²

4) (q + 5р)(5р – q) – (p – 5q)² – 10pq = 25р² – q² – р² + 10pq – 25q² – 10pq = 24p² – 26q²

 

Завдання 1033 Ознака подільності числа

Доведіть, що різниця між будь–яким трицифровим натуральним числом і сумою його цифр кратна числу 9. Нехай трицифрове натуральне число дорівнює 100x + 10y + z, тоді сума його цифр — x + y + z. Маємо: (100x + 10y + z) – (x + y + z) =

= 100x + 10y + z – x – y – z = 99х – 9у = 9(11x – у) — ділиться націло на 9.

 

Завдання 1034

1) Використання проточної води для миття посуду чи прання білизни призводить до марних витрат води в середньому до 15 л за хвилину. Скільки води можна зберегти під час півгодинного прання, якщо правильно ставитися до споживання води?

Розв'язання

15 : 2 = 7,5 (л) – можна зберегти води під час півгодинного прання.

Відповідь: 7,5 л.

2) Практична діяльність. З'ясуйте, який тариф на воду (ціна за 1 м³ води) у вашій місцевості, та обчисліть, скільки коштів за годину можна заощадити, якщо правильно ставитися до споживання води.

Розв'язання

15 • 60 : 1000  • 25,10 = 21,59 (грн) – можна заощадити грошей.

Відповідь: 22,59 грн.

 

Завдання 1035

Доведіть, що якщо n – натуральне число (n > 1), то число 4ⁿ – 3 не може бути квадратом натурального числа.

Припустимо, що 4ⁿ – 3 є квадратом натурального числа. Тоді 4ⁿ – 3 = а²; (2ⁿ)² – 3 = a².

Звідси (2ⁿ)² – а² = 3; (2ⁿ – а)(2ⁿ + а) = 3. Дана рівність має місце для натуральних n лише

тоді, коли 2ⁿ – a = 1, 2ⁿ + a = 3. одержимо: 2 • 2ⁿ = 4; 2ⁿ = 2, що можливо, лише коли

n = 1, що суперечить умові.

Інша завдання дивись тут...