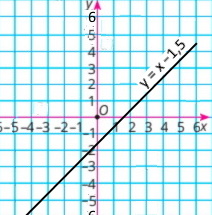
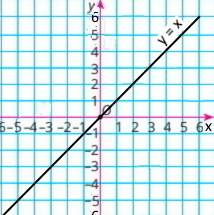
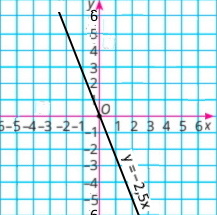
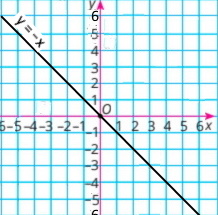
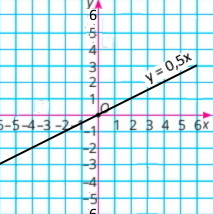
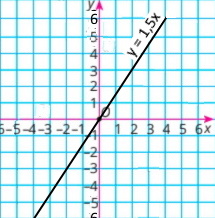
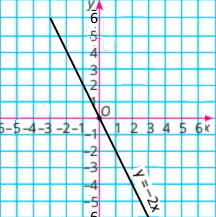
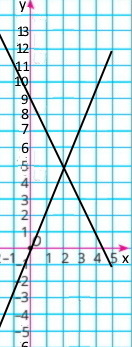
Завдання 1036 Лінійна функція
|
1) y = 2x – 3; Так 4) у = 4/x; Ні |
2) y = 4x – x²; Ні 5) y = x/3 – 1; Так |
3) y = 3; Так 6) y = x – 1 – x6. Ні |
Завдання 1037
|
1) y = 2x² – 7; Ні 4) у = x/2 + 3; Так |
2) y = 3x – 1; Так 5) y = –4; Так |
3) y = 10/x; Ні 6) y = 7x – x3. Ні |
Завдання 1038 Пряма пропорційність
|
1) y = 2х; Так 4) у = 2; Ні |
2) у = 2/х; Ні 5) y = –x/2; Так |
3) у = х + 2; Ні 6) y = x/2; Так |
Завдання 1039
|
1) у = –3х; Так 4) у = –3; Ні |
2) у = –3х + 1; Ні 5) у = x/3; Так |
3) у = –3/х; Ні 6) у = –x/3; Так |
Завдання 1040
Лінійна фукнція задається загальною формулою у = kx + l.
1) для функції у = –0,8х + 7 коефіцієнт k = –0,8, а коефіцієнт l = 7;
2) для функції у = 6 – х коефіцієнт k = –1, а коефіцієнт l = 6;
3) для функції y = x/3 коефіцієнт k = 1/3, а коефіцієнт l = 0;
4) для функції у = 2,4х коефіцієнт k = 2,4, а коефіцієнт l = 0;
5) для функції у = –15 коефіцієнт k = 0, а коефіцієнт l = –15;
6) для функції у = 0 коефіцієнт k = 0, а коефіцієнт l = 0.
Завдання 1041
Ширина прямокутника дорівнює x см, а його довжина на 3 см більша за ширину.
1) Залежність периметра прямокутника від його ширини можна задати формулою:
P = 2(х + х + 3) = 4х + 6, яка є лінійною функцією;
2) залежність площі прямокутника від його ширини можна задати формулою:
S = х • (х + 3) = x² + Зх, яка не є лінійною функцією.
Завдання 1042
Учениця купила щоденник за 15 грн і кілька зошитів по 4 грн. Задайте формулою залежність вартості покупки y (у гривнях) від кількості придбаних зошитів x. Чи є ця залежність лінійною функцією? Якою є область визначення цієї функції?
Формула у = 15 + 4х. Ця залежність є лінійною функцією. Область визначення цієї функції складають натуральні числа.
Завдання 1043
Учень мав 30 грн. За ці кошти він придбав x олівців, по 1,5 грн кожен, після чого в нього залишилося y грн. Задайте формулою залежність y від x. Чи є ця залежність лінійною функцією?
Формула у = 30 – 1,5х. Ця залежність є лінійною функцією.
Завдання 1044
Лінійну функцію задано формулою y = 0,5x + 3. Знайдіть значення у:
1) якщо х = –12, тоді у = 0,5 • (–12) + 3 = –6 + 3 = –3;
якщо х = 0, тоді у = 0,5 • 0 + 3 = 0 + 3 = 3;
якщо х = 18, тоді у = 0,5 • 18 + 3 = 9 + 3 = 12;
2) у = –4, якщо –4 = 0,5х + 3; 0,5х = –7; х = –14;
у = 8, якщо 8 = 0,5х + 3; 0,5х = 5; х = 10;
у = 2,5, якщо 2,5 = 0,5х + 3; 0,5х = –0,5; х = –1.
Завдання 1045
Дано лінійну функцію y = –2x + 3. Знайдіть значення у:
1) якщо х = 1,5, тоді у = –2 • 1,5 + 3 = –3 + 3 = 0;
якщо х = –4, тоді у = –2 • (–4) + 3 = 8 + 3= 11;
якщо х = –6,5, тоді у = –2 • (–6,5) + 3 = 13 + 3 = 16;
2) у = 5, якщо 5 = –2х + 3; –2х = 2; х = –1;
у = 0, якщо 0 = –2х + 3; –2х = –3; х = 1,5;
у = –8, якщо –8 = –2х + 3; –2х = –11; х= 5,5.
Завдання 1046
Використовуючи графік функції на малюнку, заповніть у зошиті таблицю:
|
x |
–2 |
0 |
1 |
3 |
–3 |
–1 |
2 |
|
y |
–3 |
1 |
3 |
7 |
–5 |
–1 |
5 |
Завдання 1047
Використовуючи графік функції на малюнку, заповніть у зошиті таблицю:
|
x |
–6 |
–2 |
2 |
8 |
4 |
–4 |
|
y |
4 |
2 |
0 |
–3 |
–1 |
3 |
Завдання 1048
Запишіть координати будь–яких двох точок, що належать графіку функції у = 5х – 2.
Якщо х = 0, тоді у = 5 • 0 – 2 = –2, тому графіку належить точка A(0;–2)
Якщо х = 1, тоді у = 5 • 1 – 2 = 3, тому графіку належить точка В(1;3)
Завдання 1049
Заповніть у зошиті таблицю значень лінійної функції та побудуйте її графік:
|
1) у = –х + 2
|
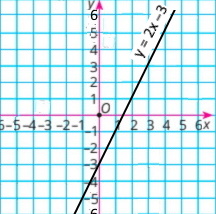
2) у = 2х – 3
|
||||||||||||
|
|
 |
Завдання 1050
Заповніть у зошиті таблицю значень лінійної функції та побудуйте її графік:
|
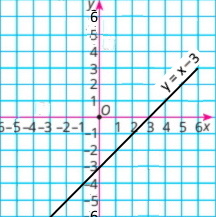
1) у = х – 3;
|
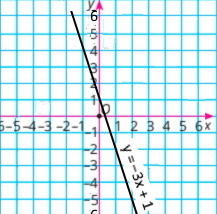
2) у = –3х + 1.
|
||||||||||||
 |
 |
Завдання 1051 Гафіки лінійної функції
|
1) у = х + 2
|
2) у = –3х + 4
|
3) у = 0,5х – 3
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
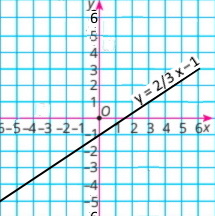
4) y = 2/3x – 1
|
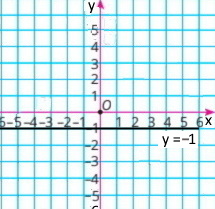
5) y = –1
|
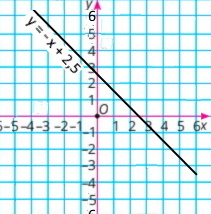
6) y = –х + 2,5
|
||||||||||||||||||
|
|
|
|
Завдання 1052
|
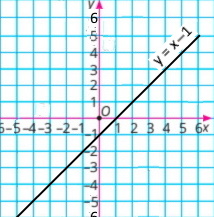
1) y = х – 1
|
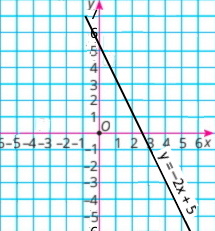
2) y = –2х + 5
|
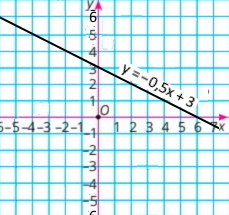
3) y = –0,5х + 3
|
||||||||||||||||||
|
|
|
|
||||||||||||||||||
|
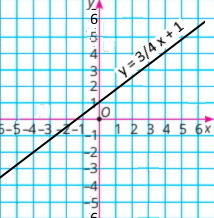
4) y = 3/4 х + 1
|
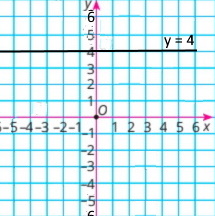
5) y = 4
|
6) y = х – 1,5
|
||||||||||||||||||
|
|
|
|
Завдання 1053
Мотоциклістка рухається зі швидкістю 65 км/год. Задайте формулою залежність відстані s (у кілометрах) від часу t (у годинах), за який вона подолає цю відстань. Чи є ця залежність прямою пропорційністю? Залежність, задана формулою s = 65t, є прямою пропорційністю.
Завдання 1054
1) Залежність довжини кола від його радіуса: — C = 2πr — є прямою пропорційністю
2) залежність площі круга від радіуса: S = πr²
Завдання 1055
Запишіть формули будь–яких двох лінійних функцій, графіки яких проходять через точку Р(1; –5): у = х – 6 i у = 2х – 7.
Завдання 1056
Серед даних функцій знайдіть ті, графіки яких проходять через точку (1; –4):
1) y = 4х; Ні, бо –4 = 4 • 1; –4 = 4 — неправильна рівність;
2) y = 2х – 2; Ні, бо –4 = 2 • 1 – 2; – 4 = 0 — неправильна рівність;
3) y = 1; Ні, бо –4 = 1 — неправильна рівність;
4) y = –4; Так, бо –4 = –4 — правильна рівність;
5) y = –4х; Так, бо –4 = –4 • 1; –4 = –4 — правильна рівність;
6) y = 1/4x – 1/4. Ні, бо –4 = 1/4 • 1 – 1/4; –4 = 0 — неправильна рівність.
Завдання 1057
Не виконуючи побудови графіка функції y = 1,8х – 7, з'ясуйте, чи проходить цей графік через точку:
1) А(0; 7); Ні, бо 7 = 1,8 • 0 – 7; 7 = –7 — неправильна рівність;
2) B(–5; –16); Так, бо –16 = 1,8 • (–5) – 7; –16 = –16 — правильна рівність;
3) С(5; –2); Ні, бо –2 = 1,8 • 5 – 7; –2 = 2 — неправильна рівність;
4) D(10; 11). Так, бо 11 = 1,8 • 10 – 7; 11 = 11 — правильна рівність.
Завдання 1058
Не будуючи графік функції y = –3х + 7, з'ясуйте, чи належить йому точка:
1) А(1; –4); Ні, бо –4 = –3 • 1 + 7; –4 = 4 — неправильна рівність;
2) B(0; 7); Так, бо 7 = –3 • 0 + 7; 7 = 7 — правильна рівність;
3) С(–1; 10); Так, бо 10 = –3 • (–1) + 7; 10 = 10 — правильна рівність;
4) D(10; –37). Ні, бо –37 = –3 • 10 + 7; –37 = –23 — неправильна рівність.
Завдання 1059 Нулі функції
1) y = 2x – 6; у = 0, якщо 2x – 6 = 0; 2х = 6; х = 3
2) у = –1/2x + 8; y = 0, якщо –1/2x + 8 = 0; –1/2х = –8; х = 16
3) у = 7х; у = 0, якщо 7х = 0; х = 0
4) у = –5х; у = 0, якщо –5х = 0; х = 0
Завдання 1060
1) у = 4х + 12; у = 0, якщо 4х + 12 = 0; 4х = –12; х = –3
2) у = –8х; у = 0, якщо –8х = 0; х = 0
Завдання 1061 Графіки прямої пропорційності
|
1) y = х
|
2) y = –2,5х
|
||||||||||||
|
|
|
||||||||||||
|
3) y = –х
|
4) y = 1/2 х
|
||||||||||||
|
|
|
Завдання 1062
|
1) y = 1,5х
|
2) y = –2х
|
||||||||||||
|
|
|
Завдання 1063
Графік функції y = 5 – 2,5x.
|
x |
0 |
2 |
|
y |
5 |
0 |
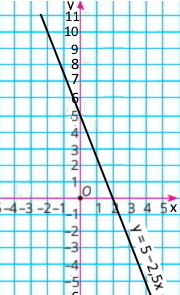
За графіком знайдіть:
1) якщо x = 0, тоді y = 5; якщо x = 2, тоді y = 0;
2) якщо y = –5, тоді x = 4; якщо y = 0, тоді x = 2; якщо y = 10, тоді x = –2;
3) якщо y = 0, тоді x = 2;
4) функція набуває додатних значень, якщо x < 2;
5) функція набуває від'ємних значень, якщо x > 2;
6) точки перетину графіка з осями координат: (2;0) і (0;5).
Завдання 1064
Графік функції y = 1,5x – 3
|
x |
0 |
2 |
|
y |
–3 |
0 |
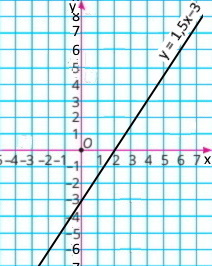
За графіком знайдіть:
1) якщо x = –2, тоді y = –6; якщо x = 0, тоді y = –3; якщо x = 4, тоді y = 3;
2) якщо y = –3, тоді x = 0; якщо y = 0, тоді x = 2; якщо y = 6, тоді x = 6;
3) якщо y = 0, тоді x = 2;
4) функція набуває додатних значень, якщо x > 2;
5) функція набуває від'ємних значень, якщо x < 2;
6) точки перетину графіка з осями координат: (2; 0) і (0; –3).
Завдання 1065
Графік функції y = kx – 2 проходить через точку (6; –11). Знайдіть значення k.
–11 = k • 6 – 2
6k = –11 + 2
6k = –9
k = –1,5
Завдання 1066
Знайдіть значення l, якщо графік функції y = –1/5x + l проходить через точку М(10;–5).
–5 = –1/5 • 10 + l
–5 = –2 + l
l = –3
Завдання 1067
Не виконуючи побудови, знайдіть координати точок перетину графіка функції з осями координат:
1) Координати точки перетину графіка функції у = 1,5х – 20:
а) з віссю абсцис — (13 1/3;0), бо у = 0, якщо 1,5x – 20 = 0; 1,5x = 20; х = 13 1/3;
б) з віссю ординат — (0;–20), бо х = 0, якщо у = 1,5 • 0 – 20; у = –20;
2) координати точки перетину графіка функції у = 5 – x/4:
а) з віссю абсцис — (20;0), бо у = 0, якщо 5 – x/4 = 0; –x/4 = –5; х = 20;
б) з віссю ординат — (0;5), бо х = 0, якщо у = 5 – 0/4; y = 5.
Завдання 1068
1) Координати точки перетину графіка функції у = 0,2х – 40:
а) з віссю абсцис — (200;0), бо у = 0, якщо 0,2x – 40 = 0; 0,2х = 40; x = 200;
б) з віссю ординат — (0;–40), бо х = 0, якщо у = 0,2 • 0 – 40; у = –40;
2) координати точки перетину графіка функції у = 18 – 1/3x:
а) з віссю абсцис — (54; 0), бо у = 0, якщо 18 – 1/3х = 0; –1/3х = –18; х = 54;
б) з віссю ординат — (0; 18), бо x = 0, якщо у = 18 – 1/34 • 0; y = 18.
Завдання 1069
Точка А(0,7; 70) належить графіку прямої пропорційності. Задайте цю функцію формулою.
у = kх
70 = k • 0,7
k = 70 : 0,7
k = 100. Формула набуває вигляду y = 100x.
Завдання 1070
Задайте формулою пряму пропорційність, якщо її графік проходить через В(–2; 18).
у = kх
18 = k • (–2);
k = – 9. Формула набуває вигляду у = –9х.
Завдання 1071 Графіки функції:
|
1) у = 1/2(6 – x) = –0,5х + 3
|
2) у = (x – 5)/5 = 0,2х – 1
|
||||||||||||
|
|
|
Завдання 1072 Графіки функції:
|
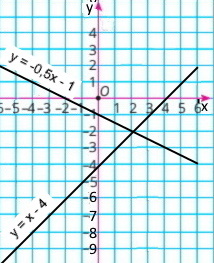
1) y = –0,5x – 1 і y = x – 4 |
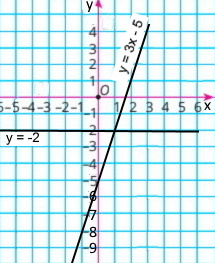
2) y = –2 і y = 3x – 5 |
|
Графіки перетинаються в точці з координатами (2;–2) |
Графіки перетинаються в точці з координатами (1;–2) |
Завдання 1073
Графіки функцій: y = 1,5x – 4 і y = 2
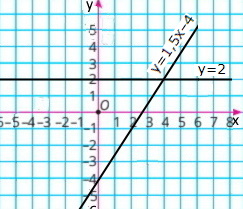
Графіки перетинаються в точці з координатами (4; 2)
Завдання 1074
Усі точки графіка функції y = kx + l мають одну й ту саму ординату, яка дорівнює 5. Знайдіть k і l.
За умовою у = 5 при будь-якому х, тому функція задається формулою 5 = 0x + l.
Отже, l = 5; k = 0.
Завдання 1075
Графік функції y = kx + l паралельний осі абсцис і проходить через точку М(0; –5). Знайдіть k і l.
За умовою графік паралельний осі абсцис, тому всі точки графіка мають одну й ту саму
ординату при будь–якому х і фукнція задається формулою у = 0x + l; у = l. Якщо
графік функції у = l ще проходить через точку M(0;–5), тоді у = –5. Отже, k = 0; l = –5.
Завдання 1076
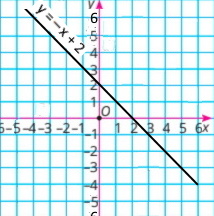
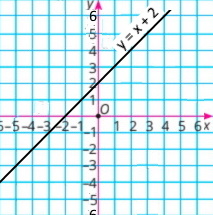
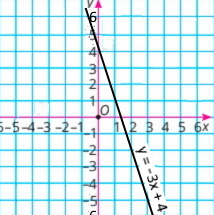
у = Зх відповідає графіку III, у = –Зх — графіку І, а у = х + 3 — графіку II
Завдання 1077
Функцію y = 2x + 1 задано для –3 ≤ x ≤ 4. Знайдіть область значень цієї функції.
Якщо х = –3, тоді y = 2 • (–3) + 1 = –5; Якщо х = 4, тоді y = 2 • 4 + 1 = 9.
Областю значень цієї функції є такі числа y, що: –5 ≤ y ≤ 9
Завдання 1078
Не будуючи графіка функції y = 4x – 6, знайдіть таку його точку, у якої:
1) Якщо абсциса точки графіка дорівнює ординаті;
Підставимо у = х в графік функції у = 4х – 6, отримаємо:
х = 4х – 6; –3х = –6; х = 2 Отже, шукана точка (2;2)
2) якщо абсциса і ордината точки графіка — протилежні числа;
Підставимо у = –х в графік функції у = 4х – 6, отримаємо:
–х = 4х – 6; –5х = –6; х = 1,2 Отже, шукана точка (1,2;–1,2)
3) якщо абсциса точки графіка у два рази менша за ординату.
Підставимо у = 2х в графік функції у = 4х – 6, отримаємо:
2х = 4х – 6; –2х = –6; х = 3; у = 2 • 3 = 6. Отже, шукана точка (3;6)
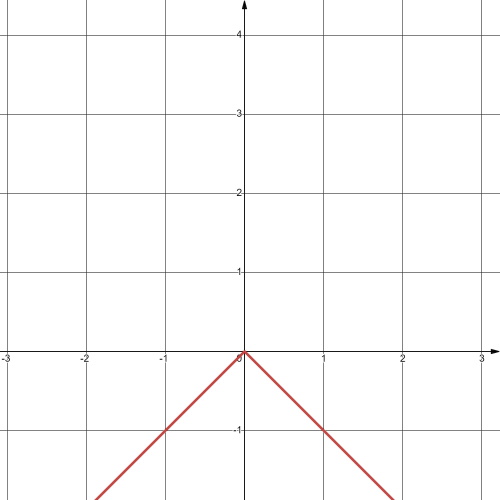
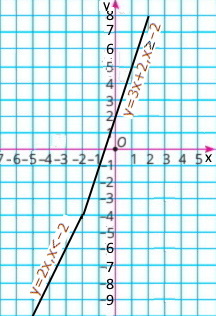
Завдання 1079 Побудуйте графік функції
|
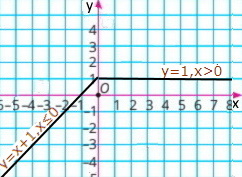
1) y = {х + 1, якщо х ≤ 0, 1, якщо х > 0; |
2) у = {2х, якщо х < –2, 3х + 2, якщо х ≥ –2. |
|
|
 |
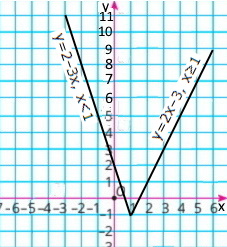
Завдання 1080 Побудуйте графік функції
у = {2 – Зх, якщо х < 1,
2х –3 , якщо х ≥ 1.
Завдання 1081
|
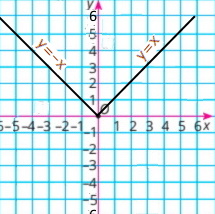
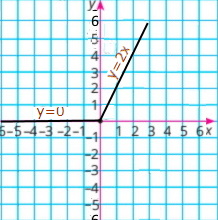
1) y = |x| |
2) y = |x| + x |
|
|
 |
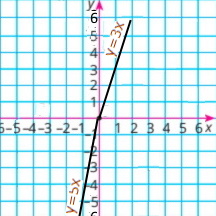
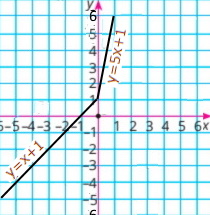
| 3) y = 4x – |x| | 4) y = |2x| + 3x + 1 |
 |
 |
Завдання 1082
|
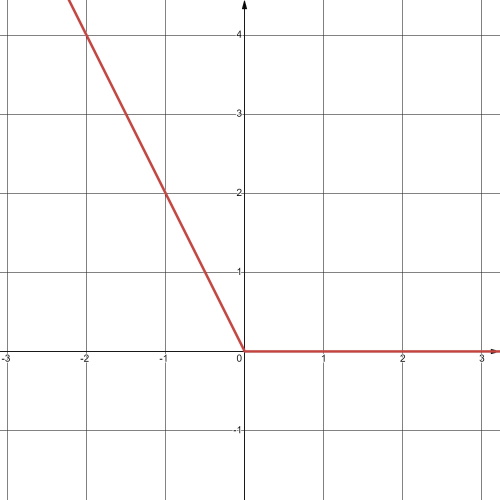
1) y = –|x| |
2) y = |x| – x |
|
|
 |
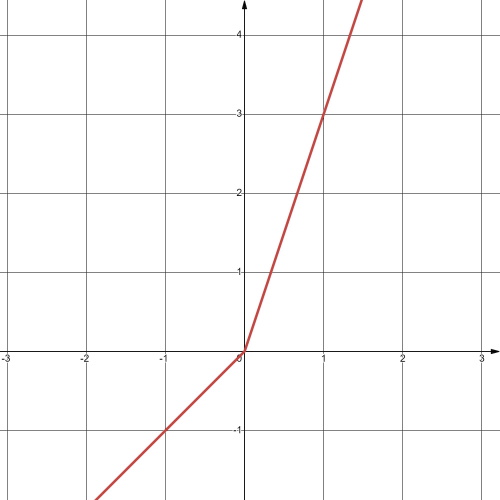
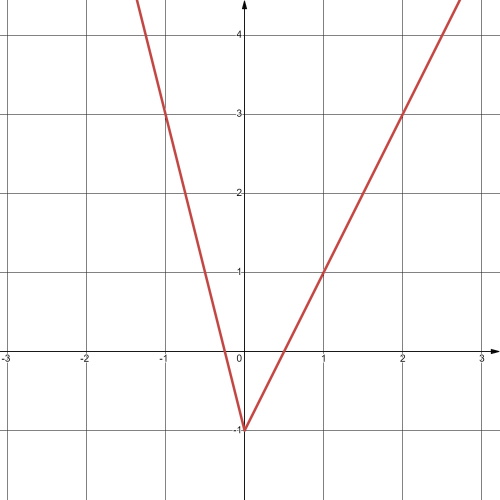
| 3) y = 2x + |x| | 4) y = |3x| – x – 1 |
 |
 |
Завдання 1083 Рівняння
|
1) (2x + 5)² – (2х – 3)² = 16 4х² + 20х + 25 – (4х² – 12х + 9)= 16 4х² + 20х + 25 – 4х² + 12х – 9 = 16 4х² + 20х – 4х² + 12х = 16 – 25 + 9 32х = 0 х = 0 |
2) (7х + 1)² – (49х – 2)(х – 1) = –66 49x² + 14х + 1 – (49х² – 49х – 2х + 2) = –66 49х² + 14х + 1 – 49x² + 49х + 2х – 2 = –66 49х²+ 14х – 49х² + 49х + 2х = –66 – 1 + 2 65х = –65 х = –1 |
Завдання 1084 Спрощення виразів
1) (5m – 2)(5m + 2) – m(10m – 1) + (m – 1/2)² = 25m² – 4 – 10m² + m + m² – m + 1/4 =
= 16m² – 3 3/4
2) (a + 4y)² – (a – 2y)(a + 2y) – y(4a – 5y) = a² + 8ay + 16у² – a² + 4y² – 4ay + 5y² =
= 25y² + 4ay
Завдання 1085
На столі лежить 73 зошити, а в коробці – 17 зошитів. Скільки зошитів потрібно перекласти зі стола в коробку, щоб у коробці їх стало вдвічі менше, ніж на столі?
Розв'язання
Нехай треба перекласти зі стола у коробку x зошитів, тоді на столі залишиться (73 – х) зошитів, а в коробці стане (17 + х) зошитів. Складаємо рівняння:
73 – х = 2 • (17 + х)
73 – х = 34 + 2х
–х – 2х = 34 – 73
–Зх = –39
х = 13 (з.) – потрібно перекласти зі стола в коробку.
Відповідь: 13 зошитів.
Завдання 1086 Квадрат двочлена
1) не можливо;
2) 1/9x² – 2/15xy + 1/25y² = (1/3x – 1/5y)²;
3) не можливо;
4) –36ab + 9a² + 36b² = 9а² – З6аb + 36b² = (3а – 6b)².
Завдання 1087
Вкладниця відкрила в банку «Щасливий» депозит на 20 000 грн. Через рік їй було нараховано 3200 грн відсоткових коштів.
1) Який відсоток річних нараховує банк?
20 000 грн — 100%
3200 грн — х %
20000/3200 = 100/х; 20000х = 320000; х = 16% – річних нараховує банк.
Відповідь: 16%.
2) Після сплати податку на доходи фізичних осіб вкладниця отримала відсоткові кошти в сумі 2624 грн. Скільки відсотків становить податок на доходи фізичних осіб?
3200 – 2624 = 576 (грн) – податок на доходи фізичних осіб.
3200 грн — 100%
576 грн — х%
3200/576 = 100/х; 3200х = 57600; х = 18% – становить податок на доходи фізичних осіб.
Відповідь: 18%.
Завдання 1088
Давня аравійська задача. В Аравії помер старий. Усе своє майно, 17 верблюдів, він заповів своїм синам, причому старший мав одержати половину, середній – третину, а найменший – дев'яту частину цього майна. Після смерті батька сини не змогли виконати заповіт, бо 17 не ділилося без остачі ані на 2, ані на 3, ані на 9. Довго сперечалися брати, аж тут на верблюді під'їхав до них мудрець. Довідався про суперечку і дав братам слушну пораду, яка і допомогла розділити майно відповідно до батькового заповіту. Що саме порадив мудрець? Мудрець в обчисленнях додав свого верблюда, а в дійсності залишив його в себе.
1) 1 + 17 = 18 (в.) – стало верблюдів;
2) 18 • 1/2 = 9 (в.) – віддав половину старшому синові:
3) 18 • 1/3 = 6 (в.) – віддав третину середньому синові;
4) 18 • 1/9 = 2 (в.) – віддав дев'яту частину молодшому синові;
5) 9 + 6 + 2 = 17 (в.) – всього роздав верблюдів.
Відповідь: мудрець роздав 17 верблюдів, а поділив майно, додавши в обчисленнях свого верблюда.