Завдання 1102 Рівняння з двома змінними
|
1) x² – 3xy = 5 Так 3) 3x + 2y = 5 Так 5) x + 2x² = y – 3y² Так |
2) 4x² – 5x – 1 = 0 4) x + y + z = 8 6) x/y + y/z + z/x = 3 |
Завдання 1103 Лінійні рівняння з двома змінними
|
1) 4x – 5y = 9 Так 4) (x + 2)/(y – 1) = 7 |
2) 3x² – 4y = 5 5) 0x + 3y = 12 Так |
3) 2x + 11y = 0 Так 6) 13x + 2y² = 3 |
Завдання 1104
Укажіть рівняння з двома змінними. Які з них є лінійними:
|
1) 3x – 2y = 5 Лінійне 4) 4x – 0y = 8 Лінійне |
2) 2x² – 3y² = 1 5) xyz = 12 |
3) (x – 2)(y + 1) = 5 6) 1/7x + 1/8y=1/9 Лінійне |
Завдання 1105
Чи є пара чисел розв'язком рівняння x – y = 0:
1) Пара чисел (4; 4) є розв’язком рівняння, бо 4 – 4 = 0; 0 = 0;
2) пара чисел (–1; 1) не є розв’язком рівняння, бо –1 – 1 = –2; –2 ≠ 0;
3) пара чисел (0; 0) є розв’язком рівняння, бо 0 – 0 = 0; 0 = 0.
Завдання 1106
Чи є пара чисел x = 2; y = 3 розв'язком рівняння x + y = 5? Знайдіть ще три розв'язки цього рівняння.
Пара чисел (2; 3) є розв’язком рівняння, бо 2 + 3 = 5; 5 = 5;
Пара чисел (1;4) є розв'язком рівняння, бо 1 + 4 = 5; 5 = 5;
Пара чисел (0;5) є розв'язком рівняння, бо 0 + 5 = 5; 5 = 5;
Пара чисел (3;2) є розв'язком рівняння, бо 3 + 2 = 5; 5 = 5.
Завдання 1107
Які з пар чисел (10; 1), (1; 10), (7; 2), (7; –2), (9; 0) є розв'язками рівняння x – y = 9?
Пара чисел (10; 1) є розв’язком рівняння, бо 10 – 1 = 9; 9 = 9;
Пара чисел (1; 10) не є розв’язком рівняння, бо 1 – 10 = –9; –9 ≠ 9;
Пара чисел (7; 2) не є розв’язком рівняння, бо 7 – 2 = 5; 5 ≠ 9;
Пара чисел (7; –2) є розв’язком рівняння, бо 7 – (–2) = 7 + 2 = 9; 9 = 9;
Пара чисел (9; 0) є розв’язком рівняння, бо 9 – 0 = 9; 9 = 9.
Завдання 1108
Які з пар чисел (2; 1), (2; –1), (0; 5), (1; 3), (–1; 5) є розв'язками рівняння 2x + y = 5?
Пара чисел (2; 1) є розв’язком рівняння, бо 2 • 2 + 1 = 5; 5 = 5;
Пара чисел (2; –1) не є розв’язком рівняння, бо 2 • 2 – 1 = 3; 3 ≠ 5;
Пара чисел (0; 5) є розв’язком рівняння, бо 2 • 0 + 5 = 5; 5 = 5;
Пара чисел (1; 3) є розв’язком рівняння, бо 2 • 1 + 3 = 5; 5 = 5;
Пара чисел (–1; 5) не є розв’язком рівняння, бо 2 • (–1) + 5 = 3; 3 ≠ 5.
Завдання 1109
Розв'язком яких рівнянь є пара чисел (–1; 3):
1) Не є розв’язком 2х – 17y = 53, бо: 2 • (–1) – 17 • 3 = –2 – 51 = – 53; – 53 ≠ 53;
2) Є розв’язком Зх² + у² = 12, бо: 3 • (–1)² + З² = 3 + 9 = 12; 12 = 12;
3) Є розв’язком (х – 3)(у + 2) = –20; бо: ((–1) – 3)(3 + 2) = –4 • 5 = –20; –20 = –20;
4) Не є розв’язком 0x + 4у = –12, бо: 0 • (–1) + 4 • 3 = 12; 12 ≠ –12;
5) Є розв’язком 0x + 0у = 0, бо: 0 • (–1) + 0 • 3 = 0; 0 = 0;
6) Є розв’язком х² + 1 = у² – 7, бо: (–1)² + 1 = З² – 7 = 2; 2 = 2.
Завдання 1110
Розв'язком яких рівнянь є пара чисел x = 2; y = –1:
1) Є розв’язком 3х + у = 5, бо: 3 • 2 – 1 = 5; 5 = 5;
2) Не є розв’язком х² + у² = 3, бо: 2² + (–1)² = 5; 5 ≠ 3;
3) Є розв’язком 2х + 0y = 4, бо: 2 • 2 + 0 • (–1) = 4; 4 = 4;
4) Не є розв’язком х(у + 3) = 14, бо: 2 • (–1 + 3) = 2 • 2 = 4; 4 ≠ 14;
5) Не є розв’язком 0x + 0y = 7, бо: 0 • 2 + 0 • (–1) = 0; 0 ≠ 7;
6) Є розв’язком 1/2x + у = 0, бо: 1/2 • 2 – 1 = 0 ; 0 = 0.
Завдання 1111
Знайдіть три будь–яких розв'язки рівняння:
1) х + у = –3;
Якщо х = –1 , то –1 + у = –3; у = –2
Якщо х = 0, то 0 + у = –3; у = –3
Якщо x = 1, то 1 + у = –3; у = –4
Отже, пари чисел (–1;–2), (0;–3), (1;–4) є розв’язками рівняння.
2) х – 2у = 5.
Якщо х = –5, то –5 – 2у = 5; 2у = –10; у = –5
Якщо х = 0, то 0 – 2у = 5; 2у = –5; у = –2,5
Якщо х = 5, то 5 – 2у = 5; 2у = = 0; у = 0
Отже, пари чисел (–5;–5), (0;–2,5), (5;0) є розв’язками рівняння.
Завдання 1112
Знайдіть три будь–яких розв'язки рівняння:
1) х – у = 2;
Якщо х = –3, то – 3 – у = 2; у = –5
Якщо х = 0, то 0 – у = 2; у = –2
Якщо х = 3, то 3 – у = 2; у = 1
Отже, пари чисел (–3;–5), (0;–2), (3;1) є розв’язками рівняння.
2) х + Зу = 0.
Якщо х = –3, то –3 + 3у = 0; Зу = 3; у = 1
Якщо х = 0, то 0 + Зу = 0; Зу = 0; у = 0
Якщо х = 3, то 3 + 3у = 0; Зу = –3; у = –1
Отже, пари чисел (–3;1), (0;0), (3;–1) є розв’язками рівняння.
Завдання 1113
Складіть лінійне рівняння з двома змінними, розв'язком якого є пара чисел x = 3; y = –2.
х + 2у = –1, бо 3 + 2 • (–2) = –1; –1 = –1
Завдання 1114
Складіть лінійне рівняння з двома змінними, розв'язком якого є пара чисел (–2;0).
5x + у = –10, бо 5 • (–2) + 0 = –10; –10 = –10
Завдання 1115
Виразіть з рівняння 5x + y = 7 змінну у через змінну х. у = 7 – 5х
Завдання 1116
Виразіть з рівняння x – 3y = 9 змінну х через змінну у. х = 9 + Зу
Завдання 1117
З лінійного рівняння 3x – 2y = 12 виразіть:
|
1) змінну у через змінну х; –2у = 12 – 3х у = –6 + 1,5х |
2) змінну х через змінну у. 3х = 12 + 2у х = 4 + 2/3у |
Завдання 1118
Виразивши в рівнянні змінну у через змінну х, знайдіть два будь–яких розв'язки рівняння:
1) x + y = 29; у = 29 – х
Якщо х = 0, то у = 29 – 0 = 29. Якщо х = 19, то у = 29 – 19 = 10
Отже, пари чисел (0;29), (19;10) є розв’язками рівняння.
2) 5x + y = 7; у = 7 – 5х
Якщо х = 0, то y = 7 – 5 • 0 = 7. Якщо х = 3, то у = 7 – 5 • 3 = –8
Отже, пари чисел (0;7), (3;–8) є розв’язками рівняння.
3) 3x – 2y = 15; 2y = 3x – 15; у = 1,5x – 7,5
Якщо х = 0, то y = 1,5 • 0 – 7,5 = –7,5. Якщо х = 4, то у = 1,5 • 4 – 7,5 = –1,5
Отже, пари чисел (0;–7,5), (4;–1,5) є розв’язками рівняння.
4) 6y – x = 5. 6y = 5 + x; у = (5 + x)/6; у = 5/6 + x/6;
Якщо х = 1, то y = 5/6 + 1/6 = 6/6 = 1. Якщо х = 7, то у = 5/6 + 7/6 = 12/6 = 2
Отже, пари чисел (1;1), (7;2) є розв’язками рівняння.
Завдання 1119
Виразивши в рівнянні змінну у через змінну х або змінну х через змінну у, знайдіть три будь–яких розв'язки рівняння:
1) х – 2y = –8; х = –8 + 2у.
Якщо у = –1, то х = –8 + 2 • (–1) = –10
Якщо у = 0, то х = –8 + 2 • 0 = –8
Якщо у = 4, то х = –8 + 2 • 4 = 0
Отже, пари чисел (–10;–1), (–8;0), (0;4) є розв’язками рівняння.
2) 7x – у = 9; –у = 9 – 7х; у = 7x – 9
Якщо х = –2, то у = 7 • (–2) – 9 = –23
Якщо х = 0, то у = 7 • 0 – 9 = –9
Якщо х = 2, то 7 • 2 – 9 = 5
Отже, пари чисел (–2;–23), (0;–9), (2;5) є розв’язками рівняння.
3) 3х + 2у = 6; 2y = 6 – 3х; у = 3 – 1,5х.
Якщо х = –2, то у = 3 – 1,5 • (–2) = 6
Якщо х = 0, то y = 3 – 1,5 • 0 = 3
Якщо х = 2, то у = 3 – 1,5 • 2 = 0
Отже, пари чисел (–2;6), (0;3), (2;0) є розв’язками рівняння.
4) 5x – 7y = 12; 5х = 12 + 7y; х = 1,4у + 2,4.
Якщо у = –5, то х = 1,4 • (–5) + 2,4 = 4,6
Якщо у = 0, то х = 1,4 • 0 + 2,4 = 2,4
Якщо у = 5, то х = 1,4 • 5 + 2,4 = 9,4
Отже, пари чисел (4,6;–5), (2,4;0), (9,4;5) є розв’язками рівняння.
Завдання 1120
Пара чисел (–5;р) є розв'язком рівняння 2x – y = –13. Знайдіть р.
Підставимо х = –5 і у = р у рівняння:
2 • (–5) – р = –13
–10 – р = – 13
–р = –13 + 10
р = 3
Завдання 1121
Пара чисел (n;–1) є розв'язком рівняння 3x + 5y = 4. Знайдіть n.
Підставимо х = n і у = –1 у рівняння:
3n + 5 • (–1) = 4
3n = 9
n = 3
Завдання 1122
Знайдіть m, якщо пара чисел (–1;–3) є розв'язком рівняння:
|
1) 8x + 9y = m; Якщо х = –1 і у = –3, тоді 8 • (–1) + 9 • (–3) = m –8 – 27 = m m = –35 |
2) mx – 2y = –9. Якщо х = –1 і у = –3, тоді m • (–1) – 2 • (–3) = –9 –m + 6 = –9 –m = –15 m = 15 |
Завдання 1123
Для якого значення d пара чисел (2;–1) є розв'язком рівняння:
|
1) 7x – 5y = d; Якщо х = 2 і у = –1, тоді 7 • 2 – 5 • (–1) = d 14 + 5 =d d = 19 |
2) 3x + dy = 8? Якщо х = 2 і у = –1, тоді З • 2 + d • (–1) = 8 6 – d = 8 d = –2 |
Завдання 1124
Знайдіть два деяких розв'язки рівняння 2(x – y) = 3(x + y) + 4.
2х – 2у = 3х + 3у + 4
2х – 2у – 3х – 3у = 4
–х – 5у = 4
х = –5y – 4
Якщо у = 0, то х = –5 • 0 – 4 = –4. Якщо y = 1, то х = –5 • 1 – 4 = = –9
Отже, пари чисел (–4;0), (–9;1) є розв’язками рівняння.
Завдання 1125
Серед розв'язків рівняння x + 3y = 20 знайдіть пару рівних між собою чисел.
Якщо х = у, то х + 3х = 20; 4х = 20; х = 5
Отже, розв’язком рівняння х + 3у = 20 є, пара чисел (5;5).
Завдання 1126
Знайдіть р, якщо:
1) пара (р; р) є розв'язком рівняння 4x – 9y = –10;
х = р і у = р підставляємо в рівняння:
4р – 9р = –10
–5р = –10
р = 2
2) пара (р; –р) є розв'язком рівняння 17x + 12y = 105.
х = р і у = –р підставляємо в рівняння:
17p – 12p = 105
5p = 105
p = 21
Завдання 1127
Знайдіть усі пари натуральних чисел, які є розв'язками рівняння:
1) 2х + у = –7;
Якщо х і у — натуральні числа, то сума подвоєного числа х і числа у не може дорівнювати від’ємному числу. Отже, таких пар натуральних чисел немає.
2) Зх + 2у = 5;
Якщо х і у — натуральні числа, то х може набирати лише значення 1.
Якщо х = 1, то 3 • 1 + 2у = 5; 2у = 2; у = 1
Розв’язком рівняння є пара чисел (1;1).
3) х + 7y = 15;
Якщо х і у — натуральні числа, то у може набирати лише значення 1 або 2.
Якщо у = 1, то х + 7 • 1 = 15; х = 8. Якщо у = 2, то х + 7 • 2 = 15; х = 1
Розв’язком рівняння є пари чисел: (8;1) або (1;2).
4) ху = 7.
Якщо х і у — натуральні числа, то у може набирати лише значення 1 або 7.
Якщо у = 1, то x • 1 = 7; х = 7. Якщо у = 7, то х • 7 = 7; х = 1
Розв’язком рівняння є пари чисел: (7;1) або (1;7).
Вправи для повторення
Завдання 1128
Функцію задано формулою у = (2x + 1)/(x – 6). Заповніть у зошиті таблицю, обчисливши відповідні значення функції:
Якщо х = –3, то у = (2 • (–3) + 1)/(–3 – 6) = (–6 + 1)/(–9) = 5/9
Якщо х = –2, то у = (2 •(–2) + 1)/(–2 – 6) = (–4 + 1)/(–8) = 3/8
Якщо х = –1, то у = (2 • (–1) + 1)/(–1 – 6) = (–2 + 1)/(–7) = 1/7
Якщо х = 0, то у = (2 • 0 + 1)/(0 – 6) = 1/(–6) = –1/6
Якщо х = 1, то у = (2 • 1 + 1)/(1 – 6) = 3/(–5) = –3/5
Якщо х = 2, то у = (2 • 2 + 1)/(2 – 6) = 5/(–4) = –5/4
Якщо х = 3, то у = (2 • 3 + 1)/(3 – 6) = 7/(–3) = –7/3
Якщо х = 4, то у = (2 • 4 + 1)/(4 – 6) = 9/(–2) = –9/2
|
x |
–3 |
–2 |
–1 |
0 |
1 |
2 |
3 |
4 |
|
y |
5/9 |
3/8 |
1/7 |
–1/6 |
–3/5 |
–5/4 |
–7/3 |
–9/2 |
Завдання 1129
Спростіть вираз і знайдіть його значення:
1) (х – 10)² – х(х + 80) = х² – 20х + 100 – х² – 80x = 100 – 100х
Якщо x = –0,83, тоді 100 – 100x = 100 – 100 • (–0,83) = 100 + 83 = 183
2) (5m + З)² – (5m – З)² = (5m + 3 – 5m + 3)(5m + 3 + 5m – 3) = 6 • 10m = 60m
Якщо m = –17/60, то 60m = 60 • (–17/60) = –17
Завдання 1130
Відомо, що a + b = –1, ab = –6. Знайдіть значення виразів:
1) a²b + ba² = ab(a + b)
Якщо а + b = –1, ab = –6, тоді ab(a + b) = –6 • (–1) = 6
2) а² + b² = a² + b² + 2ab – 2ab = (а + b)² – 2ab
Якщо а + b = –1, ab = –6, тоді (а + b)² – 2ab = (–1)² – 2 • (–6) = 13
3) (а – b)² = а² – 2ab + b² + 2ab – 2ab = а² + 2ab + b² – 2ab – 2ab = (а + b)² – 4ab
Якщо а + b = – 1, ab = –6, тоді (а + b)² – 4ab = (–1)² – 4 • (–6) = 25
4) а3 + b3 = (а + b)(a² – ab + b²) = (а + b)(a² + 2ab + b² – 3ab) = (а + b)((а + b)² – Заb)
Якщо а + b = –1, ab = –6 , тоді (а + b)((a + b)² – 3ab) = –1 • ((–1)² – 3 • (–6)) =
= –1 • ( 1 + 18) = –19
Завдання 1131
Роздрібна ціна підручника для 7 класу становить 360 грн, що на 20% вище за оптову ціну. Скільки коштуватимуть 28 таких підручників, придбаних для 7 класу, за оптовою ціною?
Розв'язання
360 • 0,8 = 288 (грн) – ціна підручника за оптовою ціною;
288 • 28 = 8064 (грн) – коштуватимуть всі підручники за оптовою ціною.
Відповідь: 8064 грн.
Завдання 1132 Графіки лінійної функції
|
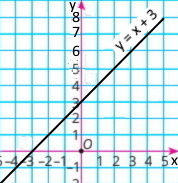
1) 1) y = x + 3
|
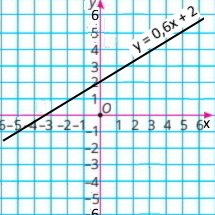
3) y = 0,6x + 2
|
||||||||||||
|
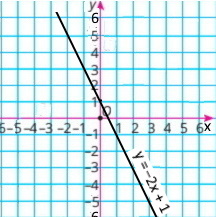
2) y = –2x + 1
|
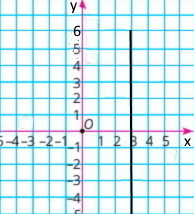
2) 4) y = –2
|
Завдання 1133
Дано два трицифрових числа, сума яких ділиться на 37. Ці числа записали в рядок одне за одним. Доведіть, що отримане в такий спосіб шестицифрове число також ділиться на 37.
Розв'язання
Нехай abc і def — задані числа. За умовою, abc + def ділиться на 37. Записавши ці числа в рядок, одержимо число abcdef = 1000 abc + def = 999 abc + abc + def. Перший доданок ділиться на 37, сума другого й третього ділиться на 37 за умовою, тому і число abcdef ділиться на 37.