Завдання 1. Приклад завдання на знаходження значення виразу (з дужками) з багатоцифровими числами, що передбачає визначення порядку дій.
Знайди значення виразу. Обчислення запиши окремими діями. 149 + (13 028 – 26 265 : 85)
Розв'язання.
149 + (13 028 – 26 265 : 85) = 12868
|
1) _26265 | 85 255 309 76 0 765 765 0 |
2) _13028 309 12719
|
3) +12719 149 12868
|
Завдання 2. Приклади завдань на порівняння чисел і величин.
1) 1 мільйон 24 тисячі 405 □ число, яке складається зі 107 одиниць другого класу і 5 одиниць першого класу
Розв'язання.
1 мільйон 24 тисячі 405 ˃ число, яке складається зі 107 одиниць другого класу і 5 одиниць першого класу.
|
Міркуємо так. Для порівняння чисел запишемо словесне представлення за допомогою цифр. 1 мільйон 24 тисячі 405 = 1 024 405 Число, яке складається зі 107 одиниць другого класу і 5 одиниць першого класу = 107 005 1 024 405 ˃ 107 005 |
2) 726 см 8 мм □ 72 дм 68 мм
Розв'язання.
726 см 8 мм = 72 дм 68 мм
|
Міркуємо так. Якщо кількість цифр у величинах однакова, то порівнюємо величини вимірювання. Інакше для порівняння величин зведемо величини до однакових одиниць вимірювання. Нагадаємо, що 1 см = 10 мм, 1 дм = 10 см = 100 мм Щоб перевести величину від більших одиниць вимірювання до менших, виконуємо дію множення. 726 см 8 мм = 726 см + 8 мм = 726 • 1 см + 8 мм = 726 • 10 мм + 8 мм = 7260 мм + 8 мм = 7268 мм 72 дм 68 мм = 72 дм + 68 мм = 72 • 1 дм + 68 мм = 72 • 100 мм + 68 мм = 7200 мм + 68 мм = 7268 мм 7268 мм = 7268 мм |
Завдання 3. Приклади завдань на перетворення величин.
1) 540 с = □ хв
Розв'язання.
540 с = 9 хв
|
Міркуємо так. Якщо кількість цифр у величинах однакова, то порівнюємо величини вимірювання. Інакше для порівняння величин зведемо величини до однакових одиниць вимірювання. Нагадаємо, що 60 с = 1 хв. Щоб перевести величину від менших одиниць вимірювання до більших, виконуємо дію ділення. 540 с = (540 : 60) хв = 9 хв |
2) 3 ц 10 кг = □ кг
Розв'язання.
3 ц 10 кг = 310 кг
|
Міркуємо так. Якщо кількість цифр у величинах однакова, то порівнюємо величини вимірювання. Інакше для порівняння величин зведемо величини до однакових одиниць вимірювання. Нагадаємо, що 1 ц = 100 кг. Щоб перевести величину від більших одиниць вимірювання до менших, виконуємо дію множення. 3 ц 10 кг = 3 ц + 10 кг = 3 • 1 ц + 10 кг = 3 • 100 кг + 10 кг = 300 кг + 10 кг = 310 кг |
Завдання 4. Приклади завдань на знаходження частини від числа.
1) Запиши число, яке дорівнює 3/4 від 800.
Розв'язання.
800 : 4 • 3 = 200 • 3 = 600 - шукане число.
Відповідь: шукане число 600.
|
Міркуємо так. У дробі 3/4 число 3 - чисельник дробу, 4 - знаменник дробу (у дробі над дробовою рискою знаходиться чисельник дробу, а під дробовою рискою знаходиться знаменник дробу). Щоб знайти дробову частину від числа, треба число поділити на знаменник дробу і помножити на чисельник дробу. Число : Знаменник • Чисельник |
2) Число 600 становить 3/4 від деякого задуманого числа. Знайди задумане число.
Розв'язання.
600 : 3 • 4 = 200 • 4 = 800 - задумане число.
Відповідь: задумане число 800.
|
Міркуємо так. У дробі 3/4 число 3 - чисельник дробу, 4 - знаменник дробу (у дробі над дробовою рискою знаходиться чисельник дробу, а під дробовою рискою знаходиться знаменник дробу). Якщо дане число уже становить дріб від невідомого числа. Щоб знайти невідоме число, треба дане число поділити на чисельник дробу і помножити на знаменник дробу. Число : Чисельник • Знаменник |
Завдання 5. Приклад завдання на застосування геометричного матеріалу.
1) Накресли прямокутник, площа якого 18 см2 , а довжина – 6 см.
|
Міркуємо так. Нагадаємо формулу для знаходження площі прямокутника. S = a • b, де a - довжина прямокутник, b - ширина прямокутника. З формули випливає a = S : b b = S : a |
Розв'язання.
18 : 6 = 3 (см) - ширина прямокутника.
Накреслимо прямокутник довжиною 6 см та шириною 3 см.

1) Накресли прямокутник, периметр якого 18 см , а довжина – 6 см.
|
Міркуємо так. Нагадаємо формулу для знаходження периметра прямокутника. Р = (a + b) • 2 = a • 2 + b • 2, де a - довжина прямокутник, b - ширина прямокутника. З формули випливає a + b = Р : 2 - півпериметр прямокутника дорівнює сумі довжини та ширини прямокутника |
Розв'язання.
18 : 2 = 9 (см) - півпериметр, або сума довжини та ширини прямокутника.
9 - 6 = 3 (см) - ширина прямокутника.
Накреслимо прямокутник довжиною 6 см та шириною 3 см.

Завдання 6. Приклади завдань у тестовій формі закритого типу, які передбачають вибір правильної відповіді із трьох запропонованих варіантів.
1. Познач число, яке є значенням виразу 80 000 + 300 + 9.
|
Міркуємо так. 80 000 + 300 + 9 = 80 309 |
А 8 309
Б 80 309
В 83 009
2. Познач число, яке є найбільшим серед пропонованих.
А 1/8
Б 1/6
В 1/3
|
Міркуємо так. У дробі 1/8 число 1 - чисельник дробу, 8 - знаменник дробу (у дробі над дробовою рискою знаходиться чисельник дробу, а під дробовою рискою знаходиться знаменник дробу). Серед дробів з однаковими чисельниками у більшого дробу менший знаменник (у меншого дробу більший знаменник) |
Познач число, яке є найбільшим серед пропонованих.
А 8/10
Б 6/10
В 3/10
|
Міркуємо так. У дробі 8/10 число 8 - чисельник дробу, 10 - знаменник дробу (у дробі над дробовою рискою знаходиться чисельник дробу, а під дробовою рискою знаходиться знаменник дробу). Серед дробів з однаковими знаменниками в більшого дробу більший чисельник (у меншого дробу менший чисельник) |
3. Познач рядок, у якому числа розміщені у порядку зростання.
А 435 см, 436 м, 437 дм
Б 564 мм, 563 см, 562 дм
В 34 дм, 340 см, 3400 мм
|
Міркуємо так. Якщо кількість цифр у величинах однакова, то порівнюємо величини вимірювання. 435 см < 436 м, але 436 м ˃ 437 дм Якщо кількість цифр у величинах однакова, то порівнюємо величини вимірювання. 564 мм < 563 см < 437 дм - шуканий рядок. |
Нагадаємо, якщо кількість цифр величин різна, для правильності переводимо усі величини до однакових одиниць вимірювання.
Наприклад, зведемо величини останнього рядка до дециметрів (дм). Нагадаємо, що 1 дм = 10 см = 100 мм
Щоб перевести величину від менших одиниць вимірювання до більших, виконуємо дію ділення.
340 см = (340 : 10) дм = 34 дм
3400 мм = (3400 : 100) дм = 34 дм
Маємо, 34 дм = 340 см = 3400 мм
Наприклад, зведемо величини останнього рядка до міліметрів (мм). Нагадаємо, що 1 дм = 10 см = 100 мм, 1 см = 10 мм
Щоб перевести величину від більших одиниць вимірювання до менших, виконуємо дію множення.
340 см = 340 • 1 см = 340 • 10 мм = 3400 мм
34 дм = 34 • 1 дм = 34 • 100 см = 3400 мм
Маємо, 34 дм = 340 см = 3400 мм
Завдання 7. Приклади завдань на встановлення послідовності або відповідності.
1. Пронумеруй величини у порядку зростання.
□ 273 см □ 275 м □ 277 дм
1 273 см 3 275 м 2 277 дм
|
Міркуємо так. Якщо кількість цифр у величинах однакова, то порівнюємо величини вимірювання. 273 см < 277 дм < 275 м |
2. Покажи стрілочками значення кожного виразу.
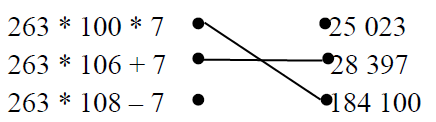
|
Міркуємо так. 263 • 100 • 7 = 1841 • 100 = 184100 х263 7 1841
263 • 106 + 7 = 28397 х 263 106 1578 263 27878
+27878 7 28885
263 • 108 - 7 = 28397
х 263 108 2104 263 28404
_28404 7 28397 |
Завдання 8. Приклад відкритого завдання у тестовій формі, виконання якого передбачає коротку письмову відповідь.
Запиши два числа, які є розв’язками нерівності 600 : b ˂ 10
b 300, 600.
|
Міркуємо так. Розглянемо рівняння 600 : b = 10. Щоб знайти невідомий дільник, треба ділене поділити на частку b = 600 : 10 = 60, тоді можна записати 600 : b = 600 : 60. Розглянемо нерівність 600 : b < 600 : 60. Якщо однакове ділене, то частка менша там, де більший дільник, тому маємо b ˃ 60. |