Завдання 402
|
х 17 3 51 |
_64 | 16 64 4 0 |
18 • 5 + 640 : 160 = 90 + 4 = 94 |
х 18 5 90 |
_640 | 160 640 4 0 |
|
х 27 13 81 27 351 |
_84 | 14 84 6 0 |
180 • 5 – 640 : 320 = 900 – 2 = 898 |
х 180 5 900
|
_640 | 320 640 2 0 |
|
х 45 14 180 45 630 |
_84 | 12 84 7 0 |
32 • 2 + 640 : 10 = 64 + 64 = 128 |
х 32 2 64 |
+ 64 64 128 |
|
х 23 28 184 46 644 |
_84 | 21 84 4 0 |
320 • 2 – 640 : 64 = 640 – 10 = 630 |
х 320 2 640 |
_640 | 64 64 10 0 |
Господар посадив 55 кг картоплі, а зібрав у 12 разів більше. На скільки більше кілограмів картоплі зібрано, ніж посаджено?
|
1) х 55 12 110 55 660 (кг) – зібрав картоплі |
|
2) _660 55 605 (кг) Відповідь: на 605 кг картоплі більше зібрано, ніж посаджено. |
По скільки приблизно картоплин виросло з однієї посадженої картоплини? по 12
Коробка, сірник, мобільний телефон, монітор, книжка, зошит — прямокутник;
кубик — квадрат;
дно кастрюлі, м'яч, тарілка — круг.
P=a + b + c, де a, b, c — сторони трикутника.
|
х |
21 |
24 |
28 |
32 |
|
11 |
231 |
234 |
308 |
352 |
|
18 |
378 |
432 |
504 |
896 576 |
|
25 |
525 |
600 |
700 |
800 |
Побудуй квадрат зі стороною 1 дм.
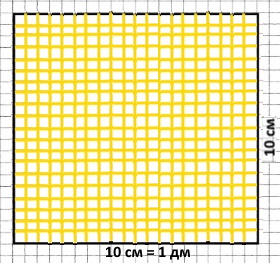
На скільки квадратиків зі стороною 1 см можна його поділити? На 100 квадратиків.
10 • 10 = 100 (см2)
Один дюйм — це приблизно 2 см і 5 мм
Обчисли довжину (в сантиметрах і міліметрах) діагоналей:
|
а) екрана мобільного телефона (5 дюймів); х 25 5 125 (мм) = 12 см 5 мм |
|
б) екрана монітора комп’ютера (17 дюймів); х 25 17 175 25 425 (мм) = 42 см 5 мм |
|
в) екрана телевізора (32 дюйми). х 25 32 50 75 800 (мм) = 80 см |
Дюйм з нім. Daumen — великий палець.
|
х 11 11 11 11 121 |
х 14 14 56 14 196 |
х 17 17 119 17 289 |
|
х 12 12 24 12 144 |
х 15 15 75 15 225 |
х 18 18 144 18 324 |
|
х 13 13 39 13 169 |
х 16 16 96 16 256 |
х 19 19 171 19 361 |
Завдання 411
|
1) х 26 12 52 26 312 (см) – довжина прямокутника |
|
2) (312 + 26) • 2 = 338 • 2 = (300 + 30 + 8) • 2 = 600 + 60 + 16 = 676 (см) Відповідь: периместр цього прямокутника дорівнює 676 сантиметрів. |
Завдання 412