ГДЗ (відповіді) самостійна робота 9 лінійні та стовпчасті діаграми, кут, трикутник Істер

Інші завдання дивись тут ...

Самостійна робота №9

Лінійні та стовпчасті діаграми, кут, трикутник

Варіант 1

Завдання 1 За стовпчастою діаграмою, визнач кількість відмінників у 5–Б класі.

^{5–А — 2 в.}

^{5–Б — 4 в.}

^{5– В — 3 в.}

^{5–Г — 5 в.}

А 2 Б З В 4 Г 5

Завдання 2 Знайди градусну міру кута COD.

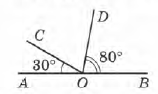
∠AOB = 180° = ∠AOC + ∠COD + ∠BOD

∠COD = ∠AOB – ∠AOC – ∠BOD

∠COD = 180° – 30° – 80° = 70°

Відповідь: ∠COD = = 70°

Завдання 3 Периметр рівнобедреного трикутника дорівнює 40 см, а довжина основи — с см. Склади вираз для обчислення довжини бічної сторони трикутника. Знайди значення цього виразу, якщо с = 18.

^{Короткий запис}

^{Бічні сторони — 2 сторони по ? см}

^{Основа — с см}

^{Р — 40 см}

Розв’язання

^{40 – с (см) – сума довжин двох бічних сторін (бічні сторони рівнобедреного трикутника рівні).}

(40 – с) : 2 (см) – довжина бічної сторони рівнобедреного трикутника.

Якщо с = 18, тоді (40 – с) : 2 = (40 – 18) : 2 = 22 : 2 = 11 (см)

Відповідь: 11 см.

Завдання 4 Кут АОВ утричі менший за кут ВОС. Знайди градусну міру кута АОВ, якщо ∠AOC = 120°

∠АОС = ∠АОВ + ∠ВОС

Нехай х(°) – градусна міра кута АОВ, тоді 3х (°) – градусна міра кута ВОС. Складемо рівняння.

х + 3х = 120

4х = 120

х = 120 : 4

х = 30 (°) – градусна міра кута АОВ.

2 спосіб

1) 1 + 3 = 4 (ч.) – частин складає кут АОС.

2) 120 : 4 = 30 (°) – градусна міра кута АОВ (1 частина).

Відповідь: ∠АОВ = 30°.

Варіант 2

Завдання 1 За стовпчастою діаграмою, визнач кількість відмінників у 5– Г класі.

^{5–А — 2 в.}

^{5–Б — 4 в.}

^{5– В — 3 в.}

^{5–Г — 5 в.}

А 2 Б З В 4 Г 5

Завдання 2 Знайди градусну міру кута COD.

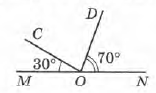
∠MON = 180° = ∠MOC + ∠COD + ∠NOD

∠COD = ∠MОN – ∠MОС – ∠NOD

∠COD = 180° – 30° – 70° = 80°

Відповідь: ∠COD = 80°

Завдання 3 Периметр рівнобедреного трикутника дорівнює Р см, а довжина основи — 12 см. Склади вираз для обчислення довжини бічної сторони трикутника. Знайди значення цього виразу, якщо Р = З0.

^{Короткий запис}

^{Бічні сторони — 2 сторони по ? см}

^{Основа — 12 см}

^{Р —}^{P см}

Розв’язання

^{P – 12 (см) – сума довжин двох бічних сторін (бічні сторони рівнобедреного трикутника рівні).}

(P – 12) : 2 (см) – довжина бічної сторони рівнобедреного трикутника.

Якщо P = 30, тоді (P – 12) : 2 = (30 – 12) : 2 = 18 : 2 = 9 (см)

Відповідь: 9 см.

Завдання 4 Кут КОМ удвічі менший за кут MON. Знайди градусну міру кута КОМ, якщо ∠KON = 90°.

∠KON = ∠KOM + ∠MON

Нехай х(°) – градусна міра кута KOM, тоді 2х (°) – градусна міра кута MON. Складемо рівняння.

х + 2х = 90

9х = 90

х = 90 : 3

х = 30 (°) – градусна міра кута KOM.

2 спосіб

1) 1 + 2 = 3 (ч.) – частин складає кут KON.

2) 90 : 3 = 30 (°) – градусна міра кута KOM (1 частина).

Відповідь: ∠KOM = 30°.

Варіант З

Завдання 1 За стовпчастою діаграмою, визнач кількість гуртківців серед учнів 5–А класу.

^{5–А — 5 г.}

^{5–Б — 2 г.}

^{5– В — 3 г.}

^{5–Г — 4 г.}

А 2 Б З В 4 Г 5

Завдання 2 Знайди градусну міру кута MON.

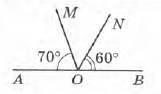
∠AOB = 180° = ∠AOM + ∠MON + ∠BON

∠MON = ∠АОВ – ∠АOМ – ∠ВON

∠MON = 180° – 70° – 60° = 50°

Відповідь: ∠MON = 50°

Завдання 3 Периметр рівнобедреного трикутника дорівнює 36 дм, а довжина основи — а см. Склади вираз для обчислення довжини бічної сторони трикутника. Знайди значення цього виразу, якщо а = 14.

^{Короткий запис}

^{Бічні сторони — 2 сторони по ? дм}

^{Основа —}^{a дм}

^{Р —}^{36 дм}

Розв’язання

^{36 –}^{a (дм) – сума довжин двох бічних сторін (бічні сторони рівнобедреного трикутника рівні).}

(36 – a) : 2 (дм) – довжина бічної сторони рівнобедреного трикутника.

Якщо a = 14, тоді (36 – a) : 2 = (36 – 14) : 2 = 22 : 2 = 11 (дм)

Відповідь: 11 дм.

Завдання 4 Кут COF у 4 рази менший за кут FOD. Знайди градусну міру кута COF, якщо ∠COD = 100°.

∠COD = ∠COF + ∠FOD

Нехай х(°) – градусна міра кута COF, тоді 4х (°) – градусна міра кута FOD. Складемо рівняння.

х + 4х = 100

5х = 100

х = 100 : 5

х = 20 (°) – градусна міра кута COF.

2 спосіб

1) 1 + 4 = 5 (ч.) – частин складає кут COD.

2) 100 : 5 = 20 (°) – градусна міра кута COF (1 частина).

Відповідь: ∠COF = 20°.

Варіант 4

Завдання 1 За стовпчастою діаграмою визнач кількість гуртківців серед учнів 5–В класу.

^{5–А — 5 г.}

^{5–Б — 2 г.}

^{5– В — 3 г.}

^{5–Г — 4 г.}

А 2 Б З В 4 Г 5

Завдання 2 Знайди градусну міру кута MON.

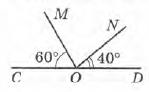
∠COD = 180° = ∠COM + ∠MON + ∠DON

∠MON = ∠СОD – ∠СOМ – ∠DON

∠MON = 180° – 60° – 40° = 80°

Відповідь: ∠MON = 80°

Завдання 3 Периметр рівнобедреного трикутника дорівнює Р дм, а довжина основи — 10 дм. Склади вираз для обчислення довжини бічної сторони трикутника. Знайди значення цього виразу, якщо Р = 28.

^{Короткий запис}

^{Бічні сторони — 2 сторони по ? дм}

^{Основа —}^{10 дм}

^{Р —}^{P дм}

Розв’язання

^{P – 1}^{0 (дм) – сума довжин двох бічних сторін (бічні сторони рівнобедреного трикутника рівні).}

(P – 10) : 2 (дм) – довжина бічної сторони рівнобедреного трикутника.

Якщо P = 28, тоді (P – 10) : 2 = (28 – 10) : 2 = 18 : 2 = 9 (дм)

Відповідь: 9 дм.

Завдання 4 Кут DOK у 4 рази менший за кут КОС. Знайди градусну міру кута DOK, якщо ∠DOC = 80°.

∠DOC = ∠DOK + ∠KOC

Нехай х(°) – градусна міра кута DOK, тоді 4х (°) – градусна міра кута KOC. Складемо рівняння.