Діагностична робота 5
Геометричні фігури і величини
Варіант 1
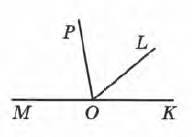
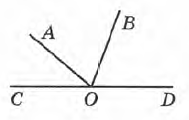
Завдання 1 Серед променів, зображених на малюнку, знайди пару доповняльних (доповняльні промені разом утворюють кут 180°).
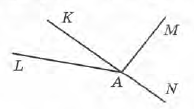
A. AM і AN
В. АК і AN
В. AL і AM
Г. АХ і AM
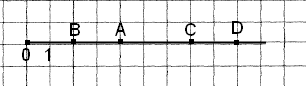
Завдання 2 Яке число відповідає точці С на малюнку?

А. 5
Б. 4
В. З
Г. 2
Завдання 3 На якому з малюнків зображено гострий кут (менший від 90°)?
А прямий
Б гострий
В розгорнутий
Г тупий
Завдання 4 Знайди площу прямокутника, одна зі сторін якого дорівнює 9 см, а інша є меншою від неї на 3 см.
|
А 135 см² Б 18 см² В 54 см² Г 27 см² |
Розв’язання 1) 9 – 3 = 6 (см) – ширина прямокутника. 2) S = 9 • 6 = 54 (см²) Відповідь: 54 см². |
Завдання 5 На відрізку ВС, довжина якого 50 см, позначено точки А і D так, що АВ = 18 см, DC = 12 см. Знайди довжину відрізка AD.
B_______A__________D_____C
Розв’язання
АD = ВС – АВ – DС = 50 – 18 – 12 = 20 (см)
Відповідь: АD = 20 см.
Завдання 6 Накресли координатний промінь і познач на ньому точки А(4), В(2), С(7), D(9)
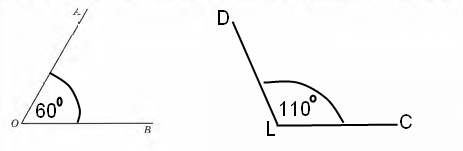
Завдання 7 Виміряй ∠AOB і побудуй ∠CLD, градусна міра якого на 50° більша за градусну міру кута АОВ. Підпиши на малюнку градусну міру кута CLD.
Розв’язання
∠CLD = ∠АОВ + 50° = 60° + 50° = 110°
Завдання 8 Сторони прямокутника дорівнюють 8 мм і 10 мм. Знайди площу квадрата, периметр якого дорівнює периметру даного прямокутника.
Розв’язання
1) Р = (8 +10) • 2 = 36 (мм) – периметр прямокутника (периметр квадрата);
2) 36 : 4 = 9 (мм) – довжина сторони квадрата;
3) S = 9 • 9 = 81 (мм²) – площа квадрата.
Відповідь: 81 мм².
Завдання 9 На малюнку ∠АОD = 120°; ∠COB = 130°. Знайди градусну міру кута COD.
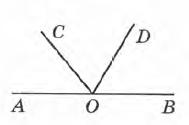
Розв’язання
1 спосіб
∠ВОD = ∠АОВ – ∠АОD = 180° – 120° = 60°
∠СОD = ∠СОВ – ∠ВОD = 130° – 60° = 70°
2 спосіб
∠АОС = ∠АОВ – ∠СОВ = 180° – 130° = 50°
∠СОD = ∠АОD – ∠АОС = 120° – 50° = 70°
3 спосіб
∠ВОD = ∠АОВ – ∠АОD = 180° – 120° = 60°
∠АОС = ∠АОВ – ∠СОВ = 180° – 130° = 50°
∠СОD = ∠АОВ – ∠BОD – ∠AОC = 180° – 60 ° – 50° = 70°
Відповідь: ∠СОD = 70°.
Варіант 2
Завдання 1 Серед променів, зображених на малюнку, знайди пару доповняльних (доповняльні промені разом утворюють кут 180°).
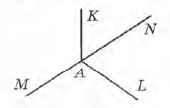
A. AM і AN
В. АК і AN
В. AL і AM
Г. АХ і AM
Завдання 2 Яке число відповідає точці М на малюнку?
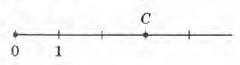
А. 5
Б. 4
В. З
Г. 2
Завдання 3 На якому з малюнків зображено тупий кут?
А прямий
В гострий
В розгорнутий
Г тупий
Завдання 4 Знайди площу прямокутника, одна зі сторін якого дорівнює 9 см, а інша є меншою від неї на 6 см.
|
А 135 см² Б 18 см² В 54 см² Г 27 см² |
Розв’язання 1) 9 – 6 = 3 (см) – ширина прямокутника. 2) S = 9 • 3 = 27 (см²) Відповідь: 27 см². |
Завдання 5
На відрізку ВС, довжина якого 60 см, позначено точки А і В так, що АС =15 см, ВК = 25 см. Знайди довжину відрізка КА.
B__________K______A_____C
Розв'язання
КА = ВС – АС – ВК = 60 см – 15 см – 25 см = 20 см
Відповідь: КА = 20 см
Завдання 6 Накресли координатний промінь і познач на ньому точки М(5), N(3), К(6), Р(10).
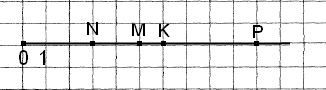
Завдання 7 Виміряй ∠COD і побудуй ∠ALD, градусна міра якого на 60° менша від градусної міри кута COD. Підпиши на малюнку градусну міру кута ALD.
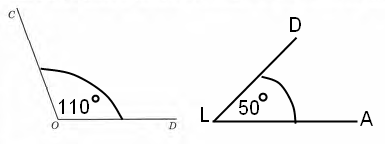
∠ALD = ∠COD – 60° = 110° – 60° = 50°
Завдання 8 Сторони прямокутника дорівнюють 6 см і 10 см. Знайди площу квадрата, периметр якого дорівнює периметру даного прямокутника.
Розв’язання
1) Р = (6 + 10) • 2 = 32 (см) – периметр прямокутника (периметр квадрата);
2) 32 : 4 = 8 (см) – довжина сторони квадрата;
3) S = 8 • 8 = 64 (см²) – площа квадрата.
Відповідь: 64 см².
Завдання 8. На малюнку ∠MOL = 140°; ∠KOP = 100°. Знайди градусну міру кута POL.
Розв’язання
1 спосіб
∠МОР = ∠МОК – ∠КОР = 180° – 100° = 80°
∠РОL = ∠МОL – ∠МОР = 140° – 80° = 60°
2 спосіб
∠КОL = ∠МОК – ∠МОL = 180° – 140° = 40°
∠РОL = ∠КОР – ∠КОL = 100° – 40° = 60°
3 спосіб
∠МОР = ∠МОК – ∠КОР = 180° – 100° = 80°
∠КОL = ∠МОК – ∠МОL = 180° – 140° = 40°
∠РОL = ∠МОК – ∠МОР – ∠КОL = 180° – 80 ° – 40° = 60°
Відповідь: ∠РОL = 60°
Варіант 3
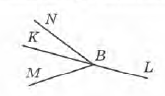
Завдання 1 Серед променів, зображених на малюнку, знайди пару доповняльних (доповняльні промені разом утворюють кут 180°).
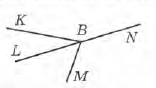
А. ВМ і BN
Б. ВК і ВМ
В. ВК і BL
Г. BL і BN
Завдання 3. Якому числу відповідає точка D на малюнку?

А. З
Б. 4
В. 5
Г. 6
Завдання 3 На якому з малюнків зображено прямий кут?
А тупий кут
Б розгорнутий кут
В прямий кут
Г гострий кут
Завдання 4 Знайди площу прямокутника, одна зі сторін якого дорівнює 8 см, а інша – на З см більша.
|
А 24 см² Б 40 см² В 88 см² Г 104 см² |
Розв’язання. 1) 8 + 3 = 11 (см) – довжина прямокутника. 2) S = 8 • 11 = 88 (см²) Відповідь: 88 см². |
Завдання 5 На відрізку РЕ, довжина якого 40 см, позначено точки А і К так, що РА = 17 см, КЕ =13 см. Знайди довжину відрізка АК.
P_________A____K______E
Розв'язання
AK = РЕ – РА – КЕ = 40 см – 17 см – 13 см = 10 см.
Відповідь: АК = 10 см.
Завдання 6. Накресли координатний промінь і познач на ньому точки К(7), L(5), N(2), М(9).
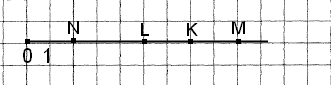
Завдання 7 Виміряй ∠МОК і побудуй ∠PLT, градусна міра якого на 60° більша за градусну міру ∠МОК. Підпиши на малюнку градусну міру кута МОК.
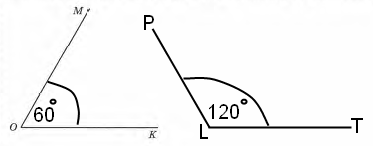
∠РLТ = ∠МОК + 60° = 60° + 60° = 120°
Завдання 8 Сторони прямокутника дорівнюють 7 дм і 5 дм. Знайди площу квадрата, периметр якого дорівнює периметру цього прямокутника.
Розв’язання
1) Р = (7 + 5) • 2 = 24 (дм) – периметр прямокутника (периметр квадрата);
2) 24 : 4 = 6 (дм) – довжина сторони квадрата;
3) S = 6 • 6 = 36 (дм²) – площа квадрата.
Відповідь: 36 дм².
Завдання 8. На малюнку ∠AOD = 140°; ∠COB = 110°. Знайди градусну міру кута AOВ.
Розв’язання
1 спосіб
∠ВОD = ∠СОD – ∠СОВ = 180° – 110° = 70°
∠АОВ = ∠АОD – ∠ВОD = 140° – 70° = 70°
2 спосіб
∠АОС = ∠СОD – ∠АОD = 180° – 140° = 40°
∠АОВ = ∠СОВ – ∠АОС = 110° – 40° = 70°
3 спосіб
∠ВОD = ∠СОD – ∠СОВ = 180° – 110° = 70°
∠АОС = ∠СОD – ∠АОD = 180° – 140° = 40°
∠АОВ = ∠СОD – ∠ВОD – ∠АОС = 180° – 70 ° – 40° = 70°
Відповідь: ∠АОВ = 70°
Варіант 4
Завдання 1 Серед променів, зображених на малюнку, знайди пару доповняльних (доповняльні промені разом утворюють кут 180°).
А. ВМ і BN
Б. ВК і ВМ
В. ВК і BL
Г. BL і BN
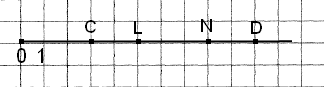
Завдання 2 Яке число відповідає точці D на малюнку?

А. З
Б. 4
В. 5
Г. 6
Завдання 3 На якому з малюнків зображено розгорнутий кут?
А. тупий
Б. розгорнутий
В. прямий
Г. гострий
Завдання 4 Знайди площу прямокутника, одна зі сторін якого дорівнює 8 см, а інша – на 5 см більша.
|
А 24 см² Б 40 см² В 88 см² Г 104 см² |
Розв’язання. 1) 8 + 5 = 13 (см) – довжина прямокутника. 2) S = 8 • 13 = 104 (см²) Відповідь: 104 см². |
Завдання 5 На відрізку AM, довжина якого 30 см, позначено точки В і С так, що АВ = 7 см, СМ = 13 см. Знайди довжину відрізка ВС.
A____B______C___________M
ВС = АМ – АВ – СМ = 30 см – 7 см – 13 см = 10 см
Відповідь: 10 см.
Завдання 6 Накресли координатний промінь і познач на ньому точки С(3), D(10), L(5), N(8).
Завдання 7 Виміряй ∠POС і побудуй ∠MLK, градусна міра якого на 50° менша від градусної міри кута РОС. Підпиши на малюнку градусну міру кута MLK.
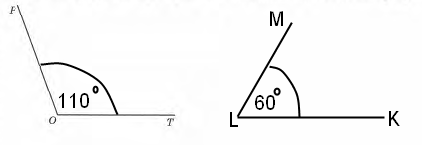
∠МLК = ∠РОC – 50° = 110° – 50° = 60°
Завдання 8 Сторони прямокутника дорівнюють 9 м і 7 м. Знайди площу квадрата, периметр якого дорівнює периметру прямокутника.
Розв’язання
1) Р = (9 + 7) • 2 = 32 (м) – периметр прямокутника (периметр квадрата);
2) 32 : 4 = 8 (м) – довжина сторони квадрата;
3) S = 8 • 8 = 64 (м²) – площа квадрата.
Відповідь: 64 м².
Завдання 9 На малюнку кут DOK = 150°; кут MOL = 100°. Знайди градусну міру кута МОК.
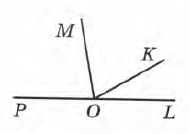
Розв’язання
1 спосіб
∠МОD = ∠DОL – ∠МОL = 180° – 100° = 80°
∠МОК = ∠DОК – ∠МОD = 150° – 80° = 70°
2 спосіб
∠КОL = ∠DОL – ∠DОК = 180° – 150° = 30°
∠МОК = ∠МОL – ∠КОL = 100° – 30° = 70°
3 спосіб
∠МОD = ∠DОL – ∠МОL = 180° – 100° = 80°
∠КОL = ∠DОL – ∠DОК = 180° – 150° = 30°
∠МОК = ∠DОL – ∠МОD – <КОL = 180° – 80° – 30° = 70°
Відповідь: ∠МОК = 70°