Завдання 691
1) Промені: DC, OK; Прямі: MN, c; Відрізок: AB
2) Промінь ОК і промінь DC не мають спільних точок. Промінь DC і пряма MN мають спільну точку.
3) Відрізок АВ і промінь ОK не перетинаються.
Відрізок АВ і пряма MN перетинаються.
Відрізок АВ і пряма с не перетинаються.
Завдання 692
Відрізки: AB; Прямі: MN; Промені: BM,AN.
Завдання 693
Відрізки: OL; Прямі: KN; Промені: OK, OM, LN, ON.
Завдання 694 Позначте деякі три точки, які:
1) лежать на одній прямій;
2) не лежать на одній прямій.
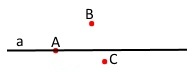
Завдання 695 Позначте точки С і D та проведіть через них пряму. Скільки утворилося променів із початками в точках С і D?
2 • 2 = 4 (промені)
Відповідь: 4 промені.
Завдання 696
Позначте точку O і проведіть дві прямі, що проходять через цю точку. Скільки утворилося променів із початком у точці О?
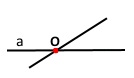
2 • 2 = 4 (промені)
Відповідь: 4 промені.
Завдання 697
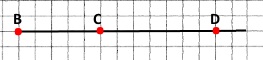
Накресліть промінь із початком у точці В. На промені позначте такі точки С і D, щоб ВС = 2 см 5 мм, ВD = 6 см. Знайдіть довжину відрізка CD.
CD = ВD – ВС = 6 см – 2 см 5 мм = 40 мм – 5 мм = 35 мм = 3 см 5 мм
Завдання 698. На промені OM позначено точки N і K так, що ON = 14 см, OK = 12 см. У скільки разів довжина відрізка OK більша за довжину відрізка KN?
KN = ON – OK = 14 см – 12 см = 2 см
OK : KN = 12 см : 2 см = 6
Відповідь: у 6 разів.
Завдання 699
Чи може спільною частиною двох променів бути точка? Може (два промені зі спільної точки в направлені у протилежні напрямки).
Відрізок? Може (два промені з різних точок направлені назустріч).
Промінь? Може (один промінь знаходиться на іншому).
Пряма? Ні.
Завдання 700 Перерисуйте в зошит пряму b і точки, зображені на рисунку 72. Проведіть усі промені з початками в даних точках, кожний з яких проходив би через іншу задану точку й не перетинав пряму b.
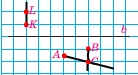
Завдання 701. Перерисуйте в зошит пряму а й точки, зображені на рисунку 73. Проведіть усі ті відрізки з кінцями в даних точках, які перетинають пряму а. Скільки отримали відрізків?
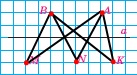
Відповідь: 6 відрізків.
Завдання 702 На прямій позначили 5 точок. Скільки утворилося променів з початками в цих точках?
![]()
2 • 5 = 10 (променів)
Відповідь: 10 променів.
Завдання 703
Будинки Антона, Бориса, Валентини та Галини розташовані вздовж прямолінійного шляху в указаній послідовності (рис. 74). Відомо, що відстань від будинку Антона до будинку Галини дорівнює 140 м, від будинку Бориса до будинку Валентини — 50 м. До того ж, Валентині до будинку Галини потрібно пройти удвічі більшу відстань, ніж Борису до будинку Антона. Знайдіть відстань між будинками Антона та Валентини.
Розв'язання
1) 140 – 50 = 90 (м) – відстань між АБ і ВГ
2) 90 : 3 = 30 (м) – відстань між АБ
3) 30 + 50 = 80 (м) – відстань між АВ
Відповідь: 80 метрів.
Завдання 704
Відстань між двома автомобілями, які рухаються трасою в одному напрямку, дорівнює 5 км. Якою буде відстань між автомобілями, якщо один з них проїде 8 км, а другий — 10 км? Знайдіть два варіанти відповіді.
1 спосіб
1) 5 + 8 = 13 (км) – відстань першого.
2) 13 – 10 = 3 (км) – відстань між ними.
2 спосіб
1) 10 + 5 = 15 (км) – відстань другого.
2) 15 – 8 = 7 (км) – відстань між ними.
Завдання 705
Десять точок лежать на одній прямій. Скільки існує відрізків з кінцями в цих точках?
Позначимо точки: 1, 2, 3, 4, 5, 6, 7, 8, 9, 0, тоді
12, 13, 14, 15, 16, 17, 18, 19, 10
23, 24, 25, 26, 27, 28, 29, 20
34, 35, 36, 37, 38, 39, 30
45, 46, 47, 48, 49, 40
56, 57, 58, 59, 50
67, 68, 69, 60
78, 79, 70
89, 80
90
Відповідь: 45 відрізків.
Вправи для повторення
Завдання 706 Порівняйте числа
|
1) 500 382 < 509 143
|
2) 3 212 140 > 3 212 014
|
Завдання 707
Щоб обклеїти стіни кімнат гуртожитку, потрібно 485 м шпалер. Яку найменшу кількість рулонів шпалер потрібно для цього купити, якщо довжина одного рулону дорівнює 10 м?
Розв'язання
485 : 10 = 48 (ост. 5) – потрібно купити.
Відповідь: 49 рулонів.
Завдання 708
Із міста виїхав велосипедист, а через 2 год вслід за ним — автомобіль. Швидкість автомобіля дорівнює 75 км/год, а велосипедиста — 25 км/год. Чи встигне автомобіль за годину руху наздогнати велосипедиста?
Розв'язання
1) 25 • 2 = 50 (м) – проїхав велосипедист.
2) 75 – 25 = 50 (м/год) – швидкість зближення.
3) 50 : 50 = 1 (год) – через стільки часу автомобіль наздожене велосипедиста.
Відповідь: встигне.
Завдання 709 Знайдіть усі можливі значення а, для яких число 49 при діленні на а дає в остачі 4.
Розв'язання
49 : а = х (ост. 4)
х • а + 4 = 49
х • а = 49 – 4
х • а = 45
1 • 45 = 45
3 • 15 = 45
9 • 5 = 45
5 • 9 = 45
Відповдіь: а = 45, 15, 5, 9.