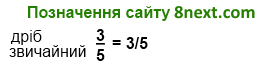
Завдання 502
Родина пливе річкою на байдарці, не використовуючи весел, зі швидкістю 3 км/год. Яка швидкість течії річки?
Як ти вважаєш, чи пливтиме човен у ставку, де течія відсутня? А чи пливтиме в ставку моторний катер з увімкненим мотором?
Що треба зробити, щоб човен плив за течією річки швидше, ніж швидкість течії річки?
Із чого складається швидкість руху човна, який пливе за течією річки?
Як ти вважаєш, якщо човен пливтиме проти течії річки, то швидкість його руху буде більшою чи меншою, ніж його власна швидкість?
Завдання 503
Відстань між пристанями А і В, що розташовані на річці, 160 км . За який час катер пройде відстань від пристані А до пристані В й повернеться, якщо власна швидкість руху катера 13 км/год, а швидкість течії річки 3 км/год? На скільки більше часу катер витратить на рух проти течії річки, ніж на рух за течією річки?
Розв'язання
1) 13 + 3 = 16 (км/год) – швидкість катера за течією річки;
2) 13 – 3 = 10 (км/год) – швидкість катера проти течії річки;
3) 160 : 16 = 10 (год) – час руху катера за течією річки;
4) 160 : 10 = 16 (год) – час руху катера проти течії річки;
5) 16 – 10 = 6 (год) – на стільки год більше катер витратить на рух проти течії, ніж за течією.
Відповідь: на 6 год більше.
Завдання 504
Велосипедист рухається за вітром зі швидкістю 14 м/с. Знайди власну швидкість руху велосипедиста, якщо швидкість вітру 4 м/с .
Розв'язання
14 – 4 = 10 (м/с) – власна швидкість руху велосипедиста.
Відповідь: 10 м/с.
Обернена задача на знаходження швидкості велосипедиста за вітром.
Власна швидкість велосипедиста 10 м/с. Знайдіть швидкість руху велосипедиста за вітром, якщо швидкість вітру 4 м/с.
Розв'язання
10 + 4 = 14 (м/с) – швидкість велосипедиста за вітром.
Відповідь: 14 м/с.
Обернена задача на знаходження швидкості вітру.
Велосипедист рухається за вітром зі швидкістю 14 м/с. Знайди швидкість вітру, якщо власна швидкість руху велосипедиста 10 м/с .
Розв'язання
14 – 10 = 4 (м/с) – швидкість вітру.
Відповідь: 4 м/с.
Завдання 505
Мотодельтаплан летить проти вітру зі швидкістю 5 м/с. Знайди швидкість вітру, якщо власна швидкість руху мотодельтаплану 9 м/с .
Розв'язання
9 – 5 = 4 (м/с) – швидкість вітру.
Відповідь: 4 м/с.
Обернена задача на знаходження власної швидкості мотодельтаплану.
Мотодельтаплан летить проти вітру зі швидкістю 5 м/с. Знайди власну швидкість мотодельтаплану, якщо швидкість вітру 4 м/с .
Розв'язання
5 + 4 = 9 (м/с) – власна швидкість мотодельтаплану.
Відповідь: 9 м/с.
Обернена задача на знаходження швидкості руху проти вітру мотодельтаплану.
Власна швидкість мотодельтаплану 9 м/с. Знайди швидкість руху мотодельтаплану проти вітру, якщо швидкість вітру 4 м/с .
Розв'язання
9 – 4 = 5 (м/с) – швидкість руху мотодельтаплану проти вітру.
Відповідь: 5 м/с.
Завдання 506
Знайди швидкість руху катера за течією та проти течії річки, якщо власна швидкість руху катера 30 км/год, а швидкість течії річки — 5 км/год.
Розв'язання
1) 30 + 5 = 35 (м/с) – швидкість руху катера за течією річки;
2) 30 – 5 = 25 (м/с) – швидкість руху катера проти течії річки.
Відповідь: 35 м/с і 25 м/с.
Завдання 507
Власна швидкість руху гідроцикла 45 км/год, а швидкість течії річки — 4 км/год . Яку відстань подолає гідроцикл за 2 год, рухаючись за течією річки? проти течії річки?
Розв'язання
1) 45 + 4 = 49 (км/год) – швидкість руху гідроцикла за течією річки;
2) 45 – 4 = 41 (км/год) – швидкість руху гідроцикла проти течії річки;
3) 49 • 2 = 98 (км) – відстань подолав за течією річки;
4) 41 • 2 = 82 (км) – відстань подолав проти течії річки.
Відповідь: 98 км і 82 км.
Завдання 508
У Тетяни було 5 горіхів. Коли вона віддала брату один горіх, у дітей стало горіхів порівну . Скільки горіхів було в брата Тетяни?
Розв'язання
1) 5 – 1 = 4 (г.) – стало порівно;
2) 4 – 1 = 3 (г.) – було в брата Тетяни.
Відповідь: 3 горіхи.
Завдання 509
Моторний човен за 40 хв подолав озером 8 км, а річкою за 2 год — 42 км, причому мотор човна весь час працював з однаковою потужністю . Знайди швидкість течії річки.
Розв'язання
8 км = 8000 м; 42 км = 42 000 м; 2 год = 120 хв
1) 8000 : 40 = 200 (м/хв) – власна швидкість човна;
2) 42 000 : 120 = 350 (м/хв) – швидкість човна за течією річки;
3) 350 – 200 = 150 (м/хв) – швидкість течії річки.
Відповідь: 150 м/хв.
Завдання 510
1) Швидкість руху човна за течією річки на 300 м/хв більша, ніж проти течії . Яка швидкість течії річки?
300 : 2 =150 (м/хв) – швидкість течії річки.
2) Швидкість руху човна за течією річки 350 м/хв, а проти течії — 50 м/хв . Знайди швидкість течії річки.
(350 – 50) : 2 = 150 (м/хв) – швидкість течії річки.
Завдання 511
1) Швидкість руху плавця в басейні — 4 км/год, а в річці — 8 км/год . Знайди швидкість течії річки.
Розв'язання
8 – 4 = 4 (км/год) – швидкість течії річки.
Відповідь: 4 км/год.
2) Швидкість руху скутериста проти вітру — 24 км/год . Знайди власну швидкість скутериста, якщо швидкість вітру 11 км/год.
Розв'язання
24 – 11 = 13 (км/год) – власна швидкість скутериста.
Відповідь: 13 км/год.
3) Швидкість руху катера за течією річки — 22 м/с, а проти течії — 20 м/с . Знайди швидкість течії річки.
Розв'язання
(22 – 20) : 2 = 1 (м/с) – швидкість течії річки.
Відповідь: 1 м/с.
Завдання 512
Між двома пристанями А і В, відстань між якими 300 км, ходить рейсовий катер. Власна швидкість руху катера — 55 км/год . За скільки годин він пройде відстань від пристані А до пристані В і повернеться, якщо швидкість течії річки 5 км/год?
Розв'язання
1) 55 + 5 = 60 (км/год) – швидкість руху катера за течією річки;
2) 55 – 5 = 50 (км/год) – швидкість руху катера проти течії річки;
3) 300 : 60 = 5 (год) – час руху катера за течією річки;
4) 300 : 50 = 6 (год) – час руху катера проти течії річки;
5) 5 + 6 = 11 (год) – весь час руху катера.
Відповідь: 11 год.
Завдання 513
Моторний човен пропливає 30 км, рухаючись за течією річки, за 2 год, а проти течії — за 3 год . Яка швидкість руху човна за течією річки? проти течії річки? Знайди швидкість течії річки.
1) 30 : 2 = 15 (км/год) – швидкість човна за течією річки;
2) 30 : 3 = 10 (км/год) – швидкість човна проти течії річки.
Завдання 514
Човен пропливає 15 км, рухаючись за течією річки, за 60 хв, а проти течії — за 75 хв. Яка швидкість течії?
Розв'язання
1) 15 : 60 = 15/60 = 1/4 (км/хв) – швидкість руху човна за течією річки;
2) 15 : 75 = 15/75 = 1/5 (км/хв) – швидкість руху човна проти течії річки.
3) (1/4 – 1/5) : 2 = (5/20 – 4/20) : 2 = 1/20 : 2 = 1/20 • 1/2 = 1/40 (км/хв)
Відповідь: швидкість течії річки 1/40 км/год.