|
Точки |
А(–2;3) |
В(4;0) |
С(12;–5) |
D(0;8) |
|
Абсциса |
–2 |
4 |
12 |
0 |
|
Ордината |
3 |
0 |
–5 |
8 |
Завдання 1538
|
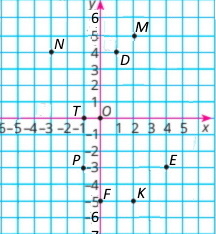
1) абсцису 4 має точка B(4;2) 3) абсцису 2 має точка A(2;–3) |
2) ординату 5 має точка C (–3;5) 4) ординату 4 має точка D(5;4) |
Завдання 1539
|
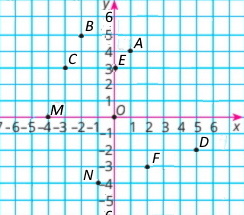
1) абсцису –4 має точка B(–4;–5) 3) абсцису 3 має точка M(3;–4) |
2) ординату 2 має точка S(–5;2) 4) ординату 3 має точка F(2;3) |
Завдання 1540, 1541
|
|
|
Завдання 1542
Координати точок: D(3;0); C(1;3); K(0;4); A(–2;5); H(–4;3); Q(–3;0); B(–5;–1); L(–3;3);
E(0;–3); F(3;–2)
Завдання 1543
Координати точок: G(5;0); F(2;2); L(4;4); A(0;5); B(–3;2); K(–5;0); E(–4;–2); D(0;–2);
H(2;–3); C(3;–1)
Завдання 1544
1) належать осі абсцис дві точки з координатами (5;0); (–2;0)
2) належать осі ординат дві точки з координатами (0;–4); (0;3)
3) мають абсцису –2 дві точки з координатами (–2;–1); (–2;5)
4) мають ординату 4 дві точки з координатами (–1;4); (3;4)
Завдання 1545
1) абсцису 7 мають три точки (7;8); (7;–5); (7;0)
2) ординату –3 мають три точки (0;–3); (2;–3);(–4;–3)
Завдання 1546
1) Координати точок: A(2;2); B(0;3); C(1;–1); D(–2;1); M(–3;–1); K(3;0)
2) Абсциси точок А, К, D: 2; 3; –2;
3) Ординати точок B, C, M: 3; –1; –1;
4) Ординату 0 має точка: K;
5) Абсцису 0 має точка: B;
6) Однакові ординати мають точки: M і С.
Завдання 1547
Туристи склали маршрут походу (мал. 99), старт і фініш якого в точці O, а зупинки в точках А, В, C, N i E. Довжині однієї клітинки відповідає 1 км.
О → 2 км на схід (точка А) → 2 км на південь (точка В) → 5 км на захід (точка С) → 3 км на північ (точка N) → 3 км на схід (точка Е) → 1 км на південь (точка О).
Завдання 1548
Координати точок: А(3;–3); B(3;2); C(–3;2); D(–3;3); E(5;2); F(0;4); G(–5;2)
Завдання 1549
Координати точок: А(–5;0); B(5;0); C(4;–2); D(–4;–2); E(0;4); F(0;5); G(2;5); H(2;4)
Завдання 1550
|
Будинок |
А |
В |
С |
D |
|
Від шосе Ох, одиниць |
3 |
1 |
2 |
1 |
|
Від шосе Оу, одиниць |
2 |
3 |
2 |
4 |
Завдання 1551, 1552
|
А(1;4), В(-2;5), С(-3;3), D(5;-2), Е(0;3), F(2;-3), М(-4;0), N(-1;-4)
|
М(2;5), N(-3;4), К(2;-5), Р(-1;-3), F(О;-5), Е(4;-3), Т(-1;0), D(1;4)
|
Завдання 1553, 1554
|
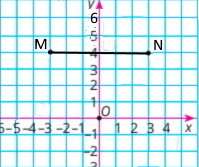
Точки М(–;3;4 ) і N(3;4). Координата (0;4) — середина MN.
|
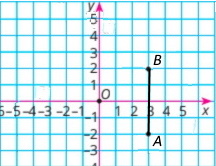
Точки А(3; –2) і В(3;2). Координата (3;0) — середина AB.
|
Завдання 1555, 1556
|
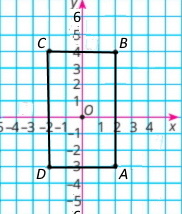
А(2;–3), В(2;4), С (–2;4), D (–2;–3) Чотирикутник є прямокутником.
|
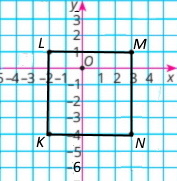
К(–2;–4), L(–2;1), М(3;1), N(3;–4) Чотирикутник є квадратом.
|
Завдання 1557, 1558
|
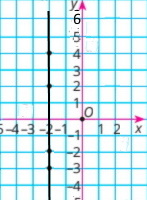
Чотири точки з абсцисами –2. Ці точки лежать на одній прямій.
|
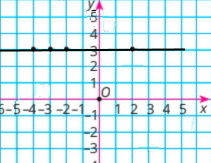
Чотири точки з ординатами 3. Ці точки лежать на одній прямій.
|
Завдання 1559
|
Точка |
А(–3;7) |
В(0,9;0,4) |
С(–1/5;–2/7) |
D(7,9;–12,5) |
|
Чверть |
II |
I |
III |
IV |
Завдання 1560
|
Точка |
А(–7;–1) |
В(14;–9) |
С(–0,4;0,05) |
D(1/17;1 1/8) |
|
Чверть |
III |
IV |
II |
I |
Завдання 1561
|
1) x > 0; y < 0; М(х; у) – IV чверть 3) х < 0; у > 0; М(х; у) – ІІ чверть |
2) x > 0; y > 0; М(х; у) – I чверть 4) x < 0; y < 0; М(х; у) – IІІ чверть |
Завдання 1562, 1563
|
Прізвища українських поетів |
Назви міст України |
|
1) СТУС 2) ДРАЧ 3) ТИЧИНА 4) КОСТЕНКО |
1) КИЇВ 2) ЛЬВІВ 3) ДОНЕЦЬК 4) ОДЕСА |
Завдання 1564
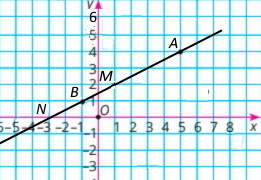
Точки Е(6;6), М(–2;2), N(4;1), Р(–2;4). Координати точок перетину:
1) прямих EM і NP: B(0;3)
2) прямої EM з віссю абсцис: A(–5;0)
3) прямої NP з віссю ординат: B(0;3).
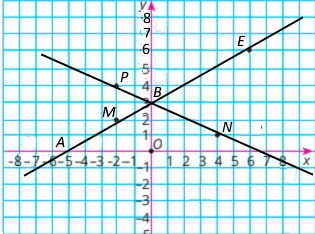
Завдання 1565
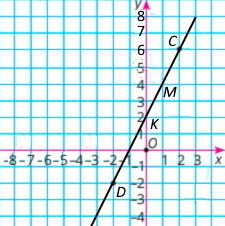
Точки А(–8;1), В(2;–6), С(4;7), D(–8;9). Координати точки перетину:
1) прямих AC і BD: L(–4;3)
2) прямої AC з віссю абсцис: M(–10;0)
3) прямої BD з віссю ординат: N(0;–3)
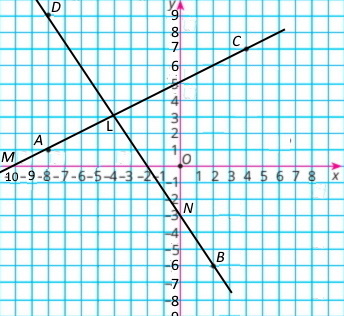
Завдання 1566
Точки М (5;–3), N(4;2) і К (–1;2), промені MN і MK.
Градусна міра кута: ∠NMK = 32°
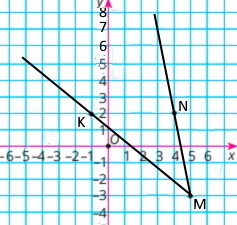
Завдання 1567
Точки М(0;6), N(12;2) і К(–8;–2); промені MN і МК.
Градусна міра кута: ∠NMK = 115°
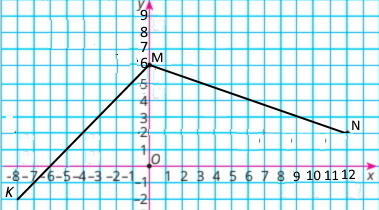
Завдання 1568
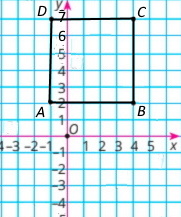
1) Чотирикутник KLMN називають квадрат
2) Координати вершин: К(3;–2); L(–1;–2); М(–1;2); N (3;2)
3) Площа: S = 4² = 16 (од.²). Периметр: Р = 4 • 4 = 16 (од.)
Завдання 1569
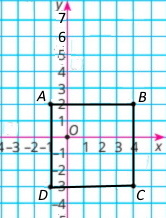
1) Чотирикутник АВСD називають прямокутник
2) Координати вершин: А(–1;2); В (3;2); С (3;–4); D (–1;–4)
3) Площа: S = 4 • 6 = 24 (од.²). Периметр: Р = (4 + 6) • 2 = 20 (од.)
Завдання 1570, 1571
|
Точки А(5;4) і В(–1;1) 1) точка, з абсцисою 1: М(1;2) 2) точка з ординатою 0: N(–3;0)
|
Точки С(2;6) і D (–2;–2) 1) точка з абсцисою 0: К(0;2) 2) точка з ординатою 4: M(1;4)
|
Завдання 1572
Координати трьох вершин прямокутника ABCD: А(–4;1), В(2;1), С(2;–3).
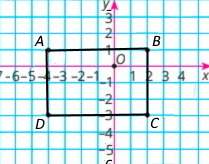
2) Координати точки D(–4;–3)
3) Координати точки перетину відрізків AC і BD (діагоналей прямокутника): Q(–1;–1)
4) Площа: S = 4 • 6 = 24 (од.²). Периметр прямокутника: P = 2(4 + 6) = 20 (од.)
Завдання 1573
Дано координати двох вершин квадрата ABCD: А (–1;2) і В(4;2)
| Випадок 1 |
Випадок 2 |
|
|
|
2) Координати точок С(4;–3); D(–1;–3) або С(4;7); D(–1;7)
3) Площа: S = 5² = 25 (од.²). Периметр: Р = 4 • 5 = 20 (од.)
Завдання 1574
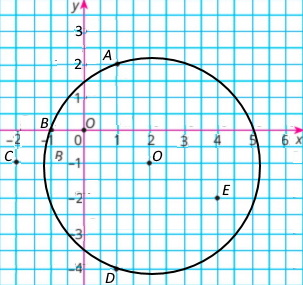
Коло із центром у точці О(2;–1) проходить через точку А(1;2).
Точка B і D – належить колу; точки Е і С – не належать колу.
Завдання 1575
Замкнена ламана, послідовними вершинами якої є точки з координатами: (1;7), (0;10),
(–1;11), (–2;10), (0;7), (–2;5), (–7;3), (–8;0), (–9;1), (–9;0), (–7;–2), (–2;–2), (–3;–1),
(–4;–1), (–1;3), (0;–2), (1;–2), (0;0), (0;3), (1;4), (2;4), (3;5), (2;6), (1;9), (0;0) та (1;6).
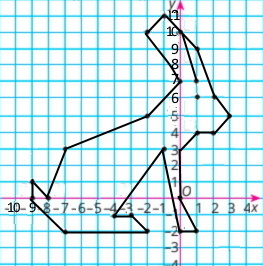
Намальована тварина: зайченя
Завдання 1576
Дві замкнені ламані, послідовними вершинами яких є точки з координатами: (4;–1),
(7;–2), (–2;–3), (–10;4), (–3;2), (1;5), (8;3), (7;–2) і (–10;4), (–12;6), (–9;9), (–12;8),
(–15;9), (–12;6). Познач точку (4;2).
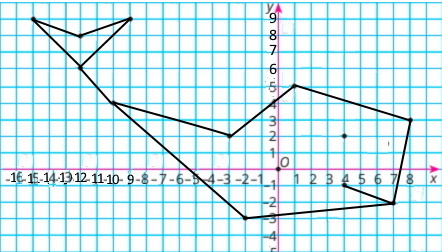
Намальована тварина: кит.
Завдання 1577
Познач на координатній площині всі точки, у яких абсциса й ордината — невід’ємні числа, а їхня сума дорівнює 5. Яку фігуру утворять ці точки?
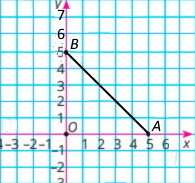
Точки утворюють відрізок АВ з кінцями в точках А(5;0) і В(0;5).
Завдання 1578
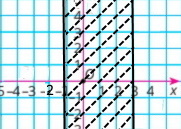
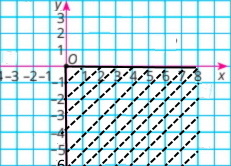
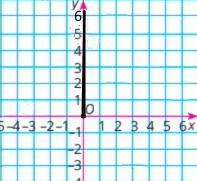
Зобрази на координатній площині множину точок (х; у) таких, що:
|
1) –1 ≤ х ≤ 3, у — довільне;
|
2) х ≥ 0, у ≤ 0;
|
|
3) х = 0, у ≥ 0;
|
4) |х| ≤ 1, |у|≤ 2.
|
Завдання 1579
1) 5 кг від 1 ц — це 5 : 100 • 100% = 5%
2) 12 см від 2 м — це 12 : 200 • 100% = 6%
3) 24 хв від 1 год — це 24 : 60 • 100% = 40%
4) 36 с від 1 хв — це 36 : 60 • 100% = 60%
Завдання 1580 Вирази
(2х – у) + (у – 3х) – (2у – 4х) = 2х – у + у – 3х – 2у + 4х = 3х – 2у
Якщо х = 2 1/3; у = –3 1/2, тоді 3х – 2у = 3 • 2 1/3 – 2 • (–3 1/2) = 3 • 7/3 – 2 • (–7/2) = 7 + 7 =
= 14
Завдання 1581
2(3х – 5у) – 5(2х – 4у) = 6x – 10у – 10х + 20у = –4x + 10у = 10у – 4x = 2 • 5у – 2 • 2х =
= 2 • (5у – 2х)
Якщо 5у – 2х = –17, тоді 2 • (5у – 2х) = 2 • (–17) = –34
Завдання 1582
Ipa щодня випиває 150 г свіжовичавленого соку. У 100 г соку міститься 12 г вуглеводів. Скільки вуглеводів Ipa споживає щодня, випиваючи сік?
Розв'язання
х • 100 = 150 • 12
х = (150 • 12 ) : 100
х = (1800 ) : 100
х = 18 (г) – вуглеводів споживає Іра щодня, випиваючи сік.
Відповідь: 18 г.
Завдання 1583
У шести коробках лежать кульки: у першій — 1, у другій — 2, у третій — 3, у четвертій — 4, у п’ятій — 5, у шостій — 6. За один хід дозволяється в будь–які дві коробки додати по одній кульці. Чи можна за кілька ходів зрівняти кількість кульок у всіх коробках?
Спочатку у всіх коробках 1 + 2 + 3 + 4 + 5 + 6 = 21 кулька. Після k ходів їх стане 21 + 2k. З іншого боку, загальна кількість кульок у коробках у момент коли в усіх коробках однакова кількість кульок, дорівнює 6n, де n — кількість кульок в одній коробці. Звідси 21 + 2k = 6n, де k і n, — натуральні числа. Права частина останньої рівності – парне число, а ліва — непарне. Тому така рівність неможлива.
Відповідь: не можна.