Внаслідок аварії на Чорнобильській АЕС забруднено 6,6 млн га сільськогосподарських угідь. Оціни відсоток цих угідь від площі всіх сільськогосподарських угідь України, що дорівнює близько 42 млн га.
Розв'язання
42 млн га — 100 %
6,6 млн га — х %
42/6,6 = 100/12; х = 6,6 • 100 : 42 = 15,7 (%)
Відповідь: забруднено 15,7% угідь.
Завдання 180 На скільки відсотків
|
а) число 25 більше від числа 20
|
б) число 20 менше від числа 25
|
|
Розв'язання
1 спосіб
1) 25 – 20 = 5 – різниця чисел.
2) 5/20 • 100% = 25%
2 спосіб
20 — 100 %
25 — х %
20/25 = 100/х; х = 25 • 100 : 20 = 125 (%)
125% – 100% = 25%
Відповідь: на 25%.
|
Розв'язання
1 спосіб
1) 25 – 20 = 5 – різниця чисел.
2) 5/25 • 100% = 20%
2 спосіб
25 — 100 %
20 — х %
25/20 = 100/х; х = 20 • 100 : 25 = 80 (%)
100% – 80% = 20%
Відповідь: на 20%.
|
Завдання 181
Якщо споживання лампи розжарювання за рік складає 394 кВт•год, то LED-лампи — 53 кВт•год. Який відсоток електроенергії вдасться зекономити, якщо всі лампи розжарювання в квартирі замінити на LED-лампи? Округли до цілої кількості відсотків.
Розв'язання
394 кВт — 100 %
53 кВт — х %
394/53 = 100/х; х = 53 • 100 : 394 = 14 (%)
100% – 14% = 86%
Відповідь: вдасться зекономити 86%.
Завдання 182
На скільки відсотків збільшиться число від збільшення його:
а) у 2 рази;
а — 100 %
2а — х %
а/2а = 100/х; х = 2а • 100 : а = 200 (%)
200% – 100% = 100%
Відповідь: на 100%.
б) у 1,6 рази;
а — 100 %
1,6а — х %
а/1,6а = 100/х; х = 1,6а • 100 : а = 160 (%)
160% – 100% = 60%
Відповідь: на 60%.
в) у 10 разів?
а — 100 %
10а — х %
а/10а = 100/х; х = 10а • 100 : а = 1000 (%)
1000% – 100% = 900%
Відповідь: на 900%.
Завдання 183
На скільки відсотків зменшиться число від зменшення його:
а) у 2 рази;
а — 100 %
0,5а — х %
а/0,5а = 100/х; х = 0,5а • 100 : а = 50 (%)
100% – 50% = 50%
Відповідь: на 50%.
б) у 1,6 рази;
а — 100 %
а/1,6 (0,625а) — х %
а/0,625а = 100/х; х = 0,625а • 100 : а = 62,5 (%)
100% – 62,5% = 37,5%
Відповідь: на 37%.
в) у 10 разів?
а — 100 %
а/10 (0,1а) — х %
а/0,1а = 100/х; х = 0,1а • 100 : а = 10 (%)
100% – 10% = 90%
Відповідь: на 90%.
Завдання 184
Перше число становить 40 % від другого. Скільки відсотків становить друге число від першого?
Розв'язання
Нехай друге число а, тоді перше число 0,4а.
а/0,4а • 100% = 2,5 • 100% = 250%
Відповідь: 250% друге число становить від першого.
Завдання 185
Число а становить 20% від числа b. Скільки відсотків число b становить від числа а?
Розв'язання
За умовою а = 0,2b, тому b/0,2b • 100% = 1/0,2 • 100% = 5 • 100% = 500%
Відповідь: 500%.
Завдання 186
Оля за першу хвилину пробігла 250 м, за другу — на 60 % цієї відстані більше. Який відсоток всієї відстані вона пробігла за третю хвилину, якщо весь її шлях становить 1 км?
Розв'язання
1) 250 • 0,6 = 400 (м) – пробігла за другу хвилину;
2) 250 + 400 = 650 (м) – пробігла за перші дві хвилини;
3) 1000 – 650 = 350 (м) – пробігла за третю хвилину.
4) 350 : 1000 • 100% = 35%
Відповідь: за третю хвилину вона пробігла 35% всієї відстані.
Завдання 187
Щомісячний прибуток сім’ї становить 23 000 грн. У березні витрати на харчування склали 9200 грн, а на оплату комунальних послуг — 3450 грн. На скільки відсотків більше було витрачено грошей на харчування, ніж на комунальні послуги?
Розв'язання
1) 9200 : 23 000 • 100% = 40% – витрати на харчування;
2) 3450 : 23 000 • 100% = 15% – витрати на комунальні послуги.
3) 40% – 15% = 25%
Відповідь: на 25% більше було витрачено грошей на харчування, ніж на комунальні послуги.
Завдання 188
Вкладник поклав у банк 60 000 грн під 8 % річних. Яку суму він матиме на рахунку через рік?
Розв'язання
1) 60000 • 1,08 = 64800 (грн) – сума через рік;
2) 64800 • 1,08 = 69984 (грн) – сума через два роки.
Відповідь: 64800 грн; 69984 грн.
Завдання 189
Вкладниця поклала у банк 50 000 грн під 9% річних. Яка сума буде на її рахунку через рік? Через два роки, якщо банк нараховує відсотки на відсотки?
Розв'язання
1) 50000 • 1,09 = 54500 (грн) – сума через рік;
2) 54500 • 1,09 = 69405 (грн) – сума через два роки.
Відповідь: 54500 грн; 69405 грн.
Завдання 190
На скільки відсотків збільшиться площа прямокутника, якщо одну з його сторін збільшити на 10 %, а другу — на 20 %? Розглянь випадки, коли сторони прямокутника дорівнюють:
а) 2 см і 5 см;
Розв'язання
1) 2 • 5 = 10 (см²) – площа прямокутника;
2) 2 • 1,1 = 2,2 (см) – збільшена ширина;
3) 5 • 1,2 = 6 (грн) – збільшена довжина;
4) 6 • 2,2 = 13,2 (см²) – площа збільшеного прямокутника;
5) 13,2 – 10 = 3,2 (см²) – на стільки змінилася площа.
6) 3,2/10 • 100% = 32%
Відповідь: на 32%.
б) 12 м і 25 м;
1) 12 • 25 = 300 (см²) – площа прямокутника;
2) 12 • 1,1 = 13,2 (см) – збільшена ширина;
3) 25 • 1,2 = 30 (см) – збільшена довжина;
4) 30 • 13,2 = 396 (см²) – площа збільшеного прямокутника;
5) 396 – 300 = 96 (см²) – на стільки змінилася площа.
6) 96/300 • 100% = 32%
Відповідь: на 32%.
в) x м і y м.
1) х • у = ху (см²) – площа прямокутника;
2) х • 1,1 = 1,1х (см) – збільшена ширина;
3) у • 1,2 = 1,2у (см) – збільшена довжина;
4) 1,1х • 1,2у = 1,32ху (см²) – площа збільшеного прямокутника;
5) 1,32ху – ху = 0,32ху (см²) – на стільки змінилася площа.
6) 0,32ху/ху • 100% = 32%
Відповідь: на 32%.
Відповідь від заданих довжин сторін не залежить.
Завдання 191
Валіза коштувала 900 грн. Спочатку її ціну підвищили на 20%, а потім знизили на 10%. Якою стала ціна валізи після цих змін? На скільки відсотків змінилася її початкова ціна?
Розв'язання
900 грн — 100 %
х грн — 120 %
900/х = 100/120; х = 900 • 120 : 100 = 1080 (грн) – ціна після підвищення;
1080 грн — 100 %
х грн — 90 %
1080/х = 100/90; х = 90 • 1080 : 100 = 972 (грн) – ціна після зниження.
900 грн — 100 %
972 грн — х %
900/972 = 100/х; х = 972 • 100 : 900 = 108 (%)
108% – 100% = 8%
Відповідь: на 8% збільшилася ціна.
Завдання 192
Спідниця коштувала 600 грн. Спочатку її ціну знизили на 20%, а потім підвищили на 15%. Якою стала ціна спідниці після цих змін? На скільки відсотків змінилася її початкова ціна?
Розв'язання
600 грн — 100 %
х грн — 80 %
600/х = 100/80; х = 600 • 80 : 100 = 480 (грн) – ціна після зниження;
480 грн — 100 %
х грн — 115 %
480/х = 100/115; х = 480 • 115 : 100 = 552 (грн) – ціна після підвищення.
600 грн — 100 %
552 грн — х %
600/552 = 100/х; х = 552 • 100 : 600 = 92 (%)
100% – 92% = 8%
Відповідь: на 8% зменшилася початкова ціна.
Завдання 193
Сайт підвищив плату за рекламу на 20 %, а потім нову ціну знизив на 10 %. На скільки відсотків зросла початкова ціна реклами?
Розв'язання
а грн — 100 %
х грн — 120 %
а/х = 100/120; х = 120 • а : 100 = 1,2а (грн) – ціна після підвищення;
1,2а грн — 100 %
х грн — 90 %
1,2а/х = 100/90; х = 1,2а • 90 : 100 = 1,08а (грн) – ціна після зниження.
а грн — 100 %
1,08а грн — х %
а/1,08а = 100/х; х = 1,08а • 100 : а = 108 (%)
108% – 100% = 8%
Відповідь: на 8% зросла початкова ціна.
Завдання 194
Ціну на товар спочатку знизили на 10 %, а через деякий час ще на 10 %. Чи такою самою стала б ціна цього товару, коли б її відразу знизили на 20 %?
Розв'язання
а грн — 100 %
х грн — 90 %
а/х = 100/90; х = 90 • а : 100 = 0,9а (грн) – ціна після зниження на 10%;
0,9а грн — 100 %
х грн — 90 %
0,9а/х = 100/90; х = 0,9а • 90 : 100 = 0,81а (грн) – ціна після зниження на 10%.
а грн — 100 %
х грн — 80 %
а/х = 100/80; х = а • 80 : 100 = 0,8а (грн) – ціна після зниження зразу на 20%.
0,81а > 0,8а
Відповідь: ні, ціна двох 10% знижок більша, ніж 20% знижка.
Завдання 195
Ціну на товар знизили на 20 %. На скільки відсотків треба підвищити нову ціну, щоб отримати її попереднє значення?
Розв'язання
а грн — 100 %
х грн — 80 %
а/х = 100/80; х = 80 • а : 100 = 0,8а (грн) – ціна після зниження на 20%.
0,8а грн — 100 %
а грн — х %
0,8а/а = 100/х; х = 100 • а : 0,8а = 125 (%)
125% – 100% = 25%
Відповідь: на 25%.
Завдання 196
Знайди два числа, середнє арифметичне яких менше від першого числа на 2 і менше від суми цих чисел на 3.
Розв'язання
Нехай сума двох чисел дорівнює х, тоді за умовою:
х - х/2 = 3
х/2 = 3
х = 3 • 2
х = 6
6 : 2 = 3 – середнє арифметичне цих чисел;
3 – 2 = 1 – перше число;
6 – 1 = 5 – друге число.
Відповідь: 1 і 5.
Завдання 197
Знайди площу фігури. Виміри подано в дециметрах.
4 • 2 + (5 – 3) • 6 + 3 • 4 = 8 + 12 + 12 = 32 (дм²)
Завдання 198
85 % співробітників міжнародної компанії знають англійську мову, а 75 % — німецьку. Скільки відсотків працівників знають обидві мови, якщо кожен знає хоча б одну?
Розв'язання
Розв'язання
1 спосіб
1) 100% – 85% = 15% – знають німецьку мову;
2) 75% – 15% = 60% – знають обидві мови.
2 спосіб
1) 85% + 75% = 160% – знають тільки німецьку мову і англійську мови;
2) 160% – 100% = 60% – знають обидві мови.
Відповідь: 60%.
Вправи для повторення
Завдання 199
На двох складах разом міститься 1400 т вугілля. Скільки вугілля на другому складі, якщо на першому його в 2,5 рази більше, ніж на другому?
Розв'язання
Нехай на другому складі х кг вугілля, тоді на першому складі 2,5х кг. Складаємо рівняння:
2,5х + х = 1400
3,5х = 1400
х = 1400 : 3,5
х = 400
Відповідь: на другому складі 400 т вугілля.
Завдання 200 Вирази
Якщо a = −8, b = −4, тоді |2а –3b| = |2 • (–8) – 3 • (–4)| = |–16 – (–12)| = |–4| = 4
Завдання 201
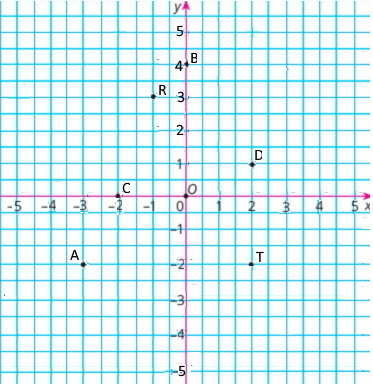
На координатній площині точки А(–3; –2), В(0; 4), С(–2; 0), D(2; 1), R(–1; 3), T(2; –2).