© ГДЗ 8next.com, 2013, 2018, 2022
Розв’язуємо усно
Завдання 1
1) 312 • 10 = 3120
2) 5 • 1000 = 5000
3) 100 • 10 000 = 1 000 000
4) 720 : 9 = 80
5) 480 : 4 = (400 + 80) : 4 = 400 : 4 + 80 : 4 = 100 + 20 = 120
6) 480 : 16 = 480 : (8 • 2) = 480 : 8 : 2 = 60 : 2 = 30
7) 1212 : 12 = (1200 + 12) : 12 = 1200 : 12 + 12 : 12 = 100 + 1 = 101
8) 1010 : 5 = (1000 + 10) : 5 = 1000 : 5 + 10 : 5 = 200 + 2 = 202
Завдання 2 Подвойте число 26. Знайдіть половину числа 26. Потройте число 27. Знайдіть третину числа 27.
26 • 2 = (20 + 6) • 2 = 20 • 2 + 6 • 2 = 40 + 12 = 52
26 : 2 = (20 + 6) : 2 = 20 : 2 + 6 : 2 = 10 + 3 = 13
27 • 3 = (20 + 7) • 3 = 20 • 3 + 7 • 3 = 60 + 21 = 81
27 : 3 = 9
Завдання 3 О 10 год ранку зі станції відправився поїзд зі швидкістю 60 км/год. На якій відстані від станції буде поїзд о 15 год того самого дня, якщо він рухатиметься з цією самою швидкістю і без зупинок?
Розв'язання:
1) 15 ─ 10 = 5 (год) ─ час у дорозі.
2) 60 • 5 = 300 (км) ─ буде відстань о 15 год.
Відповідь: о 15 год поїзд буде на відстані 300 км від станції.
Розв'язання: 60 • (15 ─ 10)= 300 (км)
Завдання 4 Мотузку розрізали на три частини так, що перша частина виявилася на 3 м коротшою від другої частини і на 3 м довшою за третю. На скільки метрів третя частина коротша від другої?
Розв'язання
Нехай х (м) ─ довжина першої частини мотузки, тоді х+3 (м) ─ довжина другої частини мотузки, а х—3 (м) ─ довжина третьої частини мотузки.
х + 3 ─ (х ─ 3) = х + 3 ─ х + 3 = 6 (м)
Відповідь: на 6 м третя частина мотузки коротша від другої..
Вправи
Вправа 92° Які з точок, зображених на рисунку 43, належать прямій a, а які не належать?
Розв'язання
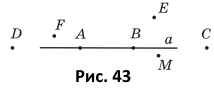
Належать: A, B, C, D
Вправа 93 Позначте в зошиті точки M і K та проведіть через них пряму. Позначте на відрізку MK точку N. Чи належить точка N прямій MK? Позначте на прямій MK точку P, яка лежить поза відрізком MK. Запишіть усі можливі позначення проведеної прямої.

Точка N належить прямій МК.
Позначення прямої: MN, NM, MK, KM, MP, PM, NK, KN, NP, PN, KP, PK
Вправа 94 Проведіть довільну пряму та позначте на ній точки А, В і С. Запишіть усі можливі позначення проведеної прямої.
Розв'язання
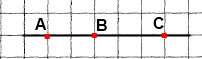
АВ, ВС, АС, ВА, СА
Вправа 95° Користуючись рисунком 44, установіть, чи є правильним твердження:
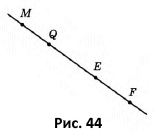
1) точка Q належить відрізку ME (правильне)
2) точка Q належить променю EF (неправильне)
3) точка Q належить променю FE (правильне)
4) точка Е належить променю MF і променю FM (правильне)
5) точка М належить відрізку QE (неправильне)
6) точка М належить прямій QE (правильне)
Вправа 96 Накресліть промінь OA та відкладіть на ньому 1 см.
![]()
Чи можна на цьому промені відкласти 100 таких відрізків? Можна відкласти довільну кількість відрізків, бо промінь має початок, але не має кінця.
Вправа 97° Чи перетинаються зображені на рисунку 45?
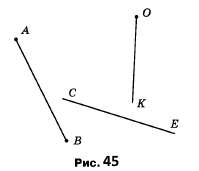
1) пряма СЕ і відрізок АВ (так)
2) промінь ОК і пряма СЕ (так)
3) промінь ОК і відрізок АВ (ні)
Вправа 98° Чи перетинаються зображені на рисунку 46?
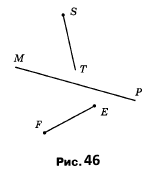
1) пряма МР і відрізок EF (ні)
2) промінь ST і пряма МР (так)
3) відрізок EF і промінь ST (так)
Вправа 99° Позначте в зошиті:
1) чотири точки, жодні три з яких не лежать на одній прямій; 2) п’ять точок, жодні три з яких не лежать на одній прямій.
Розв'язання
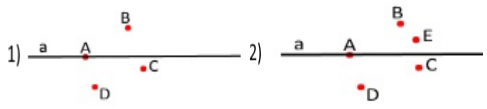
Вправа 100° На прямій АВ позначено дві точки М і N. Назвіть фігури, які утворилися при цьому.
Розв'язання
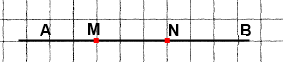
Промені: MA, MN, MB, NA, NM, NB
Відрізки: MN
Вправа 101* Назвіть усі відрізки, прямі та промені, зображені на рисунку 47.
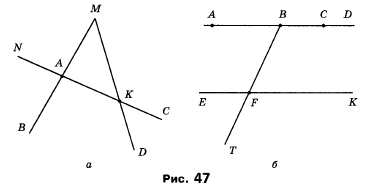
Розв'язання
а) прямі NC, AK; промені MA, MB, MK, MD, AB, AN, AC, KN, KD, KC; відрізки AK, AM, KM
в) прямі AD, BD, CD, EK; промені AD, BD, CD, BT, FE, FK, FT; відрізки AB, AC, BC, BF
Вправа 102 Назвіть усі відрізки, прямі та промені, зображені на рисунку 48.
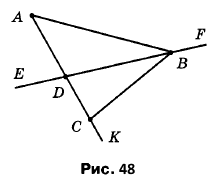
Розв'язання
Прямі EF
Промені DE, DF, DK, AK, CK, BE, BF
Відрізки AD, AC, AB, BD, BC, DF, DC
Вправа 103 Накресліть два промені так, щоб їх спільна частина була 1) точкою; 2) відрізком (спільна частина); 3) променем (спільна частина).
Розв'язання
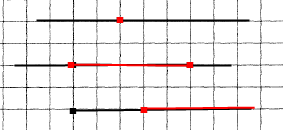
Вправа 104 Позначте на площині точки М, К, Т і F так, щоб промінь МК перетинав пряму ТF, а промінь ТF не перетинав пряму МК.
Розв'язання
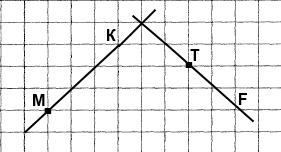
Вправа 105 Скільки променів утвориться, якщо на прямій позначити:
1) 4 точки; 2) 100 точок?
З кожної точки на прямій можуть виходити два промені в протилежних напрямках, тому променів буде удвічі більше від кількості точок на прямій.
1) 4 • 2 = 8 променів.
2) 100 • 2 = 200 променів.
Вправа 106 Точки А, В і С лежать на одній прямій. Знайдіть довжину відрізка ВС, якщо АВ = 24 см, АС = 32 см. Скільки розв’язків має задача?
Розв'язання
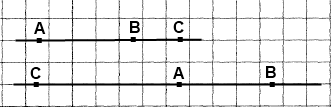
ВС = АС ─ АВ = 32 см ─ 24 см = 8 см
ВС = АС + АВ = 32 см + 24 см = 56 см
Задача має два розв'язки.
Вправа 107 Точки М, К i N лежать на одній прямій. Знайдіть довжину відрізка KN, якщо МК = 15 см, MN = 6 см.
Розв'язання
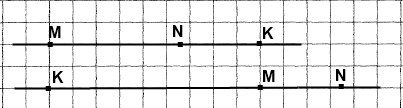
КN = МК ─ МN = 15 см ─ 6 см = 9 см
КN = МК + МN = 15 см + 6 см = 21 см
Вправа 108 На площині проведено п’ять прямих, що попарно перетинаються. Яка найменша можлива кількість точок перетину цих прямих? Яка найбільша кількість точок перетину може бути?
Розв'язання
Найменша кількість точок перетину п'яти прямих — 1, найбільша — 10.
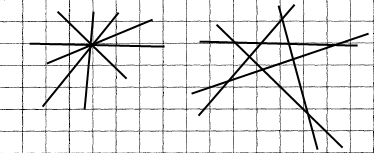
Вправа 109 На площині проведено три прямі. На яку найбільшу і на яку найменшу кількість частин ці прямі можуть розбити площину?
Розв'язання
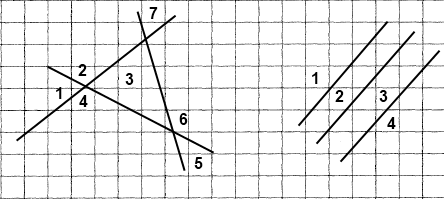
Найбільша кількість частин — 7, найменша — 4
Вправи для повторення
Вправа 110 У парку росте 168 дубів, беріз — у 4 рази менше, ніж дубів, а кленів — на 37 дерев більше, ніж беріз. Скільки всього дубів, беріз і кленів росте в парку?
Короткий запис
Дубів — 168 д.
Беріз — ?, у 4 рази менше, ніж дубів
Кленів — ?, на 37 д. більше, ніж беріз
Розв'язання
1) 168 : 4 = (160 + 8) : 4 = 42 (д.) ─ беріз росте;
2) 42 + 37 = 79 (д.) ─ кленів росте;
3) 168 + 42 + 79 = 289 (д.) ─ всього дерев в парку.
Відповідь: у парку росте 289 дубів, беріз і кленів.
Вправа 111 Група туристів пройшла пішки 72 км, проїхала поїздом у 5 разів більше, ніж пройшла пішки, а автобусом проїхала на 128 км менше, ніж поїздом. Скільки всього кілометрів подолали туристи?
Короткий запис
Пішки — 72 км
Поїздом — ?, у 5 разів більше, ніж пішки
Автобусом — ?, на 128 км менше, ніж поіздом
Усього — ?
Розв'язання
1) 72 • 5 = (70 + 2) • 5 = 360 (км) ─ відстань проїхала поїздом;
2) 360 ─ 128 = 232 (км) ─ відстань проїхала автобусом;
3) 72 + 360 + 232 = 664 (км) ─ уся відстань.
Відповідь: туристи подолали 664 км.
Вправа 112 Відправившись у гості до Івасика Телесика, Баба—Яга пролетіла у своїй ступі 276 км за 4 год, а решту 156 км пройшла за 6 год у чоботах—скороходах. На скільки швидкість ступи більша за швидкість чобіт—скороходів?
|
|
Швидкість |
Час |
Відстань |
|
|
У ступі |
? |
На ?
|
4 год |
276 км |
|
У чоботах-скороходах |
? |
6 год |
156 км |
|
Розв'язання
1) 276 : 4 = (240 + 36) : 4 = 69 (км/год) ─ швидкість ступи;
2) 156 : 6 = (120 + 36) : 6 = 26 (км/год) ─ швидкість чобіт—скороходів;
3) 69 ─ 26 = 43 (км/год) ─ на стільки швидкість ступи більша, ніж чобіт—скороходів.
Відповідь: швидкість ступи на 43 км/год більша за швидкість чобіт—скороходів.
Вправа 113 За течією річки човен пропливає 95 км за 5 год, а проти течії — 119 км за 7 год. На скільки швидкість човна проти течії менша від його швидкості за течією?
|
|
Швидкість |
Час |
Відстань |
|
|
За течією |
? |
На ?
|
5 год |
95 км |
|
Проти течії |
? |
7 год |
119 км |
|
Розв'язання
1) 95 : 5 = (50 + 45) : 5 = 19 (км/год) ─ швидкість за течією річки.
2) 119 : 7 = (70 + 49) : 7 = 17 (км/год) ─ швидкість проти течії річки.
3) 19 ─ 17 = 2 (км/год) ─ на стільки швидкість проти течії менша, ніж швидкість за течією річки.
Відповідь: швидкість проти течії річки на 2 км/год менша від швидкості за течією.
Вправа 114 На прямій позначили 20 точок так, що відстань між будь—якими двома сусідніми точками дорівнює 4 см. Знайдіть відстань між крайніми точками.
Розв'язання
Міркуємо так: 20 точок утворюють 19 відрізків довжиною по 4 см.
4 • (20 ─ 1) = 4 • 19 = 4 • (9 + 10) = 76 (см) — відстань між крайніми точками.
Відповідь: 76 см.
Вправа 115 На прямій позначили точки так, що відстань між будь—якими двома сусідніми точками дорівнює 5 см, а між крайніми точками — 45 см. Скільки точок було позначено на прямій?
Розв'язання
1) 45 : 5 = 9 (в.) — відрізків позначено.
2) 9 + 1 = 10 (т.) — точок позначено.
Відповідь: на прямій було позначено 10 точок.
Задача від Мудрої Сови
Вправа 116 Як вишикувати 16 учнів у три ряди, щоб у кожному ряду їх було порівну?
Розв'язання