© ГДЗ 8next.com, 2013, 2018, 2022
Запитання
1. Який кут називають розгорнутим? Кут, сторони якого утворюють пряму, називають розгорнутим.
2. У яких одиницях вимірюють кути? Величину одиниці виміру кута називають градусом (від лат. gradus — ≪крок≫, ≪сходинка≫) і записують 1°.
3. Яка градусна міра розгорнутого кута? 180°.
4. Як називають прилад, що використовують для вимірювання кутів? Транспортир.
5. Які градусні міри мають рівні кути? Рівні кути мають рівні градусні міри.
6. Який із двох нерівних кутів уважають більшим? Із двох нерівних кутів більшим будемо вважати той, градусна міра якого більша.
7. Яку властивість має величина кута? Якщо між сторонами кута ABC провести промінь BD, то градусна міра кута ABC дорівнюватиме
сумі градусних мір кутів ABD и DBC, тобто ∠ABC = ∠ABD + ∠DBC.
8. Який кут називають прямим? Кут , градусна міра якого дорівнює 90°, називають прямим.
9. Який кут називають гострим? Кут, градусна міра якого менша від 90°, називають гострим.
10. Який кут називають тупим? Кут, градусна міра якого більша за 90°, але менша від 180°, називають тупим.
Розв’язуємо усно
Завдання 1 Назвіть два числа, одне з яких:
1) на 27 більше за друге (30 ‒ 3 = 27)
2) на 15 менше від другого (45 ‒ 30 = 15)
3) у 7 разів менше від другого (42 : 6 = 7)
4) у 3 рази більше за друге (21 : 7 = 3)
Завдання 2 Годинник спішить на 10 хв і зараз показує 10 год 8 хв. Яка година насправді?
Розв'язання
10 год 08 хв ‒ 10 хв = 9 год 68 хв ‒ 10 хв = 9 год + (68 хв ‒ 10 хв) =
= 9 год 58 хв ‒ година насправді.
Завдання 3 Годинник відстає на 7 хв і зараз показує 16 год 55 хв. Яка година насправді?
Розв'язання
16 год 55 хв + 7 хв = 16 год + 62 хв = 17 год 2 хв ‒ година насправді.
Завдання 4 Для озеленення вулиці завдовжки 3 км на одному її боці посадили дерева на відстані 20 м одне від одного. Скільки дерев було посаджено? Чому дорівнює відстань між першим і п’ятим деревами?
Розв'язання
3 км = 3000 м
1) 3000 : 20 = 150 (в.) ‒ між деревами на вулиці.
2) 150 + 1 = 151 (д.) ‒ дерев посаджено.
3) 5 ‒ 1 = 4 (в.) ‒ між першим і п’ятим деревами.
4) 20 • 4 = 80 (м.) ‒ між першим і п’ятим деревами.
Відповідь: посаджено 150 дерев, відстань між першим і п’ятим деревами дорівнює 80 м.
Вправи
Вправа 317° Знайдіть на рисунку 103 гострі, тупі та прямі кути.
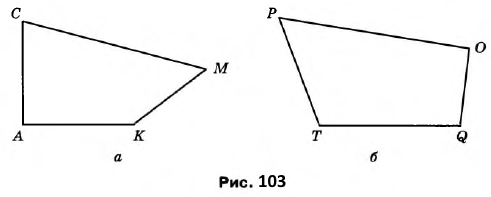
Розв'язання
|
а) Прямий ∠А Гострі ∠С, ∠М Тупий ∠К |
б) Прямий ∠О Гострий ∠Р Тупі ∠Т, ∠Q |
Вправа 318° Які з даних кутів гострі, тупі, прямі, розгорнуті: ∠A = 96°, ∠B = 84°, ∠S = 180°, ∠D = 90°, ∠R = 162°, ∠E = 60°, ∠Q = 100°, ∠M = 72°?
Розв'язання
Гострі кути: ∠B = 84°, ∠E = 60°, ∠M = 72°
Тупі кути: ∠A = 96°, ∠R = 162°, ∠Q = 100°
Прямі кути: ∠D = 90°
Розгорнуті кути: ∠S = 180°
Вправа 319° Градусна міра кута між бісектрисою даного кута та його стороною?
|
1) 24°; 12° |
2) 170°. 85° |
Вправа 320° Знайдіть градусну міру кута, бісектриса якого утворює з однією з його сторін кут, що дорівнює:
|
1) 37°; 74° |
2) 75°. 150° |
Вправа 321° Визначте за рисунком 104 градусну міру кута:
Вправа 322° Знайдіть, користуючись транспортиром, градусну міру кутів, зображених на рисунку 105. Визначте вид кожного кута.
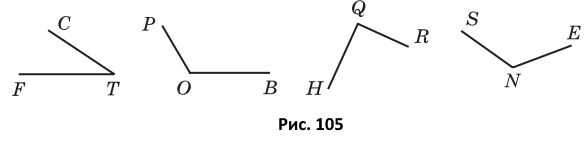
Розв'язання
∠АМК = 30° (гострий кут); <BOP = 120° (тупий кут);
∠HQR = 90° (прямий кут); <SNE = 125° (тупий кут);
Вправа 323° Знайдіть, користуючись транспортиром, градусну міру кутів, зображених на рисунку 106. Визначте вид кожного кута.
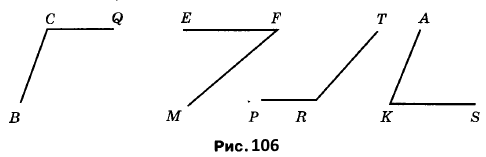
Розв'язання
∠BCQ = 110° (тупий кут); ∠EFM = 40° (гострий кут); ∠PRT = 130° (тупий кут); ∠AKS = 70° (гострий кут)
Вправа 324° Накресліть: 1) гострий кут EFC; 2) прямий кут ORT; 3) тупий кут D; 4) розгорнутий кут КАР.
Розв'язання

Вправа 325° Накресліть кут, градусна міра якого дорівнює:
1) 38°; 2) 124°; 3) 92°; 4) 90°; 5) 87°; 6) 54°; 7) 170°. Визначте вид кожного кута.
Розв'язання
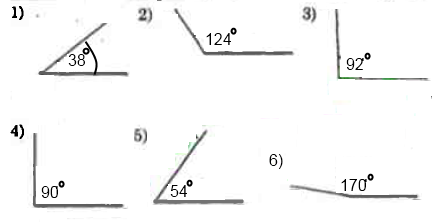
Гострі кути 1) 38°, 5) 54°.
Тупі кути 2) 124°, 3) 92°, 6) 170°.
Прямий кут 4) 90°.
Вправа 326 Проведіть промінь. Відкладіть від цього променя кут, градусна міра якого дорівнює: 1) 40°; 2) 130°; 3) 68°; 4) 164°. Визначте вид кожного з побудованих кутів.
Розв'язання
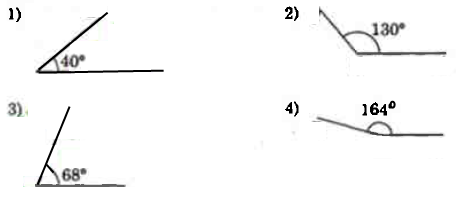
Гострі кути 1) 40°; 3) 68°. Тупі кути 2) 130°; 4) 164°.
Вправа 327° (Домашня практична робота) Візьміть аркуш паперу формату А4. Згинаючи цей аркуш, побудуйте бісектриси його кутів. Не користуючись транспортиром, визначте градусні міри кутів, які утворилися. Оскільки аркуш А4 є прямокутником, то відповідно усі його кути дорівнюють 90°. Бісектриса ділить будь-який кут навпіл, тому утворені кути матимуть 45° (90° : 2 = 45°).
Вправа 328° На рисунку 107 <CMK = 132°, а кут АМК — розгорнутий. Обчисліть величину кута АМС.
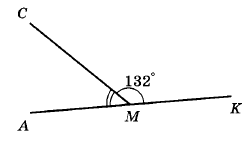
Відомо: ∠CMK = 132°, ∠АМК=180°. Знайти: ∠AMC -?
Розв'язання
∠АМС = ∠АМК ‒ ∠СМК = 180° ‒ 132° = 48°
Вправа 329 На рисунку 108 кут АОК — прямий, <COP = 54°, а кут СОК — розгорнутий. Обчисліть величину кута АОР.
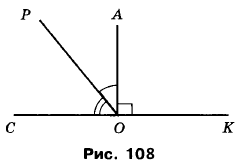
Відомо: ∠AOK = 90°, ∠COP = 54°, ∠COK = 180°
Знайти: ∠AOP - ?
Розв'язання
∠АОР = ∠СОК ‒ ∠АОК ‒ ∠СОР = 180° ‒ 90° ‒ 54° = 36°
Вправа 330° Який із кутів, зображених на рисунку 109, найбільший? найменший?
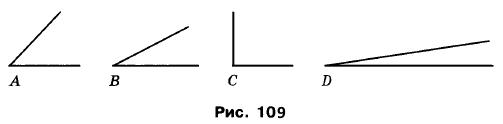
Розв'язання
Найбільший ∠С, найменший ∠D.
Вправа 331 Накресліть кут CDE, який дорівнює 152°. Променем DA розділіть його на два кути так, щоб <CDA = 98°. Обчисліть величину кута ADE.
Розв'язання
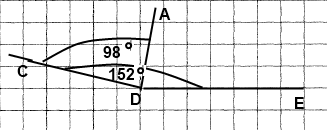
Відомо: ∠СDE = 152°, ∠CDA = 98°
Знайти: ∠ADE - ?
Розв'язання
∠АDЕ = ∠СDЕ ‒ ∠СDА = 152° ‒ 98° = 54°
Вправа 332 Накресліть кут ABC, який дорівнює 106°. Променем BD розділіть цей кут на два кути так, щоб <ABD = 34°. Обчисліть величину кута DBC.
Розв'язання
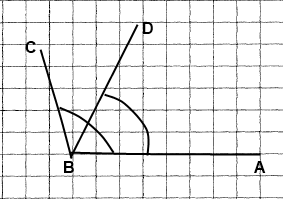
Відомо: ∠ABC = 106°, ∠ABD = 34°
Знайти: ∠DBC - ?
Розв'язання
∠DВС = ∠АВС ‒ ∠АВD = 106° ‒ 34° = 72°
Вправа 333 3 вершини прямого кута ВОМ (рис. 110) проведено промені ОА і ОС так, що <BOC = 74°, <AOM = 62°. Обчисліть величину кута АОС.
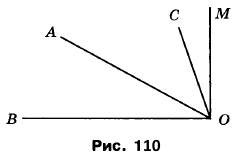
Відомо: ∠BOM = 90°, ∠BOC = 74°, ∠AOM = 62°
Знайти: ∠AOC - ?
Розв'язання:
∠СОМ = ∠ВОМ ‒ ∠ВОС = 90° ‒ 74° = 16°
∠АОС = ∠АОМ ‒ ∠СОМ = 62° ‒ 16° = 46°
Вправа 334 З вершини розгорнутого кута АСР (рис. 111) проведено промені СТ і CF так, що <ACF = 158°, <TCP = 134°. Обчисліть величину кута TCF.
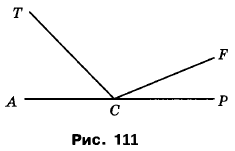
Відомо: ∠ACP = 180°, ∠ACF = 158°, ∠TCP = 134°
Знайти: ∠TCF - ?
Розв'язання
∠FCP = ∠ACP ‒ ∠ACF = 180° ‒ 158° = 22°
∠TCF = ∠TCP ‒ ∠FCP = 134° ‒ 22° = 112°
Вправа 335* Чи правильне твердження:
1) будь‒який кут, менший від тупого, — гострий (ні, прямий кут теж менший від тупого кута);
2) кут, менший від розгорнутого, — тупий (ні, гострий і прямий кути теж менші від розгорнутого кута);
3) бісектриса тупого кута ділить його на два гострих кути (так, тупий кут менший від 180°, тому бісектриса ділить його на два рівні кути, кожен з яких є меншим від 90°);
4) сума градусних мір двох гострих кутів більша за 90° (ні, наприклад, 10° + 20° < 90°);
5) кут, більший за прямий, — тупий (ні, розгорнутий кут більший за прямий).
Вправа 336 Знайдіть градусну міру кута між стрілками годинника,
якщо вони показують:
1) 3 год; 30° • 3 = 90°
2) 6 год; 30° • 6 = 180°
3) 4 год; 30° • 4 = 120°
4) 11 год; 30° • 1 = 30°
5) 7 год. 30° • 5 = 150°
Вправа 337 Проведіть три прямі, що перетинаються в одній точці. Запишіть усі розгорнуті кути, які утворилися при цьому.
Розв'язання
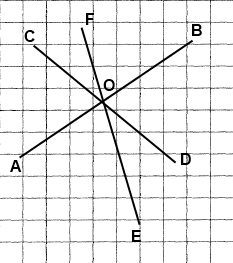
Розгорнуті кути: ∠AOB, ∠FOE, ∠COD
Вправа 338 Накресліть кут ABC, градусна міра якого становить 120°. Проведіть промінь BD так, щоб градусна міра кута ABD дорівнювала 40°. Обчисліть градусну міру кута DBC.
Відомо: ∠AВC = 120°, ∠ABD = 40°
Знайти: ∠DBC - ?
Розв'язання
∠DBC = ∠ABC‒ ∠АВD = 120° ‒ 40° = 80°
∠DBC = ∠ABD + ∠АBC = 40° + 120° = 160°
Скільки розв’язків має задача? Два розв'язки.
Вправа 339 Промінь ВК є бісектрисою кута CBD, <ABK = 146° (рис. 112). Обчисліть градусну міру кута CBD.
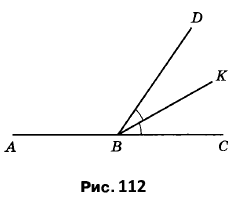
Відомо: ∠AВК = 146°, ∠СВК = ∠КВD
Знайти: ∠CBD - ?
Розв'язання
∠СВК = ∠АВС ‒ ∠АВК = 180° ‒ 146° = 34°
∠СВD = 2 • ∠СВК = 2 • 34° = 68°
Вправа 340* Промінь ОА є бісектрисою кута СОМ, <COM = 54° (рис. 106). Обчисліть градусну міру кута АОВ.
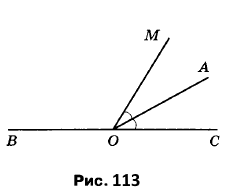
Відомо: ∠COM = 54°, ∠COA = ∠AOM
Знайти: ∠AOB - ?
Розв'язання
∠АОМ = ∠СОМ : 2 = 54° : 2 = 27°
∠ВОМ = ∠ВОС ‒ ∠СОМ = 180° ‒ 54° = 126°
∠АОВ = ∠АОМ + ∠ВОМ = 27° + 126° = 153°
Вправа 341
Як, використовуючи шаблон кута, градусна міра якого дорівнює 13°, побудувати кут, градусна міра якого дорівнює 2°?
Розв’язання
1) 13° • 14 – 180° = 182° – 180° = 2°
Провести лінію, зліва направо відкласти 14 разів даний кут. Кут під лінією буде шуканим.
Вправа 342
Як побудувати кут, градусна міра якого 1°, використовуючи шаблон кута, градусна міра якого дорівнює: 19°?
Розв’язання
19° • 19 – 360° = 361° – 360° = 1°
Провести лінію, справа наліво відкласти 19 разів даний кут. Кут над лінією буде шуканим.
Як побудувати кут, градусна міра якого 1°, використовуючи шаблон кута, градусна міра якого дорівнює 7°?
Розв’язання
7° • 13 – 90° = 91° – 90° = 1°
Провести лінію та перпендикуляр до неї, справа наліво відкласти 13 разів даний кут. Кут за перпендикуляром буде шуканим.
Вправи для повторення
Завдання 343 Заповніть ланцюжок обчислень:
Розв'язання
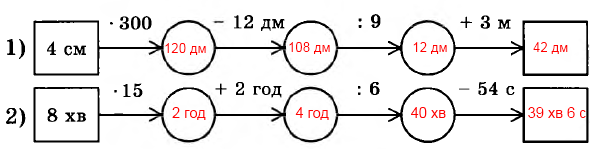
1) 4 см • 300 = 1200 см = 120 дм
120 дм ‒ 12 дм = 108 дм
108 дм : 9 = (90 дм + 18 дм) : 9 = 10 дм + 2 дм = 12 дм
12 дм + 3 м = 12 дм + 30 дм = 42 дм
2) 8 хв • 15 = (10 + 5) • 8 хв = 80 хв + 40 хв = 120 хв = 2 год
2 год + 2 год = 4 год
4 год : 6 = (4 • 60 хв) : 6 = 240 хв : 6 = 40 хв
40 хв ‒ 54 с = 39 хв + 1 хв ‒ 54 с = 39 хв + 60 с ‒ 54 с = 39 хв 6 с
Вправа 344 У чотирьох стаканах вміщується стільки ж молока, як і в банці. У стакані та банці вміщується разом 1 кг 200 г молока. Скільки грамів молока вміщується у стакані?
Розв'язання
1 кг 200 г = 1200 г
Якщо в 1 банці уміщується 4 стакани молока, тоді 1200 г молока уміщується в 5 стаканах, тоді
1200 : 5 = 240 (г) ‒ молока в 1 стакані.
Відповідь: у стакані вміщується 240 г молока.
Учимося застосовувати математику
Вправа 345 Мати дала Андрійкові 300 грн і доручила купити банани, мандарини й апельсини. Андрійко вирішив купити 3 кг бананів по 42 грн за 1 кг, 2 кг мандаринів по 51 грн і 1 кг апельсинів по 45 грн. Чи вистачить йому на це грошей? У разі позитивної відповіді вкажіть, скільки грошей у нього залишиться.
Розв’язання
1) 42 • 3 = 126 (грн) ‒ заплатив за банани.
2) 51 • 2 = 102 (грн) ‒заплатив за мандарини.
3) 126 + 102 + 45 = 273 (грн) ‒ заплатив за покупку.
273 < 300
4) 300 ‒ 273 = 27 (грн)
Відповідь: так, вистачить грошей на покупку; в Андрійка залишиться 27 гривень решта.
Вправа 346 На ХХХІ Олімпійських іграх, що відбулися у 2016 р. у Ріо-де-Жанейро (Бразилія), олімпійська збірна України здобула 11 медалей. Наші спортсмени отримали 7 золотих і срібних медалей, а золотих і бронзових — 9. Скільки медалей кожного виду завоювювала на цій олімпіаді наша зб
Розв’язання
1) 11 ‒ 7 = 4 (м.) ‒ бронзових медалей.
2) 9 ‒ 4 = 5 (м.) ‒ золотих медалей.
3) 7 ‒ 5 = 2 (м.) ‒ срібних деталей.
Відповідь: 4 бронзових медалей, 5 золотих медалей, 2 срібних медалей.
Вправа 347
Прокат човна коштує 24 грн за першу годину або її частину. Кожна наступна година прокату або її частина коштує 18 грн. Василь узяв човна о 9 год 40 хв, а повернув о 13 год 15 хв того самого дня. Скільки заплатив Василь за прокат човна?
Розв’язання
13 год 15 хв ‒ 9 год 40 хв = 12 год 75 хв ‒ 9 год 40 хв = 3 год 35 хв – час прокату човна. 3 год 35 хв = 1 год + (2 год + 35 хв)
24 + 18 • 3 = 24 + 54 = 78 (грн)
Відповідь: 78 гривнів заплатив Василь за прокат човна.
Задача від Мудрої Сови.
Вправа 348 Равлик удень піднімається вгору по жердині на З м, а вночі з’їжджає по ній на 2 м вниз. На який день він добереться до вершини жердини, довжина якої дорівнює 20 м?
Розв'язання
1) 3 ‒ 2 = 1 (м) ‒ відстань за 1 день.
За 17 днів равлик підніметься на 17 м, на 18 день підніметься ще на 3 м, тоді досягне позначку 20 м.
Відповідь: равлик добереться вершини на 18 день.
------------------------------ у підручнику за 2013, 2018 рік ----------------------------
Запитання
6. Розкажіть, як користуватися транспортиром. Щоб виміряти кут, сумістимо його вершину з центром транспортира так, щоб одна із сторін кута пройшла по лінійці, тоді штрих на шкалі, через який пройде друга сторона, укаже градусну міру (величину) цього кута.
13. На які кути ділить розгорнутий кут його бісектриса? Бісектриса розгорнутого кута ділить його на два кути, градусна міра кожного з яких дорівнює 90°
14. У яких випадках говорять, що від даного променя відкладено даний кут? Якщо дано промінь ОА і побудовано кут ВОА, то говорять, що від променя ОА відкладено кут ВОА.
Розв’язуємо усно
Завдання 4 Які з даних рівнянь не мають коренів: 1), 4), 6)
Врава 323. Довжина сухопутного кордону України з Росією, Білоруссю та Молдовою становить 4232 км. Знайдіть довжину кордону України з кожною з цих держав, якщо довжина кордону з Росією і Білоруссю дорівнює 3038 км, а з Росією і Молдовою — 3257 км.
Розв'язання.
1) 4232 ‒ 3038 = 1194 (км) ‒ довжина кордону з Молдовою.
2) 3257 ‒ 1194 = 2063 (км) ‒ довжина кордону з Росією.
3) 3038 ‒ 2063 = 975 (км) ‒ довжина кордону з Білорусією.
Відповідь: довжина кордону з Білорусією 975 км, Молдовою ‒ 1194 км, Росією ‒ 2063 км.
Вправа 318* Проведіть шість прямих, що перетинаються в одній точці. Чи правильно, що серед кутів, які при цьому утворилися, є кут, градусна міра якого менша від 31°?
Розв'язання
180° : 6 = 30°
Так.
Вправа 322 Чи правильна нерівність (а + 253) • 7 < (9864 ‒ а) : 4 при а = 124?
Розв'язання
Якщо а = 124, тоді (а + 253) • 7 = (124 + 253) • 7 = 377 • 7 = 2639
Якщо а = 124, тоді (9864 ‒ а) : 4 = (9864 ‒ 124) : 4 = 9740 : 4 = 2435
2639 > 2435
Відповідь: нерівність неправильна.
Завдання 324
Прокат човна коштує 16 грн за першу годину або її частину. Кожна наступна година прокату або її частина коштує 12 грн. Василь узяв човна о 9 год 40 хв, а повернув о 13 год 15 хв того самого дня. Скільки заплатив Василь за прокат човна?
Розв’язання
13 год 15 хв – 9 год 40 хв = 12 год 75 хв – 9 год 40 хв = 3 год 35 хв – час прокату човна. 3 год 35 хв = 1 год + (2 год + 35 хв)
16 + 12 • 3 = 16 + 36 = 52 (грн) – заплатив Василь за прокат човна.
Відповідь: 52 гривні заплатив Василь за прокат човна.